Transformer 原理解析:从注意力机制到自回归生成
概述
框架
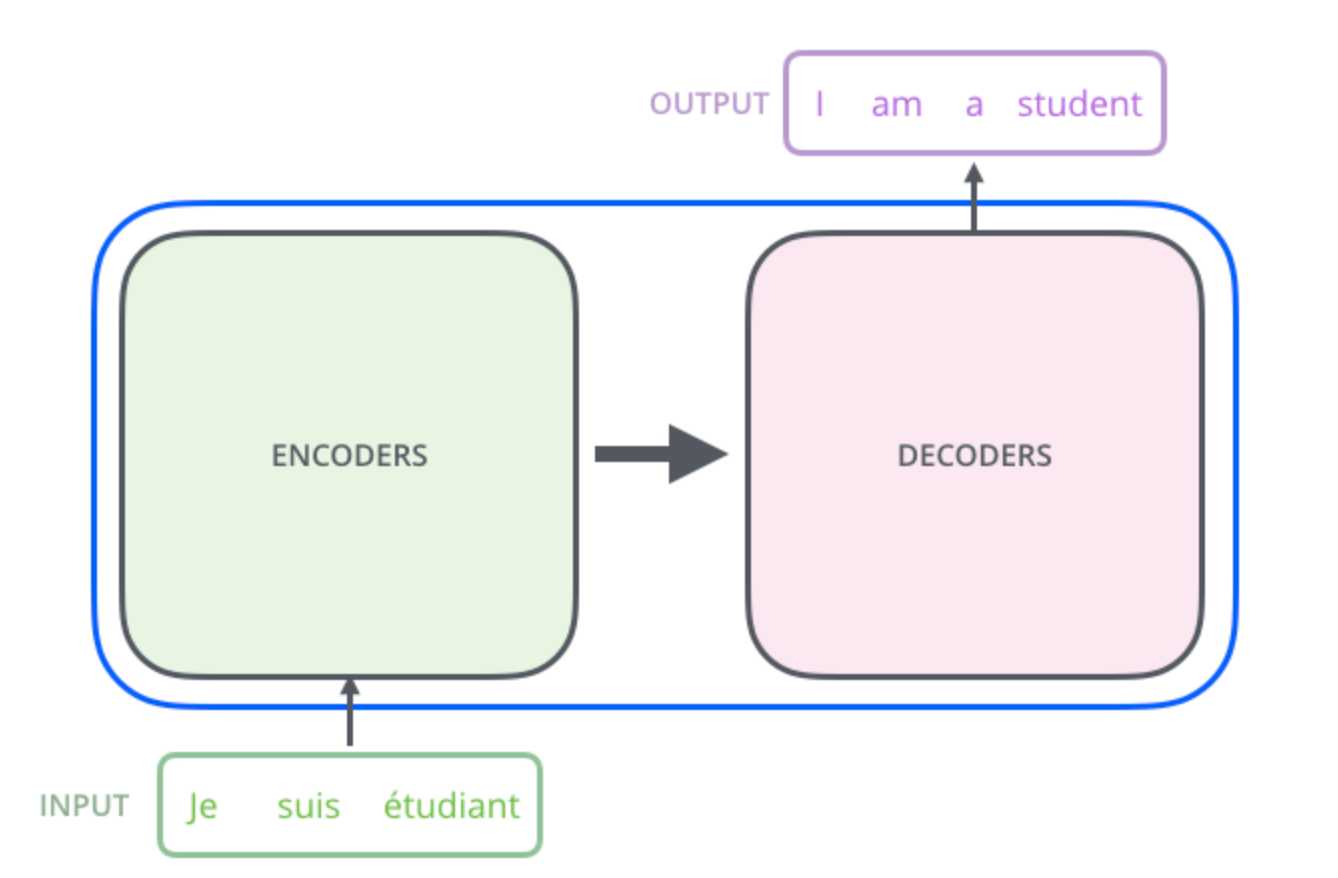
以翻译作为例子,从宏观角度理解大模型,可以把大模型视为一个黑匣子,它可以输入一种语言然后输出另外一种翻译语言,如下图所示。
如果将模型稍微展开一下,模型分为encoders和decoders两部分。为什么要分为编码器和解码器了?主要是从以下动机考量。
- 条件生成需求:在机器翻译、摘要、对话等条件文本生成任务重,需要读懂输入再逐步输出目标序列这两个事情的约束不同。读懂输入需要双上下文(每个词即要看到左也要右),也就是说要在上下文中去理解,没有因果约束。而生成输出需要的是自回归,因为是预测,只需要看历史不能偷看未来,这就需要因果掩码的自注意力。
- 结构解耦:把理解和生成拆开,分别最优各自的注意力、掩码和结构,这样更清晰也更高效。
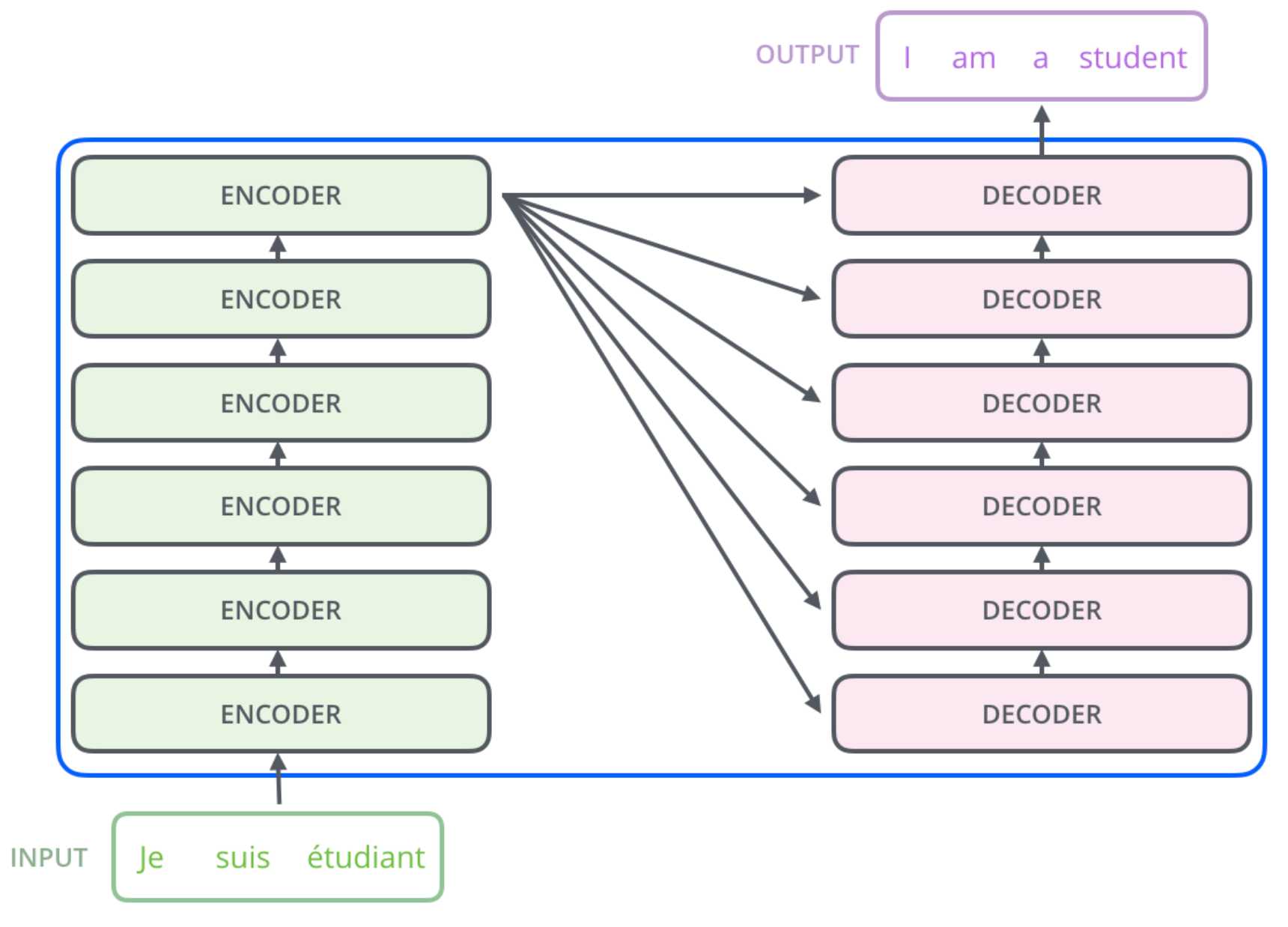
encoders是有多个相同的encoder堆叠在一起形成,decoders也是一样。
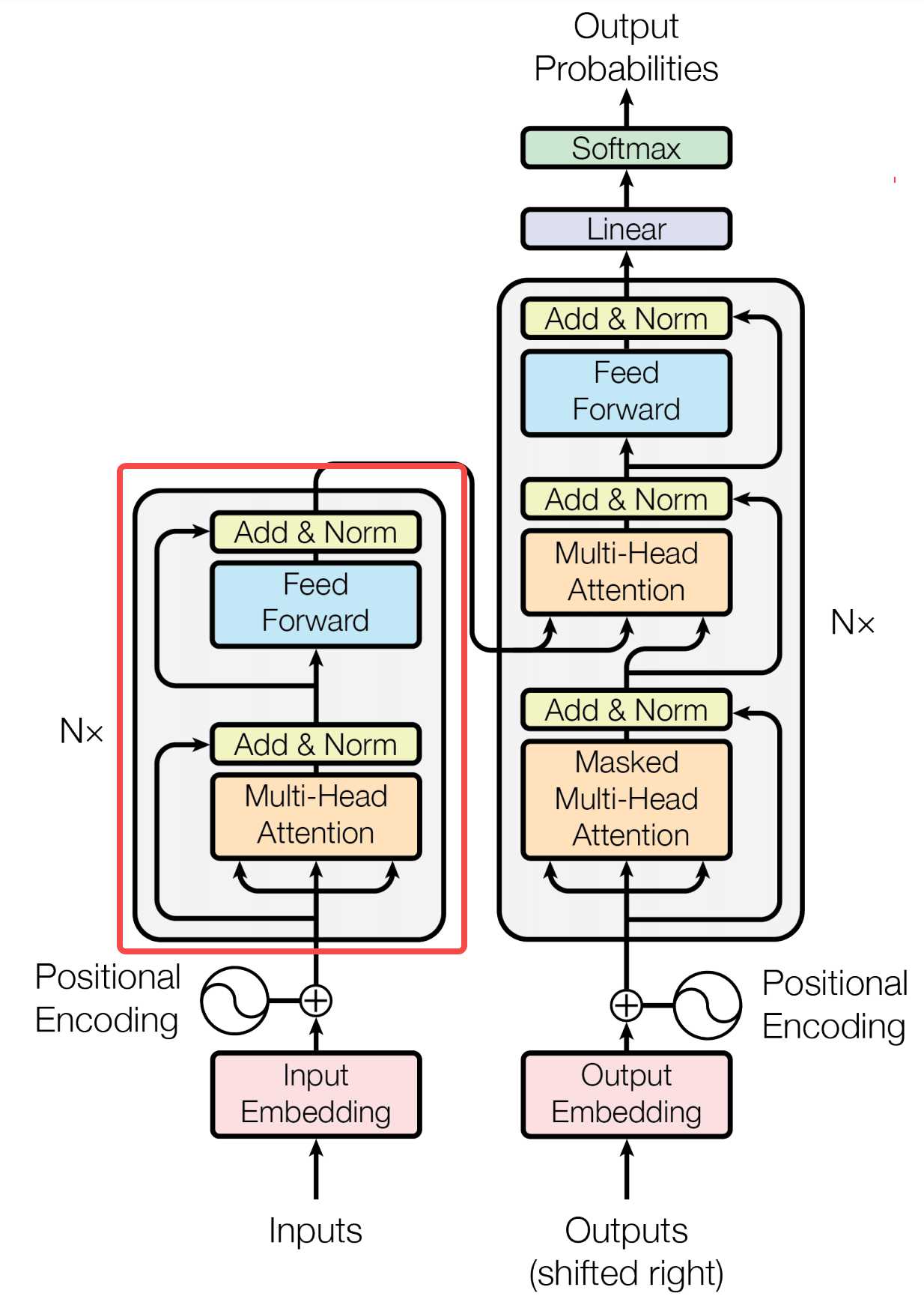
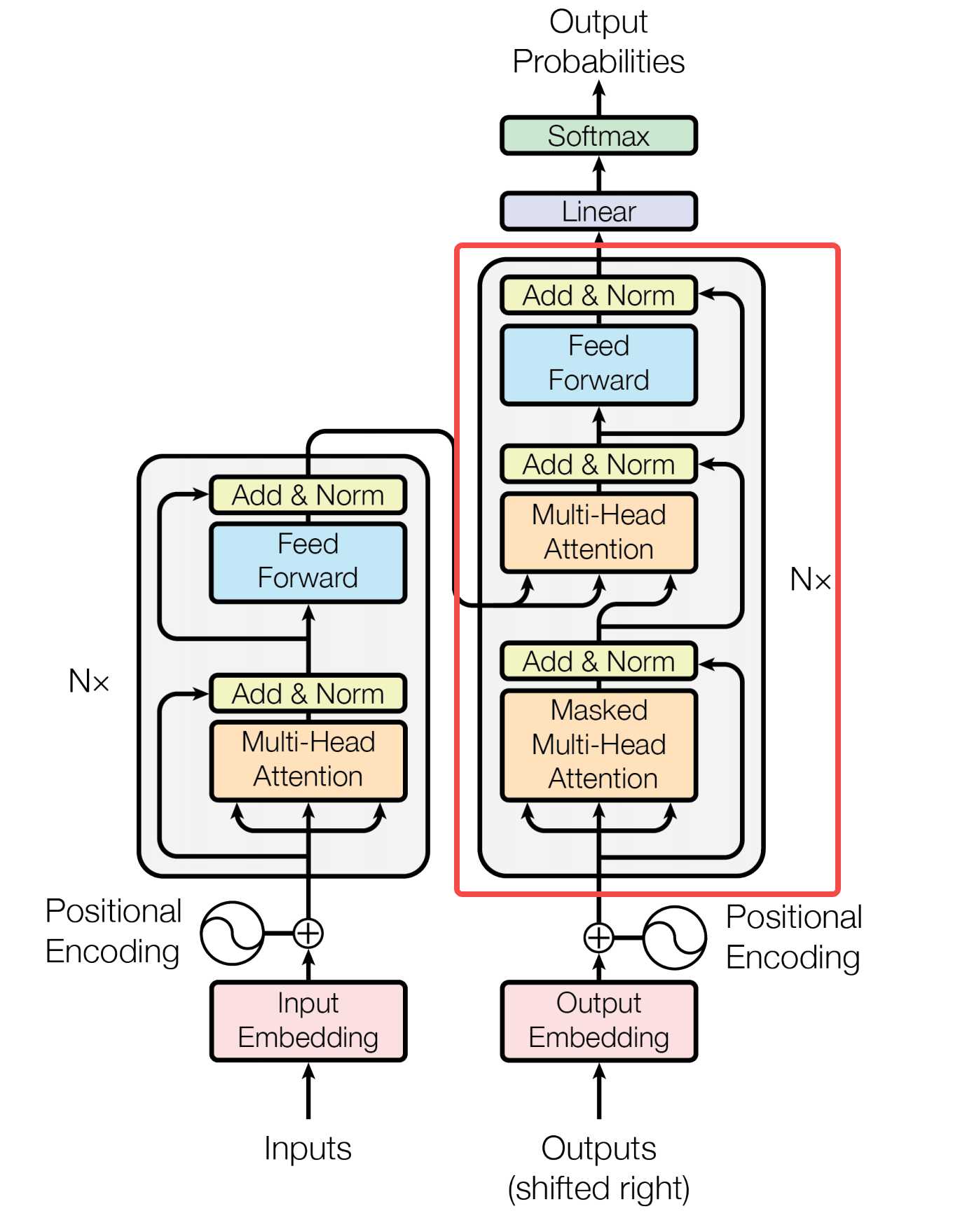
encoder和decoder在结构上都是相同的,但是他们不共享权重。下图是encoder和decoder微观结构。
编码器将输入的序列X=(x1,……,xn)映射到连续表示序列Z=(z1,…..zn),然后将Z给到解码器。解码器每次生成一个元素的符号输出序列(y1,……yn)。解码器在每一步都是自回归的,在生成下一步时将先前生成的符号作为额外输入。
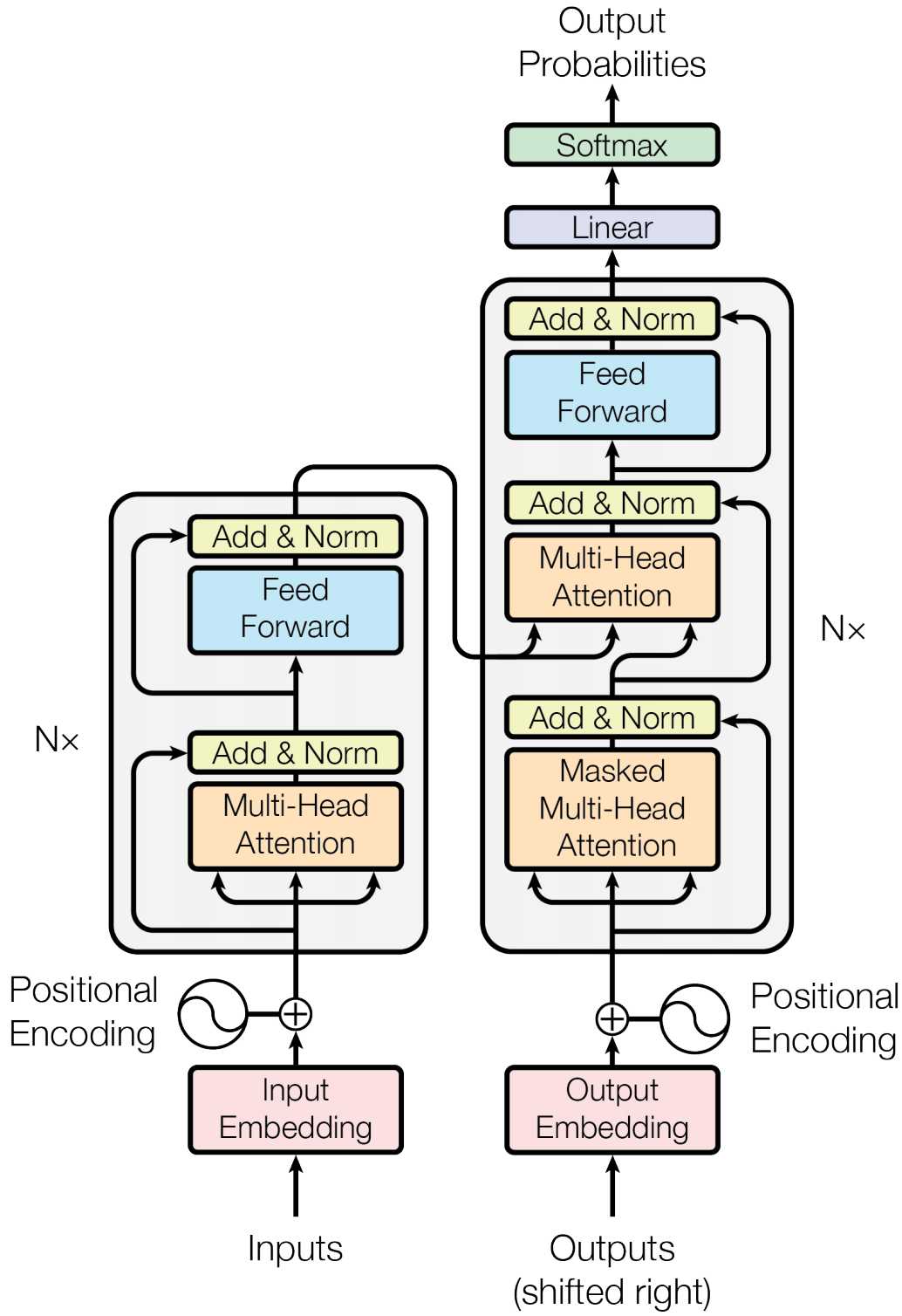
- 编码器:编码器由N=6个相同层堆叠组成。每层都有两个子层,第一个子层是多头注意力(Multi-Head Attention),第二个是简单的按位置完全连接的前馈网络(Feed Forward)。在两个子层的周围分别采用残差连接(Add),然后再进行层正则化(Norm)。每个子层的输出是LayerNorm(X+Sublayer(X)),其中Sublayer(X)是由子层本身实现的函数。为了促进这些残差连接,模型中所有子层以及嵌入层都产生维度为d_{model}=512的输出。
- 解码器:解码器也是由N=6个相同层堆栈组成,除了每个解码器层中的两个子层之外,解码器还插入了第三个子层Masked Multi-Head Attention,该子层对编码堆栈的输出执行多头注意。与编码器类似,在每个子层周围采用残差连接然后正则化。与编码器不同的是,这里增加了Masked Multi-Head Attention修改于Multi-Head Attention,防止当前的输入元素关注到后续的位置元素,这种掩码加上输出嵌入偏移一个位置,确保位置i的预测只能依赖小于i的位置的已知输出。
流程
下面以一个中文句子翻译为英文为例,简要说明步骤。
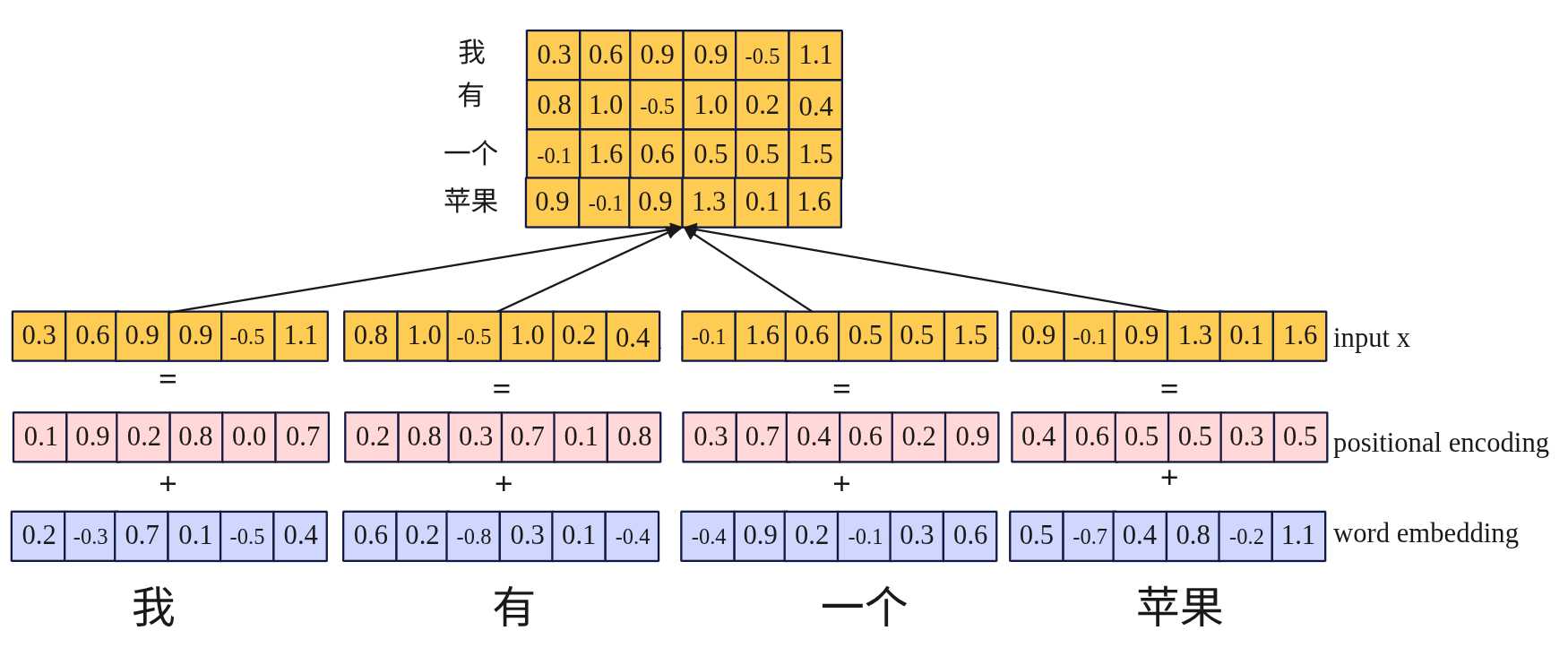
- word embedding: 输入的句子分词得到[“我”, “有”, “一个”, “苹果”],然后将每个词进行词嵌入(算法这里不阐述)转换为6维的向量。
- positional encoding:每个词进行位置编码,生成相关的位置信息。每个词的向量维度与词embedding维度一致。
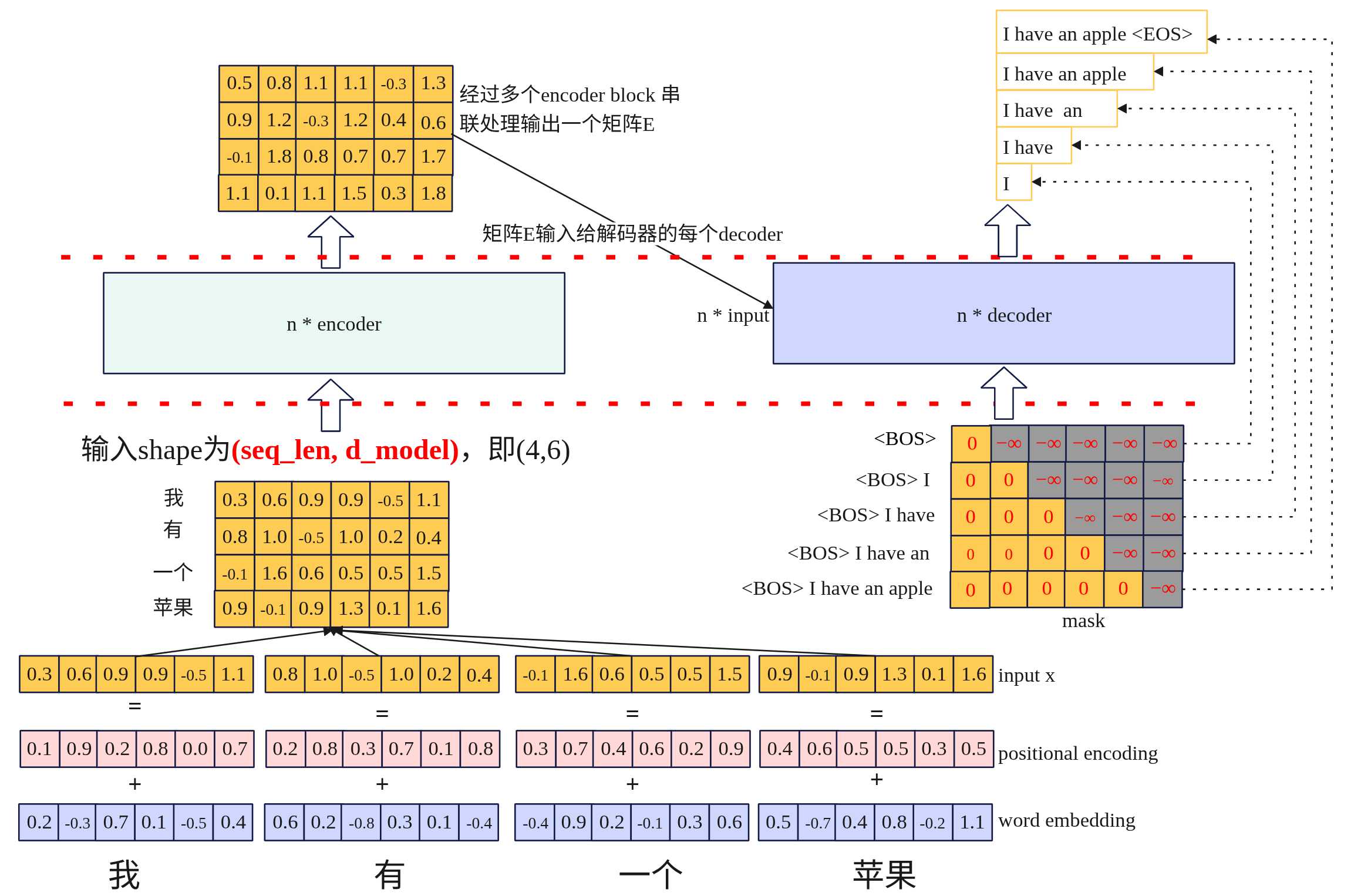
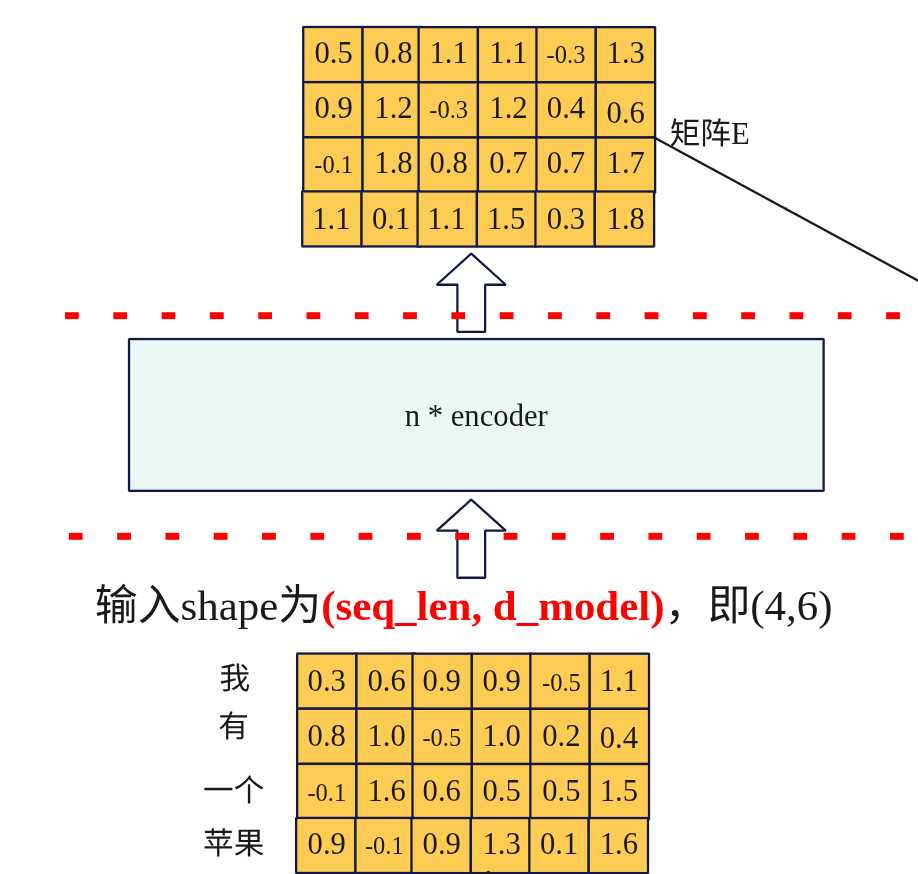
- transformer输入X: X=embedding + positional embedding,shape形状为(seq_len,d_model),其中seq_len为输入token数量,这里为4,d_model为词embedding向量维度。
- 编码输出矩阵E:输入X经过编码器后,经过自注意力分数等计算最后输出矩阵E将作为解码器的输入。矩阵E与输入的X形状一致。
- 解码输出:解码器的输出根据输入一个一个产生的,最开始的时候输入”BOS”代表开始将输出”I”,输入”BOS I”输出I have,输入”BOS I have”输出”I have an”…….。
- mask:在解码器内部有一个mask,其主要的作用是让生成步骤仅以来历史信息,不能访问未来的词。因为decoder是一个一个词生成的,自注意力层天然会计算序列中所有位置间的关联,若不施加约束,模型可能尝试为当前未生成的空白位置分配权重,生成第3个词时,模型默认会为第4、5等未来位置计算注意力权重(尽管这些位置尚无实际内容)。
输入
transformer的输入是一个多阶段的过程,核心的目标是将原始序列的数据转换为包含语义和位置信息的向量表示,这里重点分为word embedding和positional encoding。
word embedding
在进行word embedding之前,需要先把输入句子进行分词,得到离散的序列。如”我有一个苹果” → [“我”, “有”, “一个”, “苹果”]。
所谓word embedding词嵌入,就是将句子拆分的每个词映射到固定维度的向量,transformer论文中默认的向量维度为512,本文的示例是6维。如下:
- 我:[0.2, -0.3, 0.7, 0.1, -0.5, 0.4]
- 有:[0.6, 0.2, -0.8, 0.3, 0.1, -0.4]
- 一个:[-0.4, 0.9, 0.2, -0.1, 0.3, 0.6]
- 苹果:[0.5, -0.7, 0.4, 0.8, -0.2, 1.1]
关于转换映射的有很多方式,如随机初始化+训练学习的方式,或者word2vec,Glove等外部嵌入算法,这里就先不研究了。
positional encoding
自注意力机制本身不具备序列顺序的感知能力,而自然语言的语义高度以来次序,比如”猫爪老鼠”和”老鼠抓猫”含义就完全相反。因此需要显性的为每个词助于顺序信息,通过给每个位置进行编号,让模型感知词序。 而在transformer中,使用是的正弦函数和余弦函数给每个词生成唯一向量,其中偶数的向量维度使用正弦函数计算得到,基数使用余弦函数计算得到。其公式如下:
\begin{aligned} PE_{(pos, 2i)} &= \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) \
\ PE_{(pos, 2i+1)} &= \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) \end{aligned}
变量说明
- $pos$:词在序列中的位置(从0或1开始,示例中为1~4,如”我”是1,”有”是2,“一个”是3,”苹果”是4)
- $i$:向量维度索引(从0开始,文档示例中$d_{\text{model}}=6$,故$i=0,1,2$)
- $d_{\text{model}}$:模型隐藏层维度,也是word embedding向量维度(示例中为6,原始论文中为512)
下面基于d_mode=6说明计算过程,以第一个词”我”为例,计算其过程。
已知条件
- $pos=1$(第1个词的位置)
- $d_{\text{model}}=6$(向量维度为6)
- $i=0,1,2$(对应3对奇偶维度)
维度0(偶数位,2i=0):PE_{(1,0)} = \sin\left(\frac{1}{10000^{2×0/6}}\right) \approx 0.8 \quad
维度1(奇数位,2i+1=1):PE_{(1,1)} = \cos\left(\frac{1}{10000^{2×0/6}}\right) \approx 0.5 \quad
维度2(偶数位,2i=2):PE_{(1,2)} = \sin\left(\frac{1}{10000^{2×1/6}}\right) \approx 0.1 \quad
维度3(奇数位,2i+1=3):PE_{(1,3)} = \cos\left(\frac{1}{10000^{2×1/6}}\right) \approx 1.0 \quad
维度4(偶数位,2i=4):PE_{(1,4)} = \sin\left(\frac{1}{10000^{2×2/6}}\right) = \approx 0.0 \quad
维度5(奇数位,2i+1=5):PE_{(1,5)} = \cos\left(\frac{1}{10000^{2×2/6}}\right) \quad 1.0
最后得到”我”的positional encoding为[0.8,0.5,0.1,1.0.0.0,1.0]。
使用正弦函数、余弦函数进行编码有以下好处。
- 相对位置可学习:对于任意位置偏移k,PE_{pos+k}可表示为PE_{pos}的线性组合(利用三角函数的和角公式),使模型能轻松学习相对位置关系。
-
无界序列适应:公式基于指数函数衰减,对任意长度的序列(远超训练时的最大长度)均能生成有效编码,避免了学习型位置编码的泛化性问题。
-
数值稳定性:正弦/余弦函数的值域固定在[-1,1],与词嵌入向量相加后不会导致数值范围剧烈波动,有利于模型训练稳定。
注意力机制
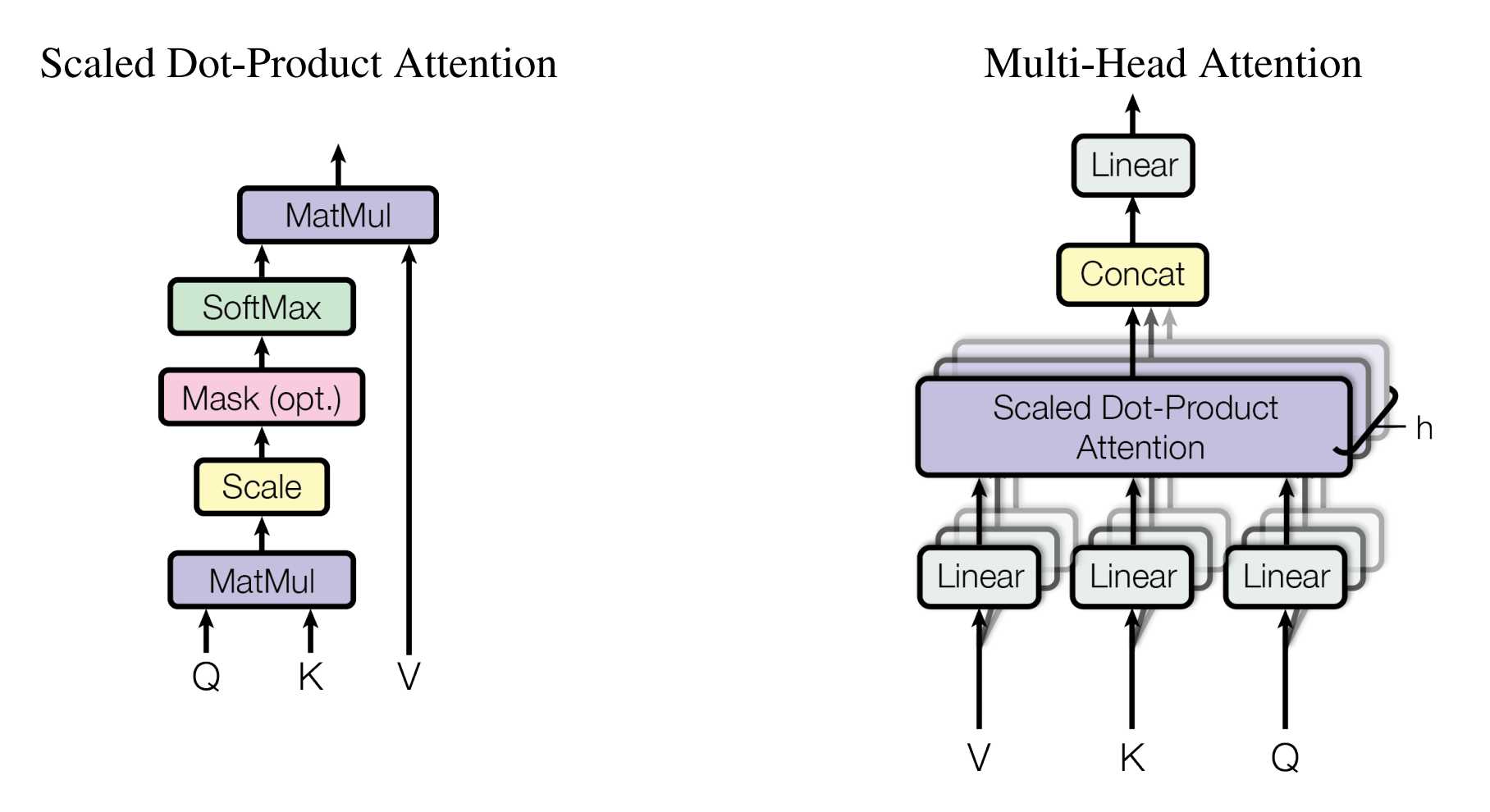
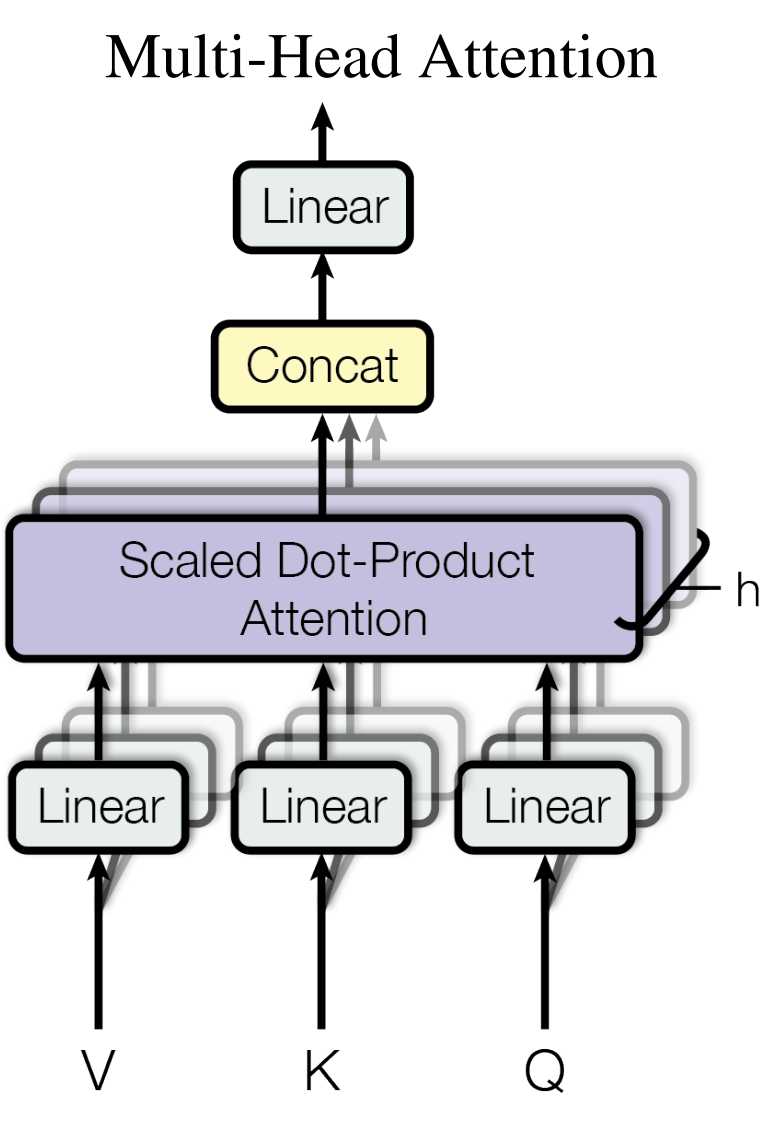
在transformer中最关键的就是Multi-Head Attention,本小节先来重点分析其实现原理。Multi-Head Attention由多个Scaled Dot-Product Attention组成。
注意力函数可以描述为将查询(Query)和一组键值对(Key-Value)映射到输出,其中查询、键、值和输出都是向量,输出计算为加权和。
Scaled Dot-Product Attetion
其核心的公式就是如下:
\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V
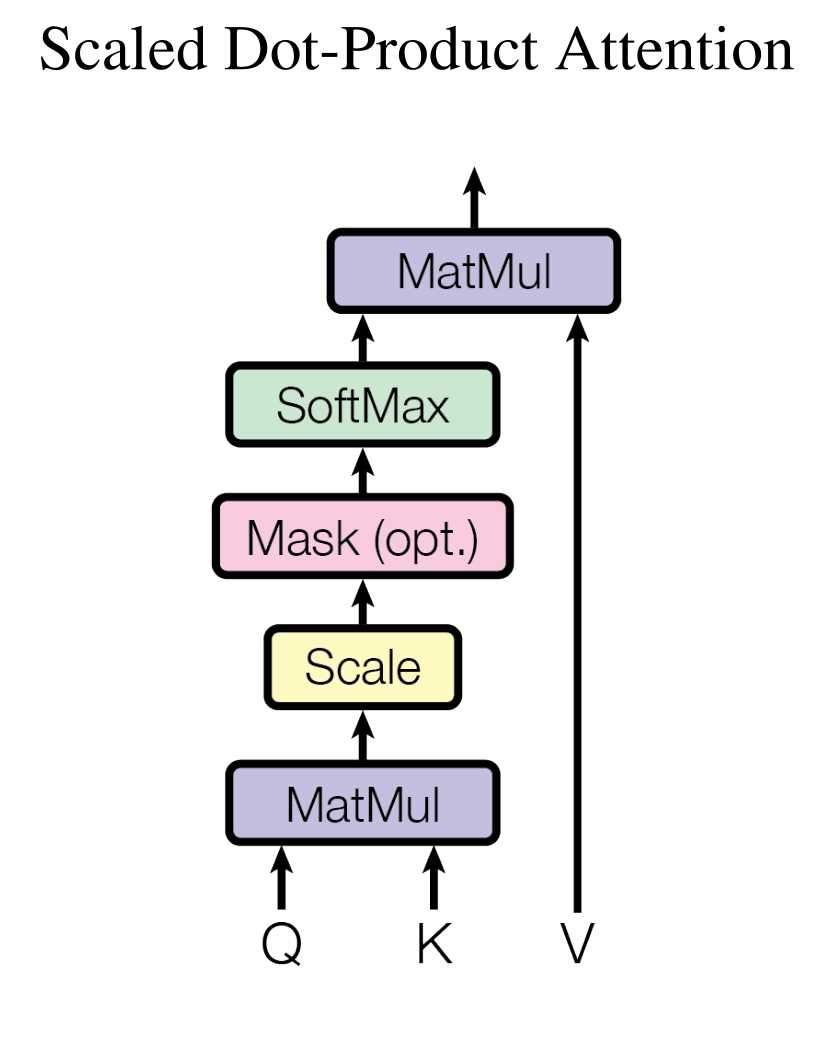
对于Scaled Dot-Product Attention自下而上计算的流程如下:
- MatMul:输入查询矩阵 Q(目标序列)与键矩阵 K(源序列)进行矩阵乘法,主要用于计算原始相关性的分数。\text{Scores} = QK^T
- Scale:缩放的目的是防止计算的分数导致softmax梯度消失,因此对结果进行缩放。\text{Scaled Scores} = \frac{\text{Scores}}{\sqrt{d_k}}。
- Optional Mask:mask用于遮挡无效位置(如未来词或填充符),训练是设置-inf,只有在解码器的时候用。
- SoftMax:对计算分数进行归一化,输出注意力权重权重概率分布。\text{Weights} = \text{softmax}(\text{Masked Scores})
- MatMul:前面的QK计算得出了目标词在句子中的哪些词相关性比较大,也就是得到一个注意力分数,最后根据注意力分数做加权求和到最后的目标词上下文信息向量。\text{Output} = \text{Weights} \cdot V
接下来我们展开按照流程来分析一下。
计算QKV
Transformer中引入Q(Query)、K(Key)、V(Value)三元组的设计是注意力机制的核心创新,使用QKV本质是实现动态语义的聚集。传统的传统RNN/CNN在长距离建模时存在固有缺陷,CNN依赖局部卷积核,RNN受制于顺序编码,无法动态关注全局关键信息。而使用QKV三元组模拟”信息检索系统”
- Query(查询):表示当前需要关注的内容,需要“寻找什么信息”(如翻译中”apple”要找出”苹果”的语义需求)。
- Key(键):描述源信息的特征标签(如中文词”苹果”的语义属性)。
- Value(值):存储实际待提取的信息本体(如”苹果”的词嵌入向量)。
自注意力机制就是用q去找相关的k,得到注意力分数,然后通过注意力分数去从v中提取信息。
如翻译“I have an apple”时,生成“apple”的Query会去找跟(“苹果”)相关的key计算高相似度,然后用得到的K取提取Value(“苹果”的语义向量),实现精准跨语言对齐。
使用Q MatMul K的方式可以量化查询的需求与源特征的匹配程度,最后在MatMul上V是因为做最终的提取。
既然Q MatMul K是量化查询需求与源特征的匹配程度,那么每个词一般都是在句子中去理解的,所以每个词都需要去计算在句子中其他词的关联。
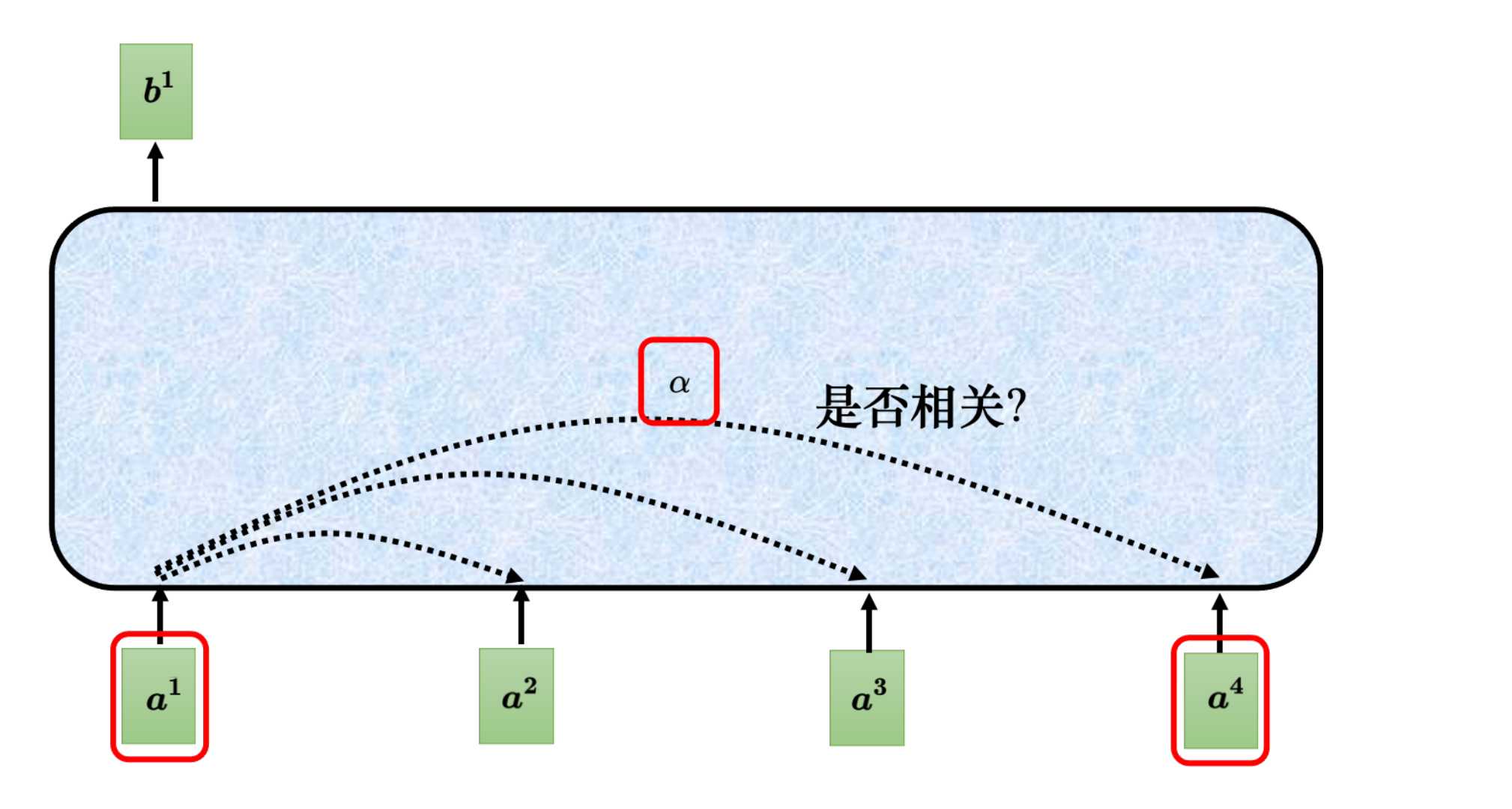
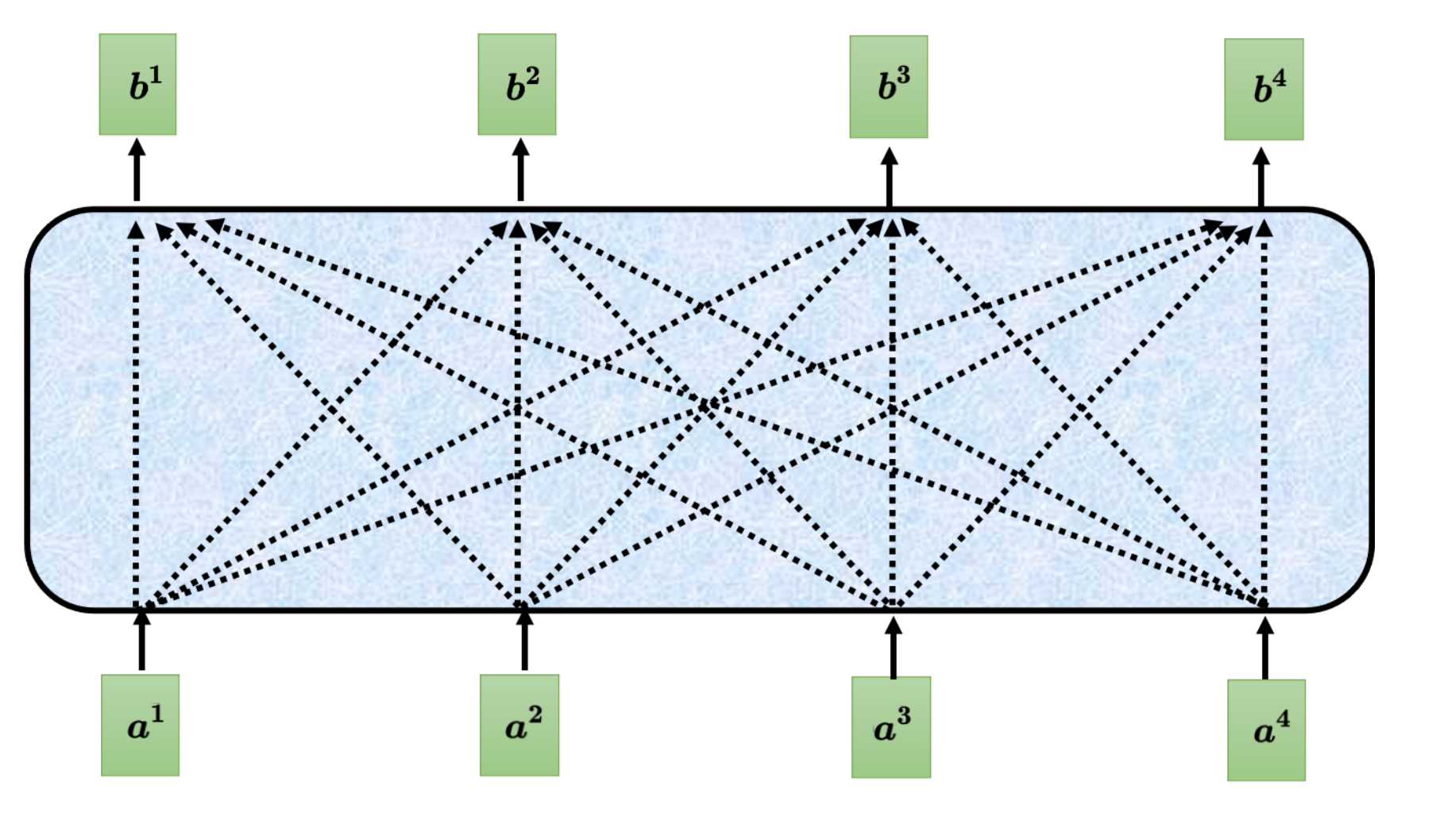
每个都需要与句子中的其他进行相关性计算,各自得到一个输出。如a1最终计算出得到b1,a2计算得到b2……。
(1)以单个词为例说明运作流程
下面以a1为例:
- 首先a1先自己计算出q1,q1=Wq a1,其中Wq为权重参数。
- 其次句子中所有词a1,a2,a3,a4分别乘Wk计算各自得到k1,k2,k3,k4。
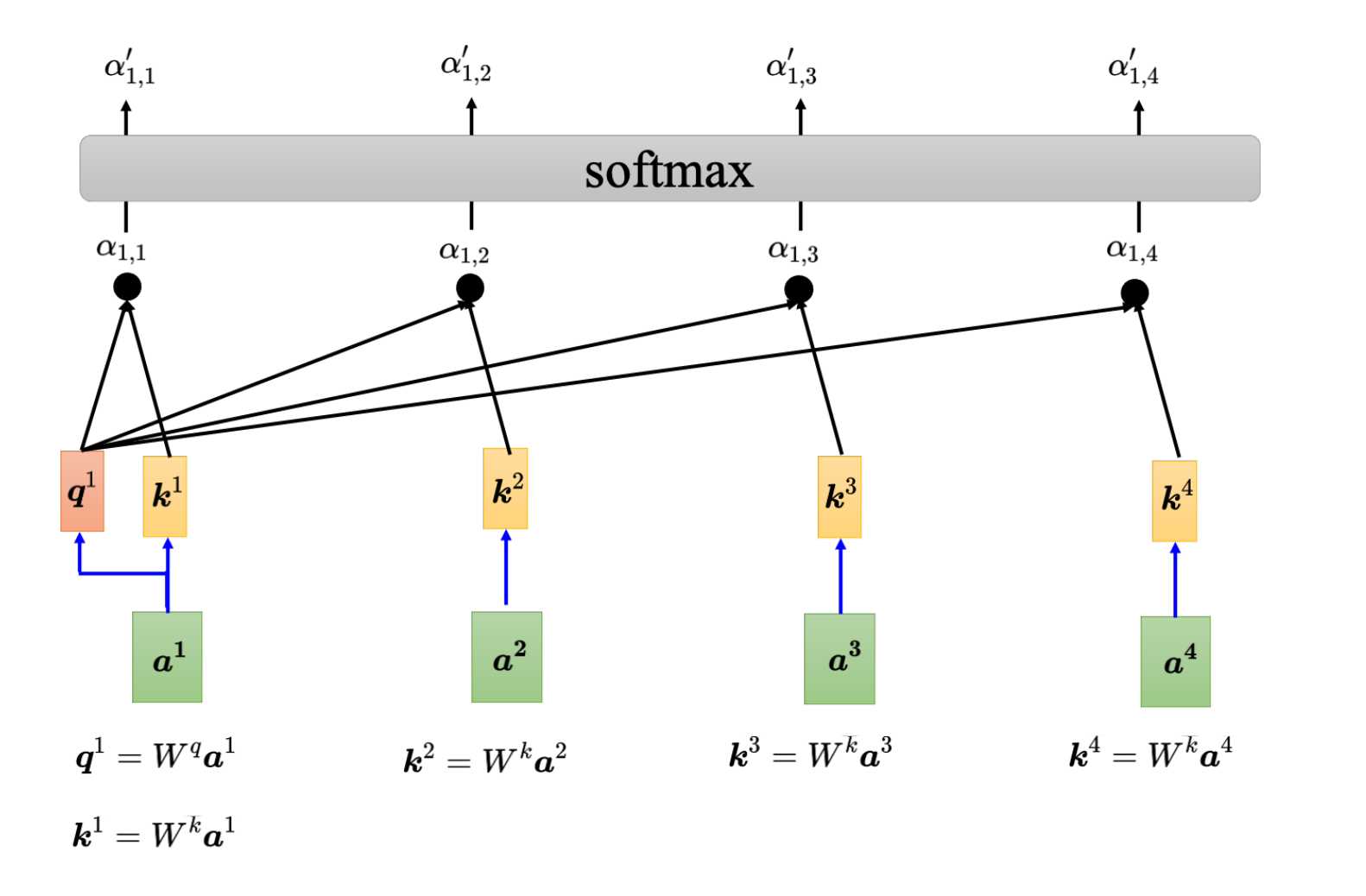
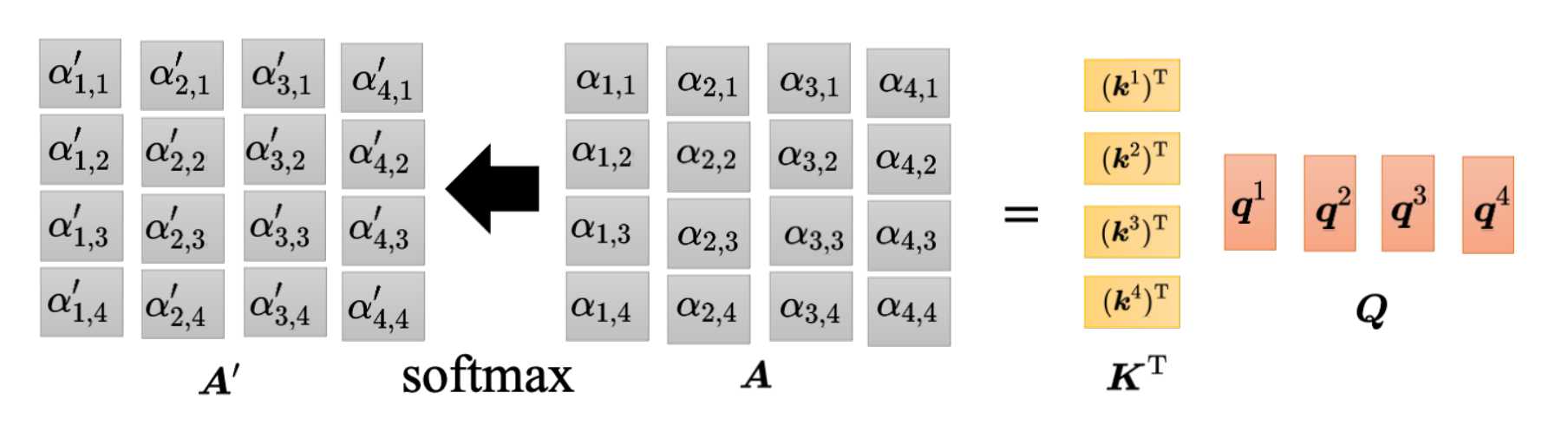
- 接着q1分别与k1,k2,k3,k4分别做点积计算得到a11,a12,a13,a14。
- 最后在对a11,a12,a13,a14做softmax得到最终的结果。a’11,a’12,a’13,a’14。
为什么要做softmax了?
- 归一化概率:将原始分数(可能为任意实数)转换为概率分布,使得所有权重和为1,便于后续的加权求和操作(即用这些权重来加权值向量)。
- 增强区分度:softmax 的指数运算会放大高分数的影响,同时抑制低分数。这样,模型可以更加关注最相关的键,而忽略不相关的键。在图中,如果某个 α{1,i} 较大,经过 softmax 后其对应的 α'{1,i} 会远大于其他较小的分数对应的权重,从而实现选择性聚焦。
在对softmax之前还要进行一次scale这里就不周赘述了。
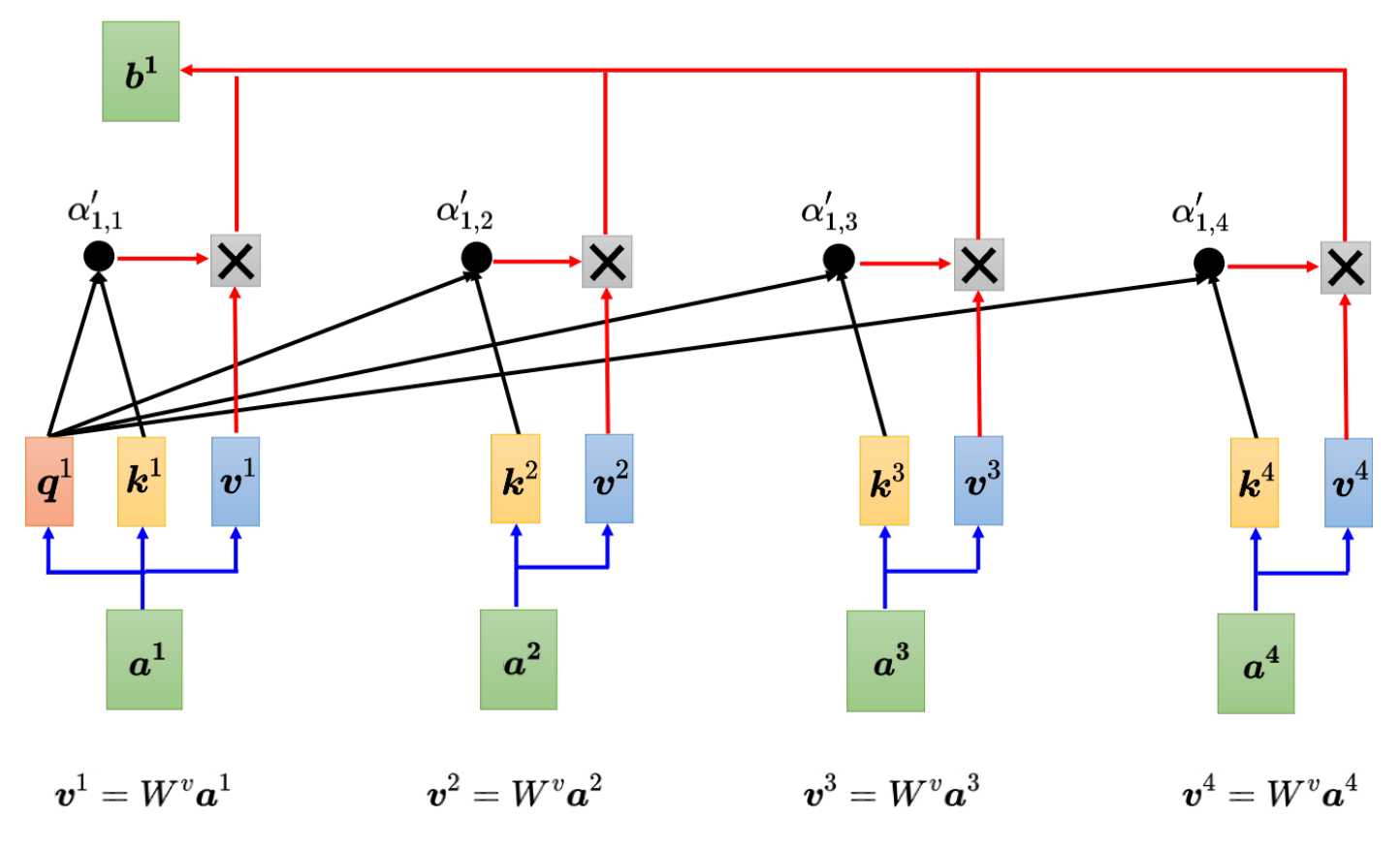
a’11,a’12,a’13,a’14即为a1对句子中每个词的注意力分数,计算出值后就可以根据其值从序列里面抽取出了重要的信息,根据a’11,a’12,a’13,a’14可知输入的词向量哪些跟与a1相关性大,接下来即可根据关联性(即注意力分数)抽取重要的信息。
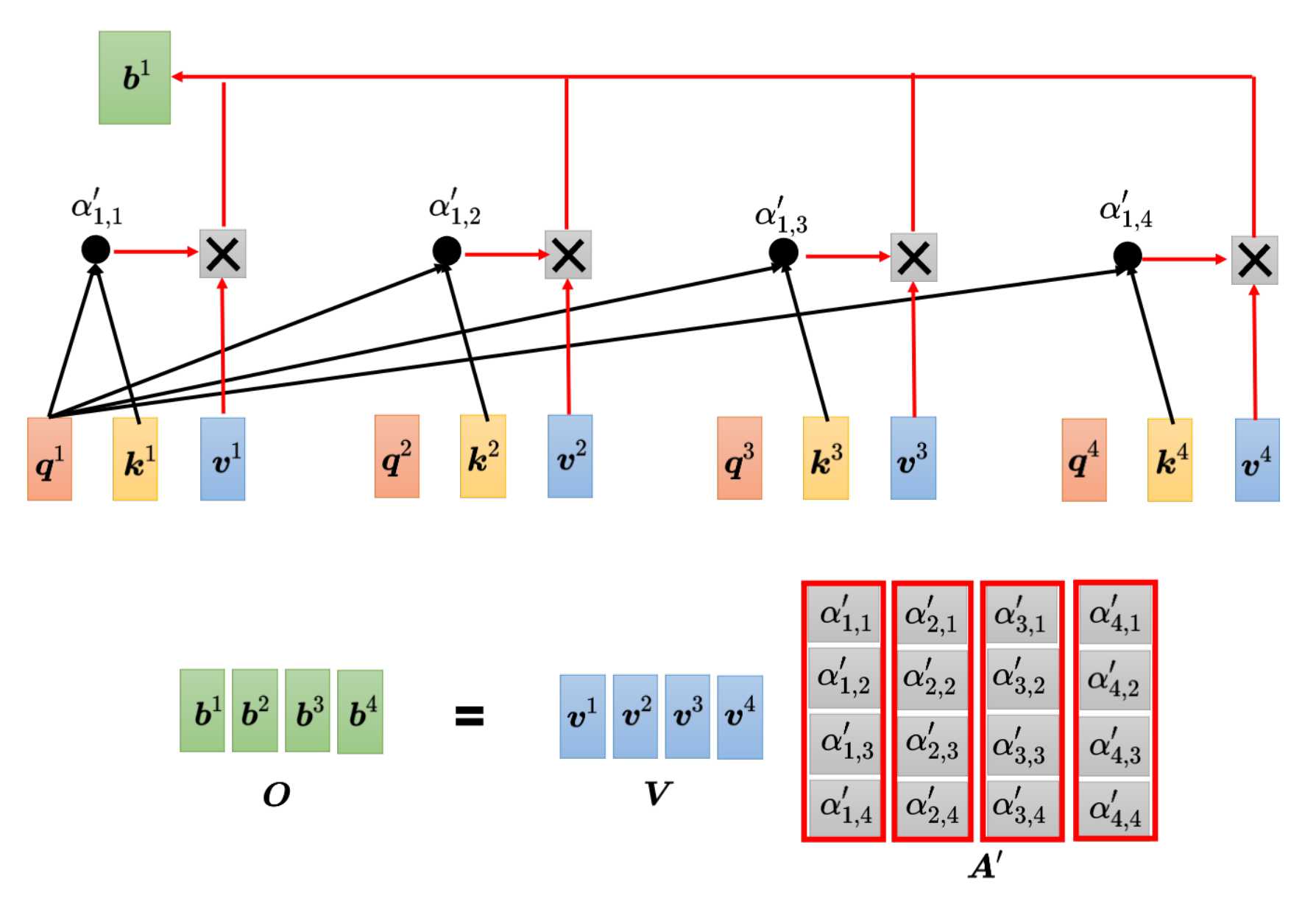
将向量a1~a4分别乘以Wv权重得到新的向量v1,v2,v3,v4,将其中的每一个向量分别乘以注意力分数a’xx,再把结果加起来。
b_1 = \sum_{i} \alpha’_{1,i} v_i
如果a1和a2关联性强,即a’12的值就很大,那么在做加权和以后,得到的b1就越接近与v2,所以谁的注意力分数越大,谁的v就会主导抽取结果。同理可以计算出b2,b3,b4。
(2)以矩阵乘法角度说明运作流程
上面的过程是单个词的计算过程,但是实际在自注意力模型的运作过程中,是通过矩阵乘法的方式计算的,这样效率才高,接下来看看从矩阵乘法的角度理解运行过程。
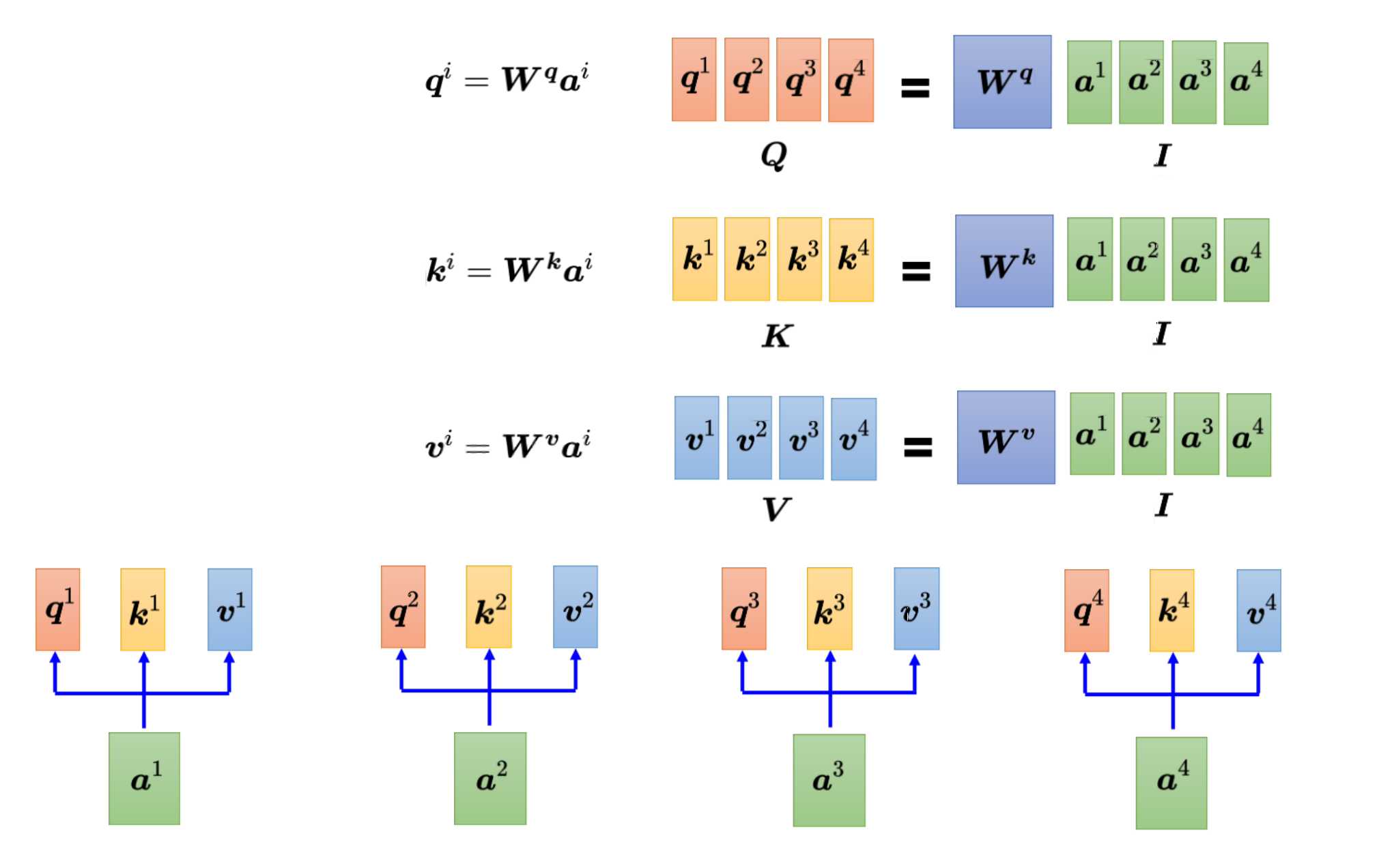
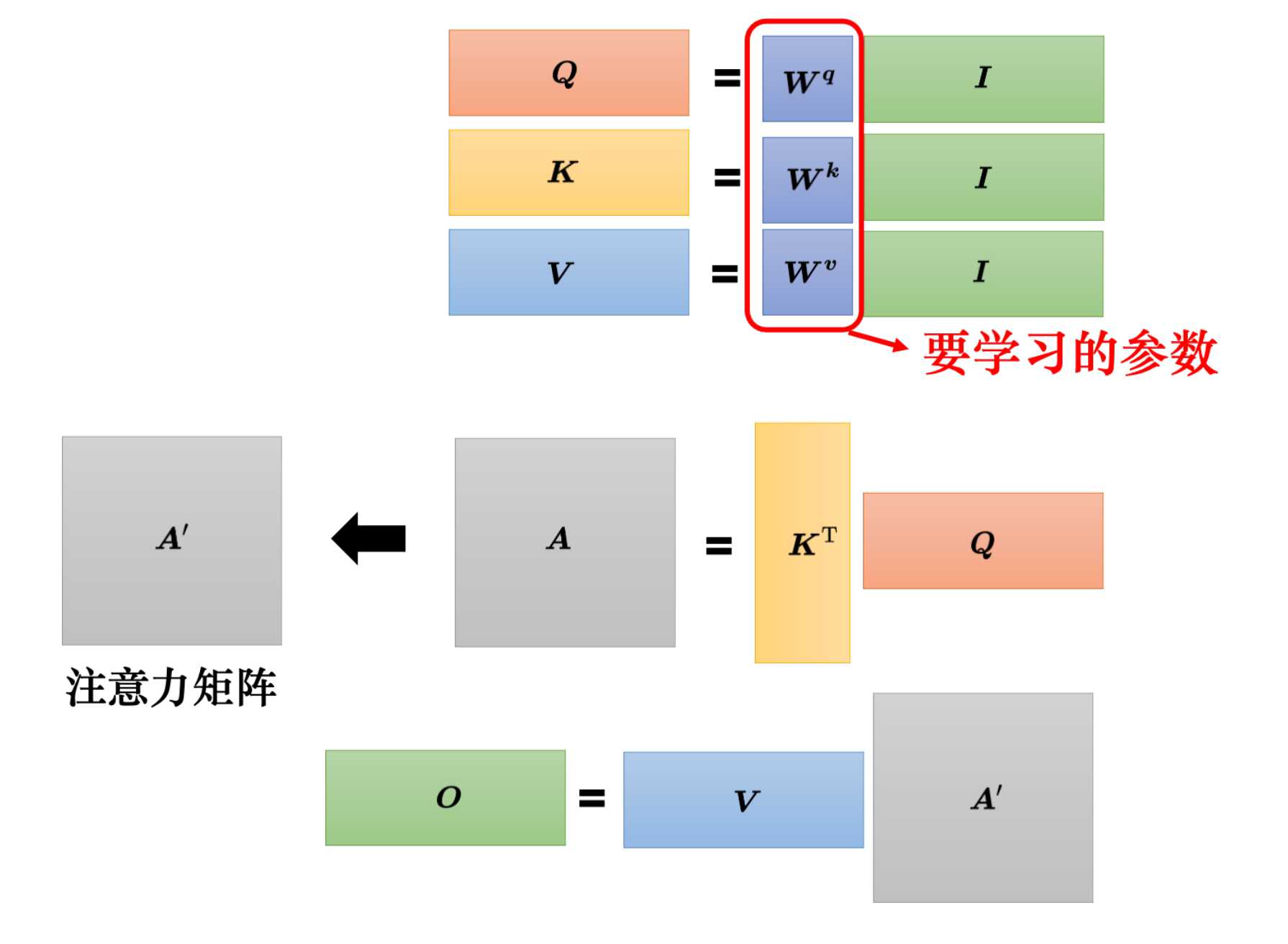
因为每个词都要产生qkv,即每个ai都要乘以权重参数Wq得到qi,那么可以把这些ai合并起来当做一个矩阵,即把a1到a4拼接起来,看成一个矩阵I,矩阵I有4列,其中每一列都是自注意力模型的输入。把矩阵I乘以矩阵Wq,就可以得到Q。其中Wq则是权重参数,Q则可以看成q1~q4的拼接。
同理产生k和v的操作跟q一模一样,计算得到K,V矩阵。
通过两个Q与K转置相乘就可以得到注意力分数的矩阵A,然后将A经过softmax得到A’。
最后使用注意力分数A’提出V,得到最终的输出矩阵O,即b1~b4的拼接。
最后总结下,自注意力模型输入是一组向量,将这些向量拼接起来得到I,让后将I分别乘以三个矩阵Wq,Wk,Wq,得到另外三个矩阵QKV,将Q乘以K的转置得到A,然后对A在做一些处理得到A’,A’为注意力分数矩阵,将A’乘以V提取出特征,最后得到自注意力的输出O。
Multi-Head Attention
论文中阐述,与其使用一套维度为d_{model}的单头注意力,还不如把输入的Query、Key、Value各自用不同的、可学习的线性投影经过注意力机制映射出h份版本,每份的维度更小,计为d_{k}和d_{v}。
在每一份(也就是每个头)上各自并行计算注意力,得到d_{v}-维的输出,然后再把所有头的输出沿特征维度拼接,再做一次线性投影到得到最终的输出。
为什么要做多头?多头可以“同时在不同表示子空间里看信息”。一个头往往只能聚焦一种关系(比如短距依赖),多个头能并行关注不同关系(长距、句法、语义等)。如果只有单头,容易把多种关系“平均混在一起”,表达力受限。
多头注意力会把输入进行降维值C/h,这样每个头的输入维度就为C/h。为什么使用”多头+降维”而不是”多头不降维”,主要会是考虑如果每个头都保持默认的输入C维,h个头拼接后会是[B, L, h·C],参数量与计算复杂度都膨胀 h 倍,不经济。标准做法让每头维度变为 C/h,拼接回到 C,因此总计算/参数量与单头同量级,但表达力更强(多视角、子空间解耦)。
下面是来说明一下多头注意力机制是如何计算的,下面省略了输入降维的过程。
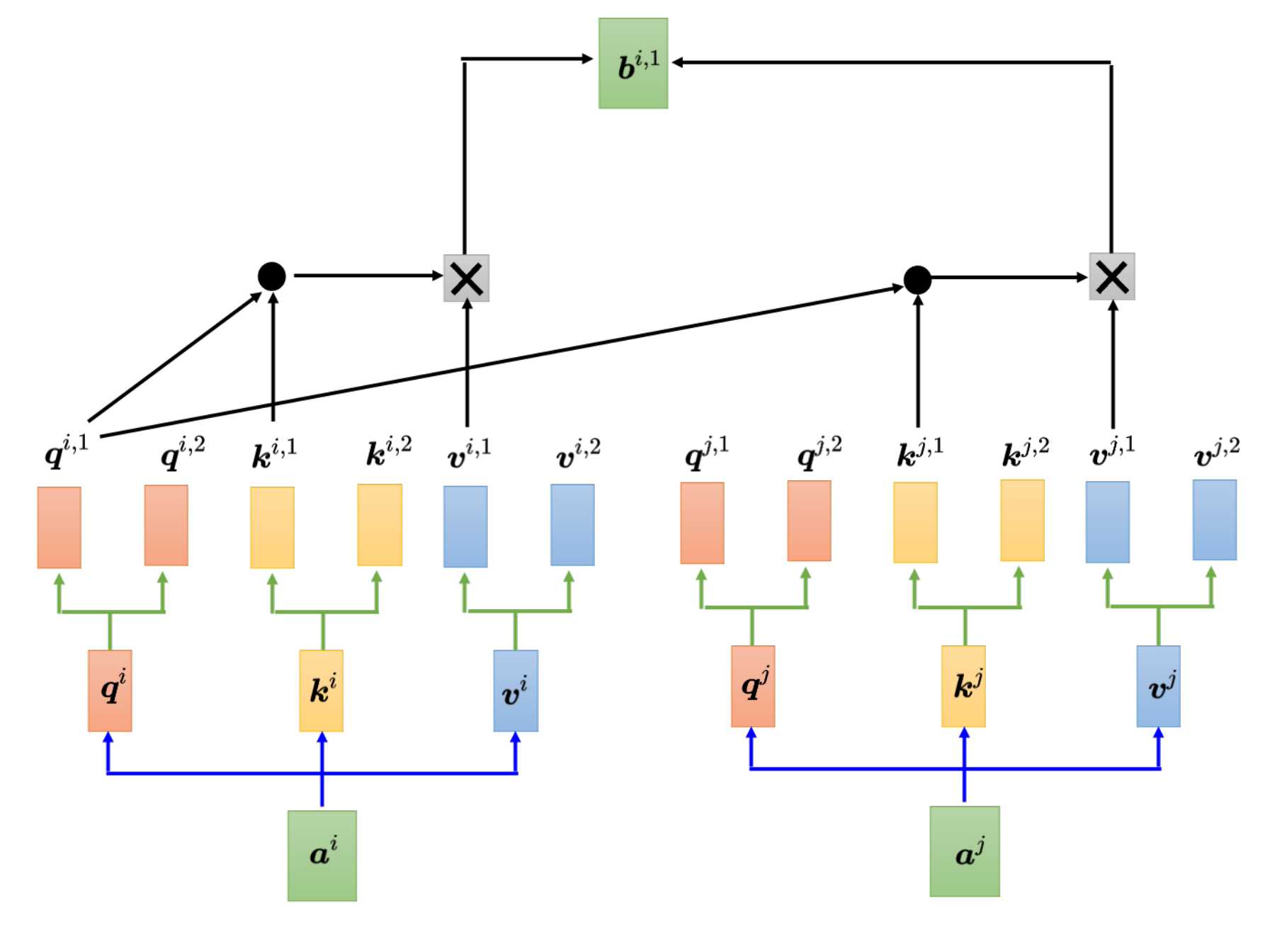
如上图,先把a乘以一个矩阵得到q,然后再把q乘以另外两个矩阵得到q1,q2。qi1和qi2代表的有两个头,表示要查询两种不同的相关性,那么既然有两个q,k,v也得需要两个,同理得到各自的两个k,v。
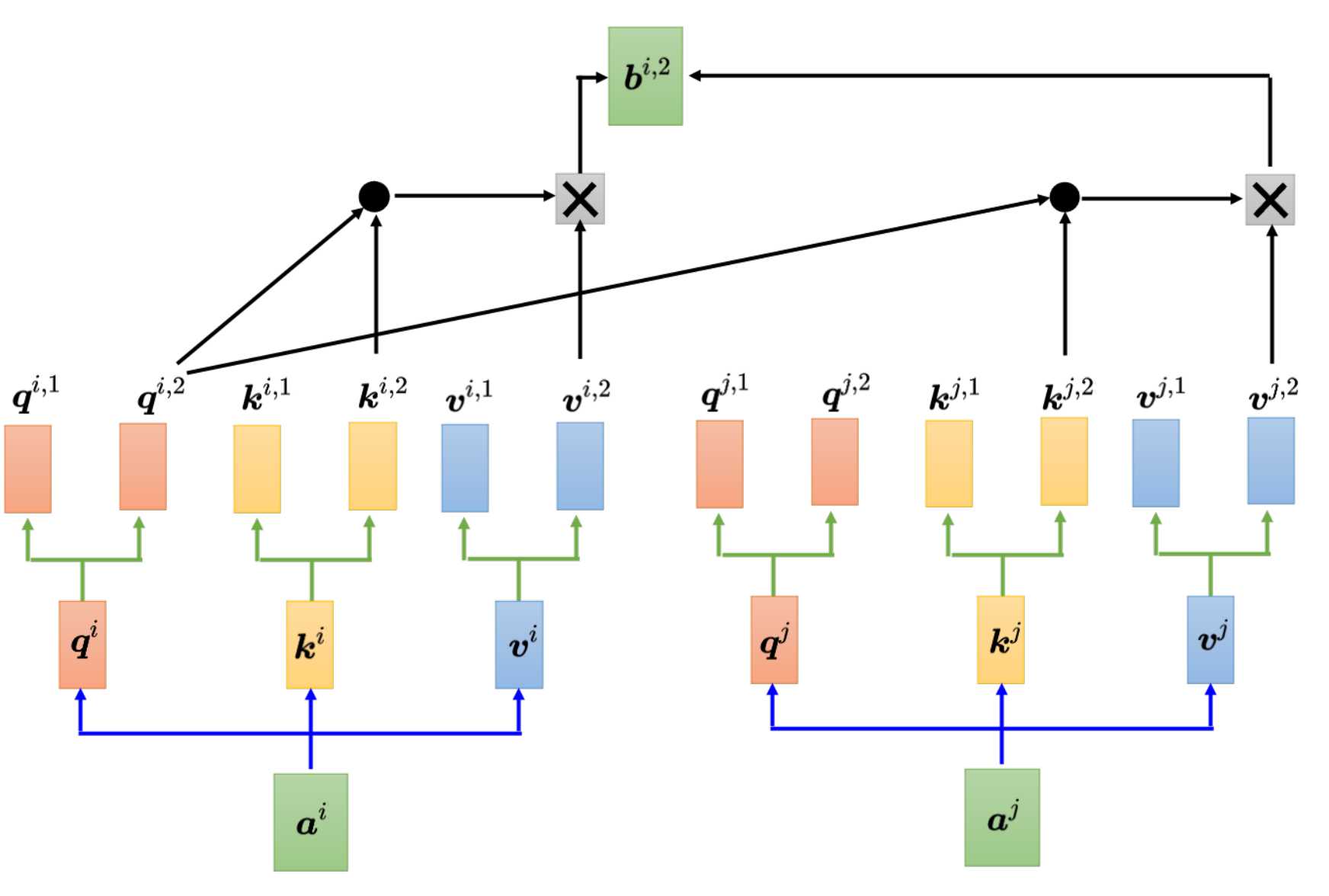
关于多头注意力机制的计算跟上一节的计算类似,各自的头计算各自的,如上图是计算头1,下图是计算头2。
通过各自头的计算,那么将会得到各自头的一个输出bi1,bi2,最后需要将bi1和bi2拼起来,先乘以一个矩阵进行变换得到bi,再送到下下一层。
encoder
编码器有多个相同的子编码器叠加而成,最小单元的子编码器由Multil-Head Aattention、Add & Norm、Feed Forward这几个组件构成,Multil-head Attention前面已经解释了,接下来重点分析剩余模块的流程。为表述方便后面的编码器都默认指最小单元的编码器。
Add & Norm
Add & Norm在编码器一个block中出现了两次,首次出现是位于 Multi-Head Attention(橙色模块)的输出端,再次出现是位于 Feed Forward(蓝色模块)的输出端。如下图:
(1)残差连接
残差连接的作用是在深层网络中,梯度在反向传播时可能会消失或爆炸。残差连接通过将输入直接加到函数输出上(即 F(x) + x),提供了一个恒等映射的路径。这使得梯度在反向传播时可以直接流过,从而缓解了梯度消失的问题,使深层网络训练成为可能。
Add操作是残差连接(Resudual Connection),其公式
\mathbf{y} = \mathcal{F}(\mathbf{x}, {\mathbf{W}_i}) + \mathbf{x}
(2)层归一化
层归一化的作用是在残差连接之后,数据的分布可能会发生变化,可能会导致后续层的学习变得困难,使用层归一化能够重新调整数据分布(如将每一层的输出归一化为均值为0,方差为1),从而加速训练并提高模型的泛化能力。
层归一化计算公式步骤如下:
这里使用的是层归一化而非批归一化,主要是可以独立处理每个样本,应对变长序列输入,同时对小批量训练不依赖批量统计量。
为什么Add&Norm要成对使用?
每个主要计算层后面都有Add & Norm,形成了一种模式:计算层 -> Add & Norm。这样,每个计算层的输出在传递给下一层之前都会被重新调整,使得模型在训练过程中保持稳定。如果只有残差连接而没有归一化,那么随着层数的增加,输出的尺度可能会不断增长,导致训练不稳定;如果只有归一化而没有残差连接,则可能无法解决深层网络中的梯度消失问题。
Feed Forward
先来看看什么是Feed Forward,前馈神经有两层全连接神经网络组成,中间使用非线性激活函数(通常是ReLU),数学表达式如下:
FFN(x) = \text{ReLU}(xW_1 + b_1)W_2 + b_2
(1)特征扩展,将特征维度从512扩展至2048
\boxed{
h_i = \text{ReLU}(
\underbrace{x_i}_{1 \times 512} \underbrace{W_1}_{512 \times 2048} + b_1
)}
- $x_i$:位置$i$的输入向量($1 \times 512$)
- $W_1$:扩展层权重矩阵($512 \times 2048$)
前面输入attention结果本质上计算是加权平均,都是线性操作,这里引入ReLu非线性变化,使模型能学习更复杂的函数映射。同时升维可以在高维空间捕捉更细微模式。
(2)进行特征压缩,将特征从2048压缩回512
\boxed{
y_i = \underbrace{h_i}_{1 \times 2048}
\underbrace{W_2}_{2048 \times 512} +
b_2
}
- $h_i$:ReLU激活后的特征向量($1 \times 2048$)
- $W_2$:压缩层权重矩阵($2048 \times 512$)
最后再从高维进行降维,保持与后续模块的兼容性。
总结一下FFN的作用有如下:
- 高纬投影:将输入映射到高维空间(如512→2048),捕获更复杂的特征组合。
- 非线性激活:引入非线性(如ReLU),打破线性变换限制,增强模型表达能力。
- 低维还原:将特征压缩回原始维度,保持与后续模块兼容性。
encoder block
Multi-Head Attention、Add & Norm、Feed Ward构成了一个encoder block。
每个encoder block接入输入矩阵Xnd,并输出一个矩阵Ond,再把输出的O当做输入传递给下一个encoder,通过多个encoder的叠加,最后一个encoder block输出的就是编码信息矩阵E,用于送入到解码器中,就完成transformer的Encoder。
decoder
decoder与encoder大致的结构类似,但是也有差别主要由Masked Multi-head Attention、Multi-head Attention、Add & Norm、Feed Forward组成,这里唯一不一样的是Masked Multi-head Attention,接下来分模块介绍一下关键流程。
Masked Multi-head Attention
Masked Multi-head Attention通过一个掩码来阻止每个位置选择器后面的输入信息。
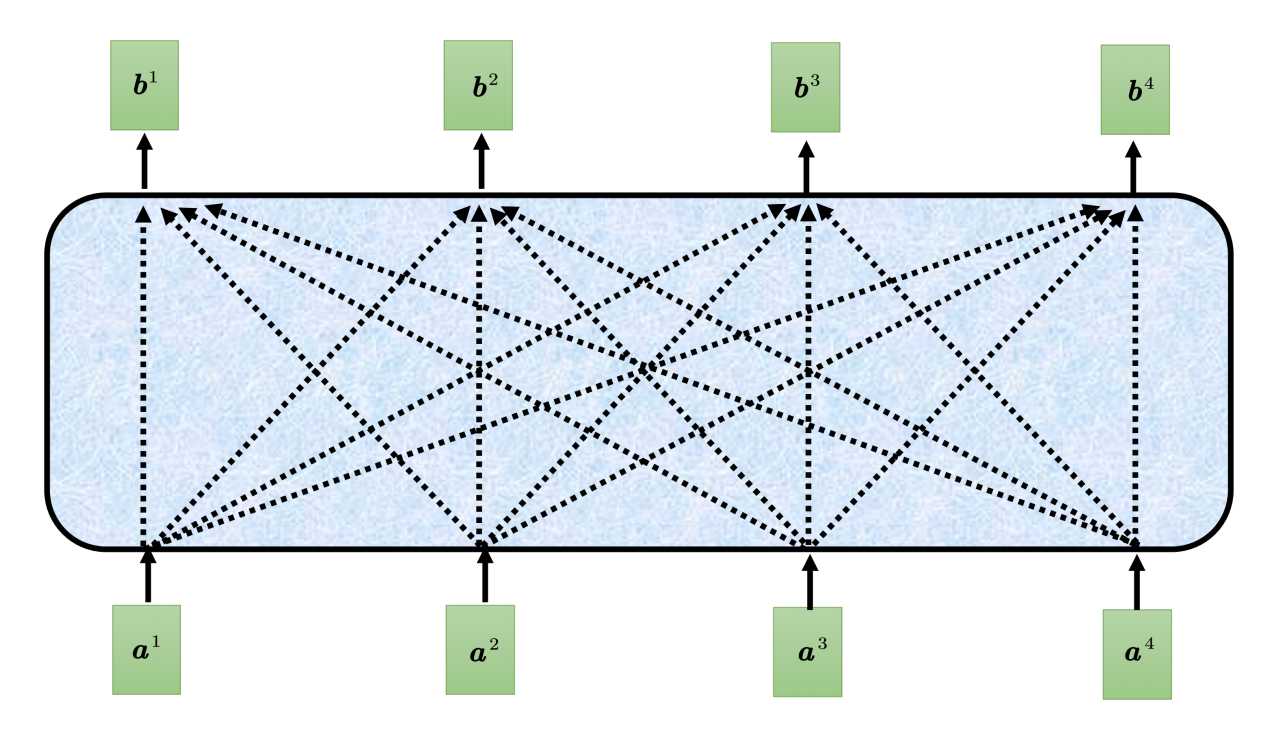
Multi-head Attention自注意力输入一排向量,自己输出另一排向量,这一排向量中的每个项链都要看过完整的输入后才能决定。如上图必现根据a1,a2,a3,a4的所有信息来输出b1。
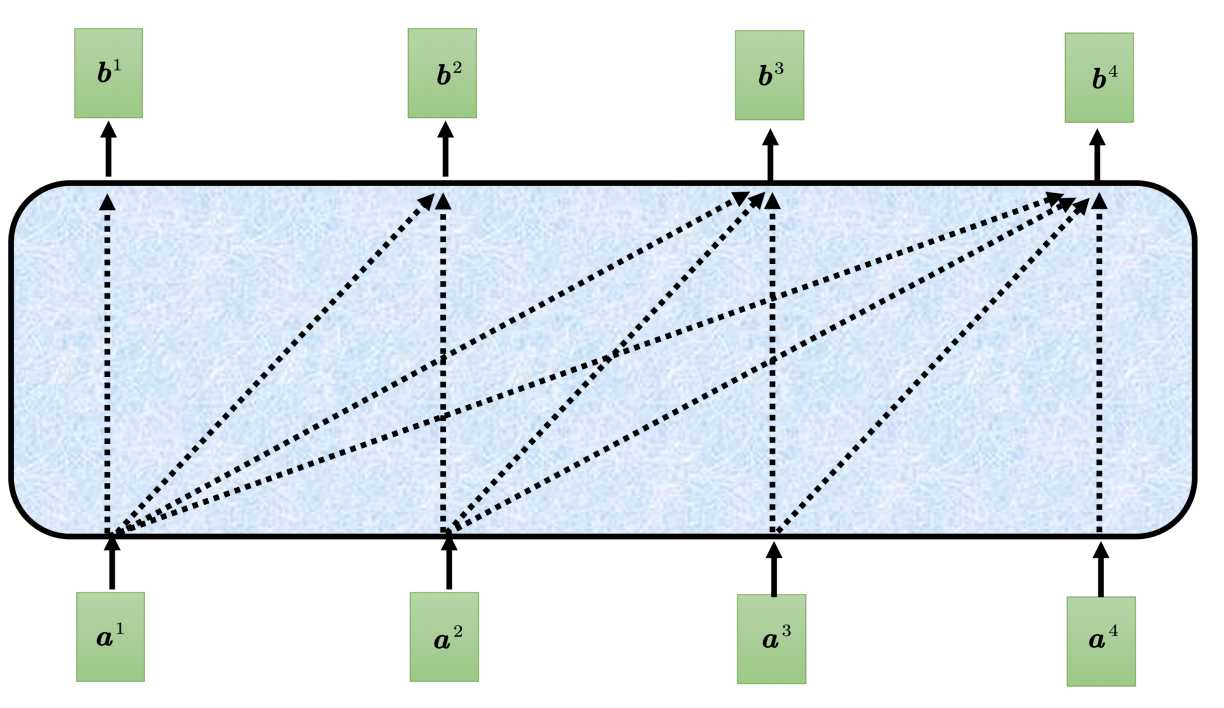
而掩码多头注意力则不再看右边的部分,如下图。
在产生b1的时候,只考虑a1的信息,不再考虑a2,a3,a4的信息。在产生b2的时候,只考虑a1,a2的信息,不再考虑a3,a4的信息,在产生b3的时候,只考虑a1,a2,a3的信息,不再考虑a4的信息,只有在阐述b4的时候,才考虑整个输入序列的信息。
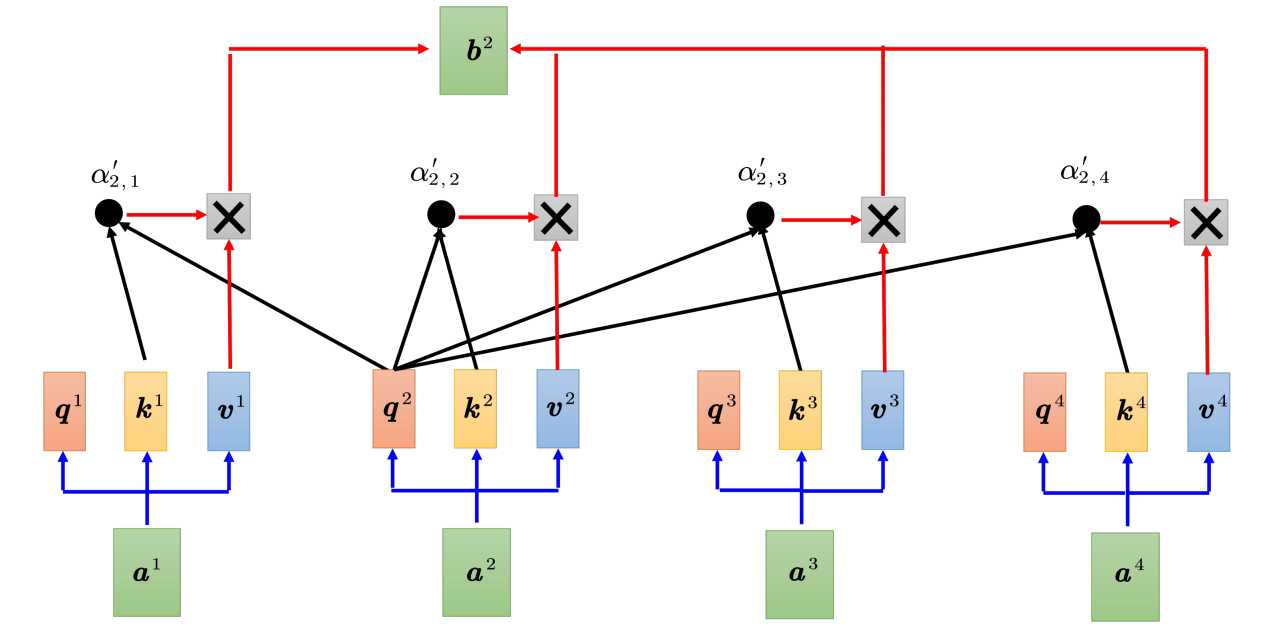
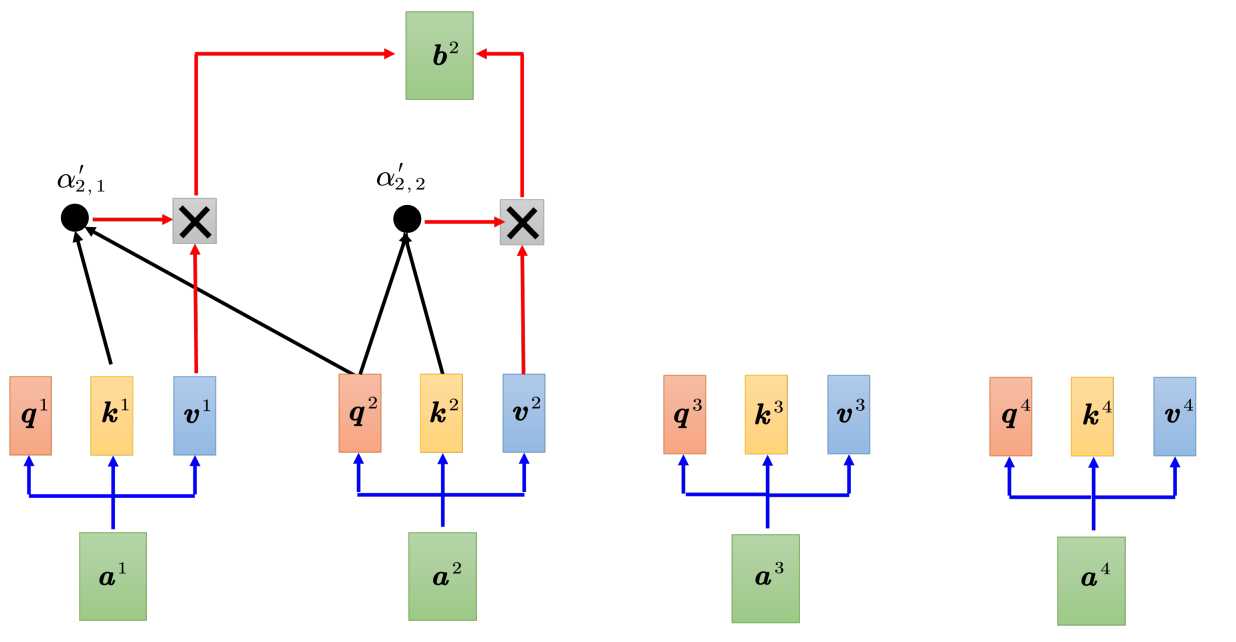
下面是Multi-head Attention产生b2的过程,b2需要和a1,a2,a2,a3的qkv信息计算得到b2。
而如果是Masked Multi-head Attention,b2只需要拿q2和k1、k2计算注意力,最后只计算v1和v2的加权和,不管a2右边的部分,则计算过下。
为什么在注意力机制中加上掩码了?
因为解码器的输出是一个一个产生的,只能考虑左边已经生成的部分,而没有办法考虑未生成的右边部分。举个例子,先有得a1,再有a2,接下来是a3,然后是a4。这个跟编码器中的self-attention不一样,编码器中的是a1,a2,a3,a4一次性输入模型,编码器一次性处理输出。正因为解码器这个特性,现有a1,才能预测输出a2,再有后面的a3,a4,所以当我们在计算b2时,a3,a4实际是还没输出的,所以没有办法考虑a3,a4。
Multi-head Attention
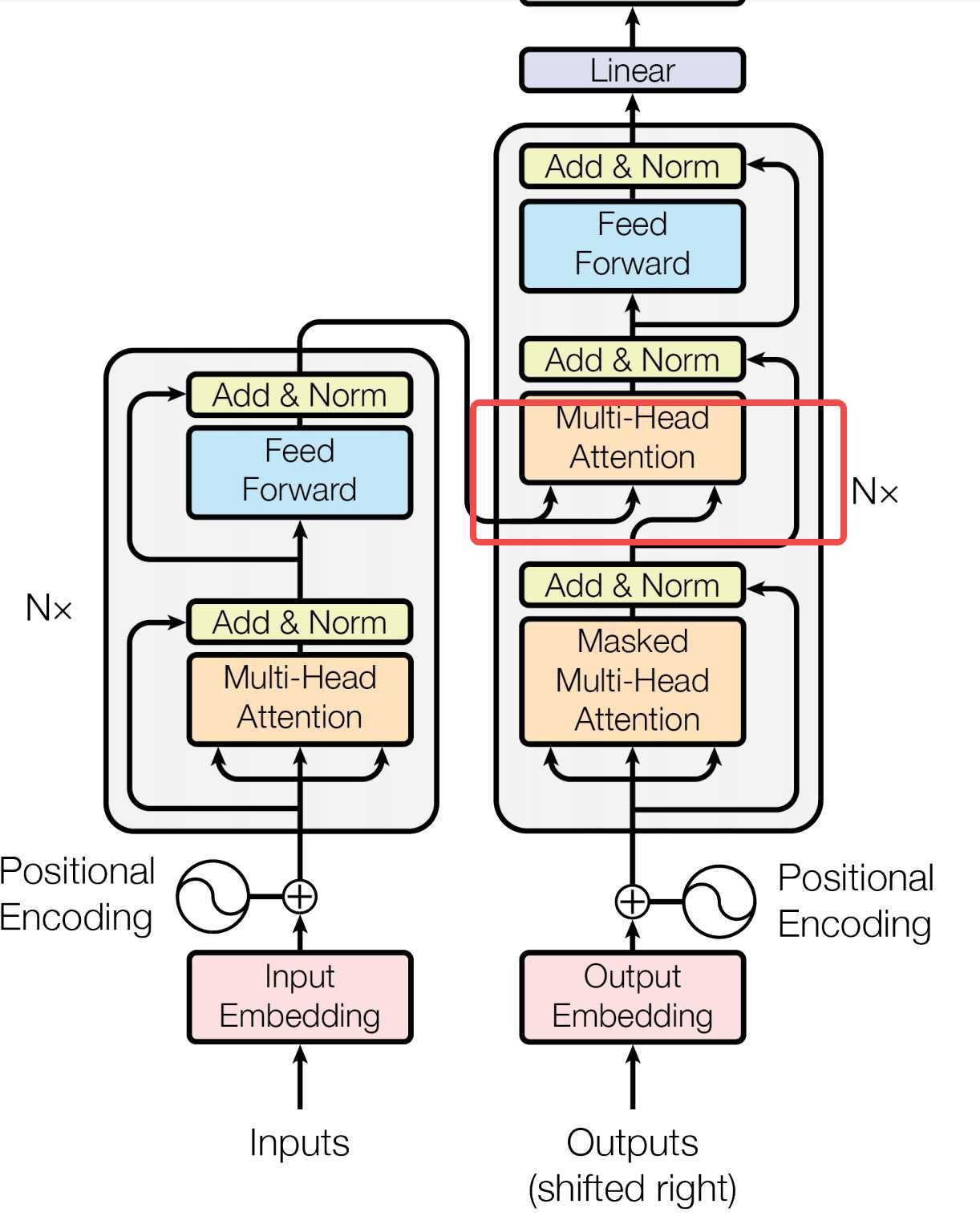
第二个Mult-head Attention也称为交叉注意力,结构组成与编码器没什么差别。主要的差异点计算输入,解码器的第二个Multi-head Attention(交叉注意力)输入,这个注意力层的Query来自解码器前一层(通常是解码器的第一个Masked Self-Attention层)的输出,而Key和Value则来自编码器的最终输出(即最后一个编码器层的输出)。因此,该注意力层的目的是让解码器在生成当前输出时能够关注到输入序列的相关部分。
输出
transformer最后的输出层是linear层和softmax层。
- linear层:将解码器输出的高维语义向量映射到词汇表空间,输入为(batch_size, seq_len, d_model),输出为(batch_size, seq_len, vocab_size),主要的作用是将抽象语义转换为具体词汇的匹配分数(Logits)。
- softmax层:将Logits转换为概率分布,输入为Logits矩阵,输出为(batch_size, seq_len, vocab_size)的概率张量,满足概率约束(和为1),支持损失计算与生成任务。
Linear层
Linear层主要作用是计算解码器向量与每个词嵌入的点积,得到词汇表中每个词的原始匹配分数,计算公式为。
Logits = X \cdot W^{T} + b
- X:解码器最后一层输出(形状 [batch_size, seq_len, d_model],例:[1, 4, 6])
- W:权重矩阵(形状 [vocab_size, d_model],例:50000×6)
- b:偏置项(可选)
最终的输出是词汇表中每个词的概率(形状 [batch_size, seq_len, vocab_size],例:[1, 5, 10000]),假设这里的词库为10000个。
如下:
logits = [
"I": 8.76,
"have": 7.23,
"a": 5.89,
"an": 6.54,
"apple": 7.91,
... # 其他99995个词
]
softmax层
P(\text{word}_i) = \frac{e^{\text{logits}_i}}{\sum_{j=1}^{V} e^{\text{logits}_j}}
- V: 词汇表的大小
- 指数运算:放大高分优势。
如下
"I": 0.38,
"have": 0.22,
"an": 0.18,
"apple": 0.15,
"a": 0.04,
... # 其他词概率极小
总结一下:
| 时间步 | 解码器输入 | Linear层Logits示例 | Softmax后概率 | 选定词 |
|---|---|---|---|---|
| 1 | <bos> |
I=9.8, He=1.2,... |
I=0.99,He=0.03,... |
I |
| 2 | <bos> I |
have=8.5, has=0.5,... |
have=0.97,has=0.02,.... |
have |
| 3 | <bos> I have |
an=7.9, a=2.1,... |
an=0.95,a=0.04 |
an |
| 4 | <bos> I have an |
apple=9.5, app=3.2,... |
apple=0.99,app=0.03,.... |
apple |
到这里,transformer的原理就分析完了。
参考如下:





Good job
学习了,写得不错,点赞