浅析Pi0 :VLM 与 Flow Matching 的结合之道
概述
传统机器人策略模型往往局限在单一任务或平台,难以跨场景泛化。与此同时,大规模 视觉-语言模型(VLM) 已展现出卓越的语义理解与任务指令解析能力。如果能将 VLM 的语义理解能力 与 Flow Matching 的连续动作建模能力 结合,有望构建具备泛化与实时性的机器人通用控制器。
Pi0 (π0)正是这样一个探索:基于 PaliGemma(3B 参数 VLM) 作为感知与语义主干,结合 Flow Matching 动作生成器,实现语言到多机器人动作的端到端建模。它借鉴了大语言模型的“预训练 + 微调”范式,把互联网级别的语义知识和机器人操控数据结合起来,从而实现跨平台、跨任务的通用机器人控制。
我们此前分析了VLM、Flow Matching原理,掌握这些之后理解Pi0是非常简单的。
原理
结构
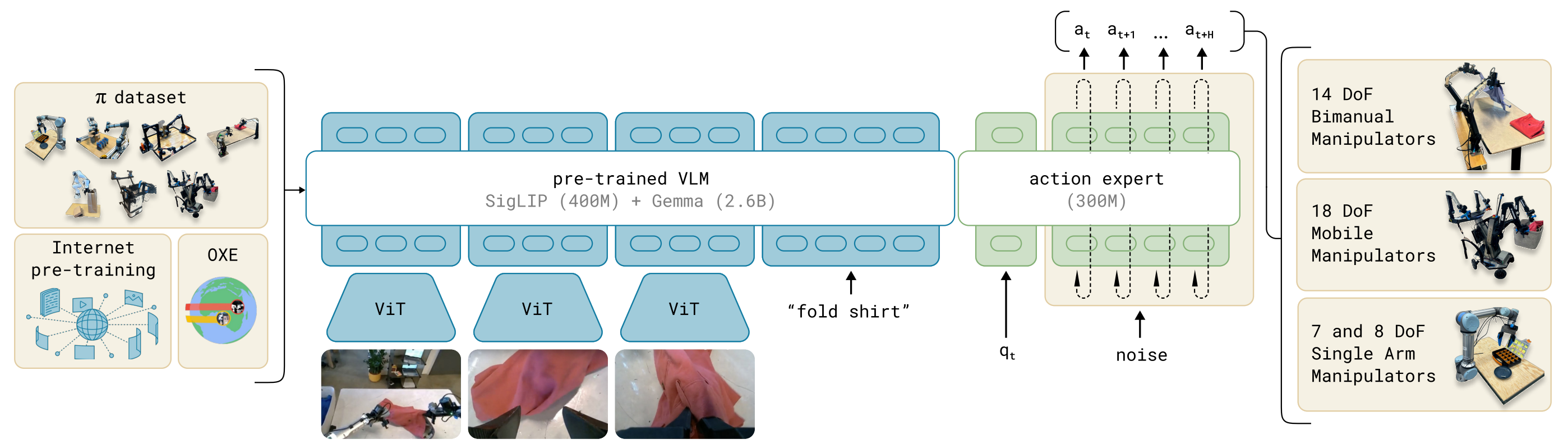
模型结构主要有VLM主干+ Action Expert动作专家构成。
- VLM主干:基于 PaliGemma(一个 3B 参数的 VLM),继承互联网规模的图像+语言知识。
- Action Expert(动作专家):额外的子网络,负责用 Flow Matching 方法预测连续动作向量。
模型的输入包括观测的多视角RGB图像、语言指令、机器人自身状态(关节角、传感器),经过模型处理后输出为高频动作序列(每秒50HZ动作chunk),这些动作控制单臂、双臂、移动操作臂等多类机器人。
训练
我们训练的目标是让A_t^0 \sim \mathcal{N}(0, I) ——>A_t(真实动作),希望模型学会如何把一个“噪声动作”流动成一个真实的动作。就像扩散模型是“噪声 → 图像”,这里是“噪声动作 → 专家动作”。
在训练的时候要让噪声动作流向真实动作,我们需要构建一个路径,这里依旧使用的是直线路径。
A_t^\tau = \tau A_t + (1-\tau)\epsilon, \quad \epsilon \sim \mathcal{N}(0,I)
这个公式跟我们在Flow Matching文章中的训练公式是不是一样的。我们在噪声动作\epsilon和真实动作A_t之间,采样一个”插值点”。\tau表示时间的进度,当\tau = 0时完全是噪声,当\tau = 1时完全是真实动作,这个就构造了一条噪声到动作的直线路径。
我们的目标是要让模型告诉我们”从当前点A_t应该往哪个方向移动,才能逐渐靠近真实动作”,因此就是在计算在每个时间速度。
u(A_t^\tau \mid A_t) \triangleq \frac{d}{d\tau} A_t^\tau
代入公式可得:
\frac{d}{d\tau} A_t^\tau = A_t – \epsilon
而论文中成u(A_t^\tau \mid A_t) = \epsilon – A_t,只是方向约定相反,本质上没有差异。上面的公式,目标速度就是噪声 – 动作,它定义了“流动的方向”。就像在地图上,目标向量场就是指路的“箭头”。这样得到了真实的速度场,我们就可以在训练的时候计算损失了。
L(\theta) = \mathbb{E}\big[ | v_\theta(A_t^\tau, o_t) – u(A_t^\tau \mid A_t) |^2 \big]
v_\theta是神经网络(Action Expert),输入 当前 noisy action + 观察o_t,输出预测的速度场。损失函数就是 预测的速度场 vs 真实的目标速度场 的均方误差 (MSE)。训练目标:让模型学会在任意中间点给出正确的“流动方向”。
推理
A_t^{\tau+\delta} = A_t^\tau + \delta v_\theta(A_t^\tau, o_t)
推理生成也比较简单,从噪声动作A_t开始,每次迭代一步:输入当前的A_t^\tau和观察的o_t,接着模型给出速度场,就沿着这个方向走一步(步长\delta),然后按照这个步骤重复迭代,最终得到真实的动作A_t。和扩散模型不同:这里不需要几十/上百步,只要 ~10 步 ODE 积分,就能得到高质量动作,适合机器人实时控制。