Flow Matching：让生成模型“流动”起来

背景

上一篇文章分析了diffusion扩散模型。diffusion扩散模型做法是加噪声、再一步步去噪，训练过程复杂，还需要 carefully 设计噪声调度。

Flow Matching提出了更直接的方式：与其通过一大堆离散的“加噪/去噪”步骤，不如直接学习一个连续的流动 (flow)，让点从噪声“顺滑地流动”到目标数据。

原理

把生成过程看作流体运动，想象有一堆水滴（噪声），通过一个力场，它们会被推动、流动，最后聚集成目标形状（真实分布的数据）。Flow Matching从物理学角度学一个”速度场”，让数据点从”源分布(噪声)”流动到”目标分布(真实数据)”。

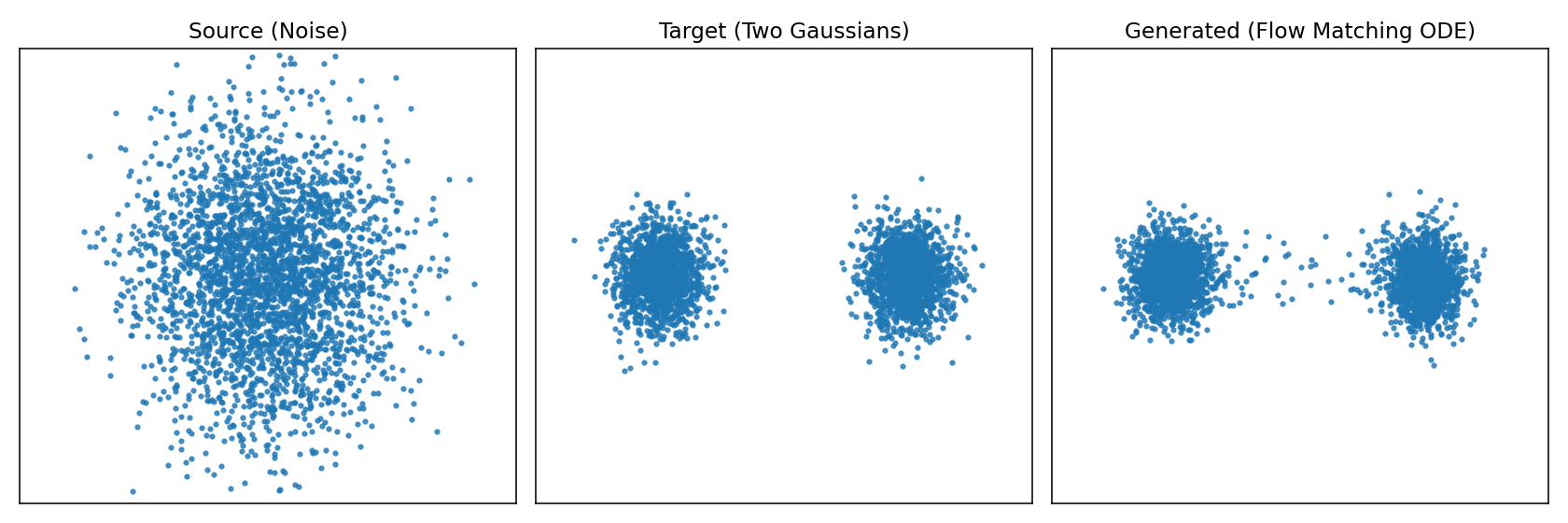
如图所示左边是源随机点云，中间是目标形状，右边是实际使用模型生成的形状。为了更直观的体会再来看下图从源分布逼近目标分布的过程。

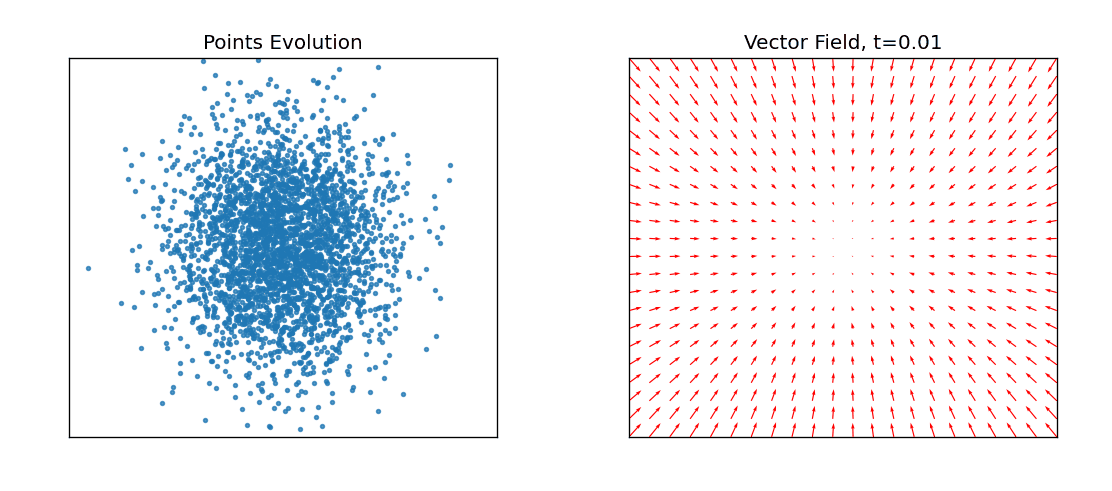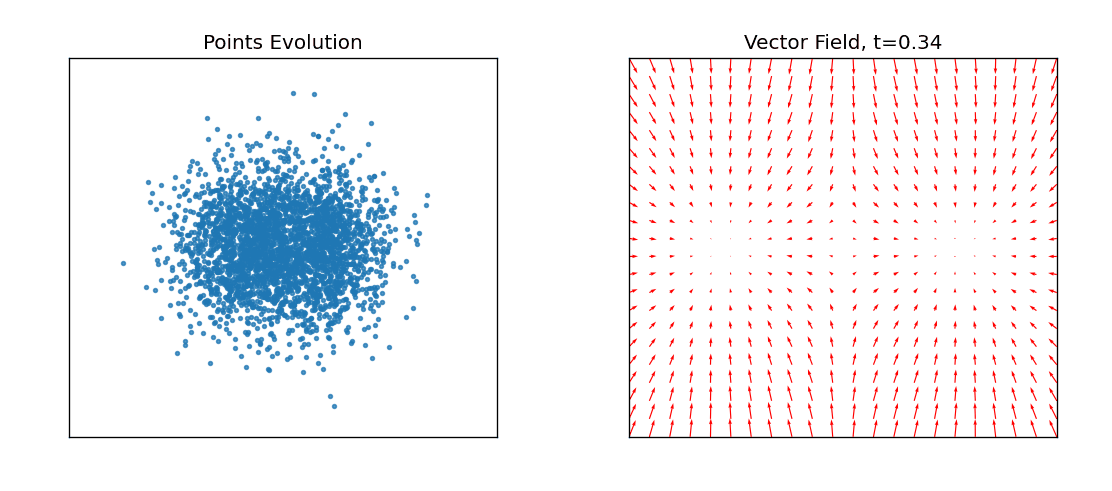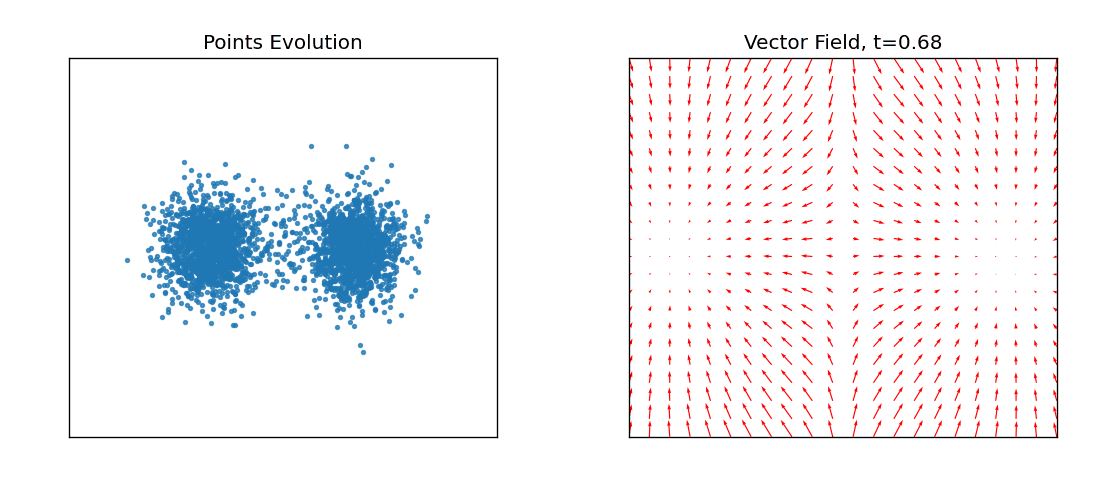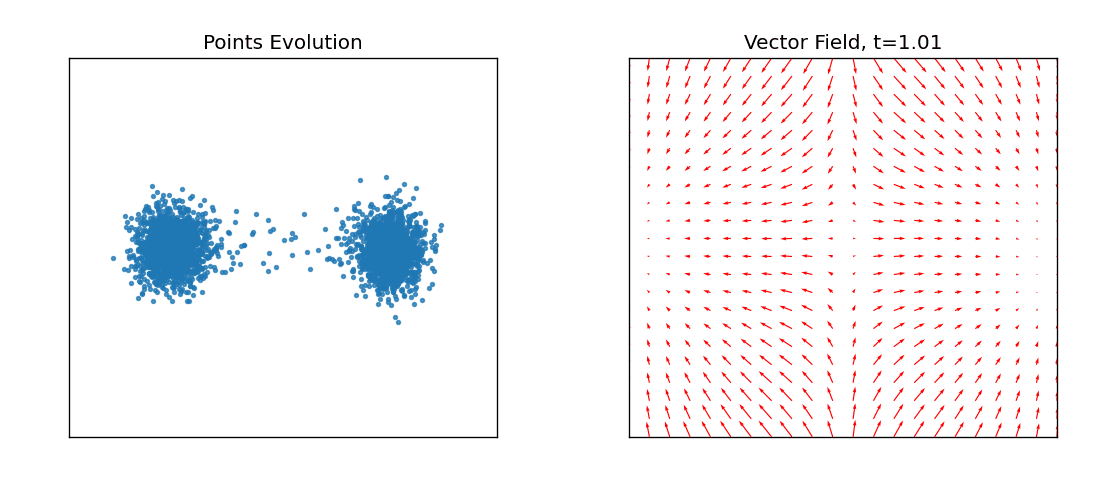
左图就是源分布的点在不同时间应该朝那个方向运动直到最终的目标分布，右图是不同时刻让这些点应该往哪个方向进行流动速度场。

接下来看看数学怎么表示，我们希望从源分布p_{src}(比如高斯分布)按照流动的方式到目标分布p_{data}，那么方式就是在每个时间t为每个点x都指定一个速度v_\theta(x,t)，这样在不同时间就知道点该往哪里动，那么点的轨迹就完全确定了。在数学上点的位置x(t)随着时间变化，那就是速度场向量，即常微分方程

\frac{dx}{dt} = v_\theta(x, t)

左边的\frac{dx}{dt}描述的是随时间的变化率，右边v_\theta(x, t)就是我们要学习的”速度场”,它给出”t时刻，位置x应该往哪里动”。

总结一下Flow Matching 里速度场写成 ODE，是因为它给出“点的位置随时间的变化率”，这正是常微分方程的定义，生成过程就是解 ODE，从噪声轨迹流到数据。

推理

模型要做的事情就是要预测出下一个时间刻应该往哪里走，输出是一个速度场；推理的过程就是解常微分方程ODE。

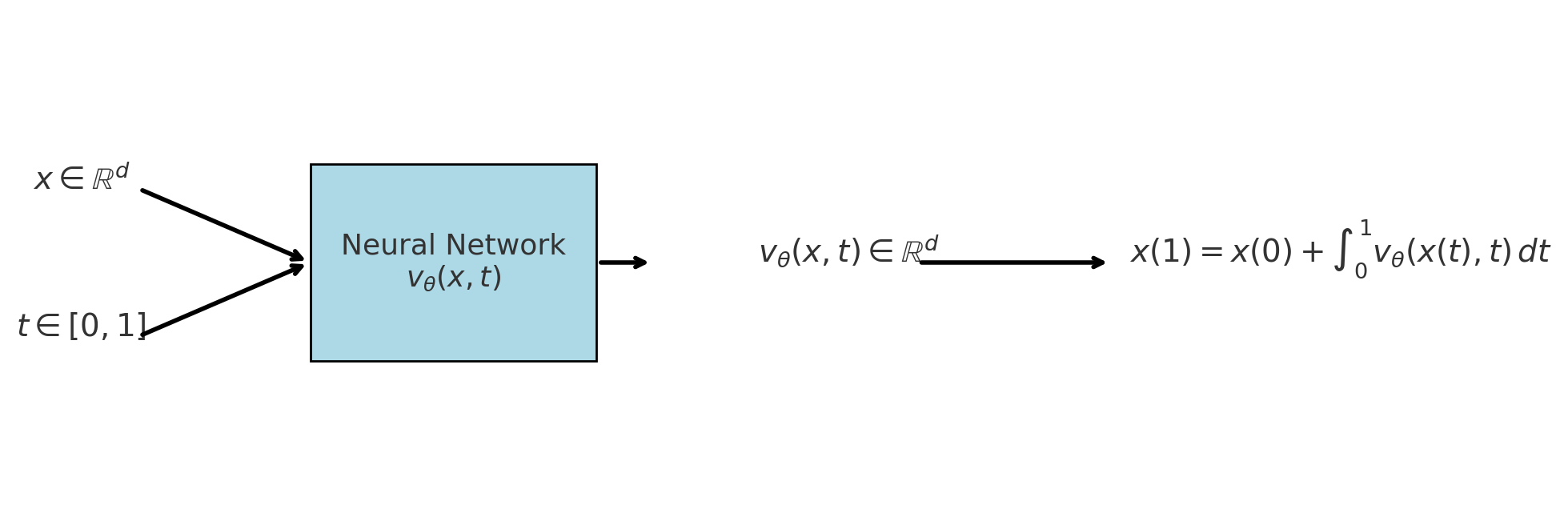
• 输入：当前位置x \in \mathbb{R}^d，当前时间t \in [0,1]。
• 输出：模型计算输出当前的速度向量，即\frac{dx}{dt} = v_\theta(x,t)。
• 更新：根据速度向量v_\theta(x,t)通过积分公式把所有时间段速度累积起来得到最终点x(1)。

x(1) = x(0) + \int_{0}^{1} v_\theta(x(t),t)\,dt

直观理解就是神经网络提供”切线方向”，积分就是”把所有切线拼起来”，形成完整的轨迹，从噪声走到目标分布。

但实际过程中我们用离散的数值方式，比如欧拉法，如下：

时间从t=0到t=1，分成若干小步（比如50或100步），在每一步按照上面公式更新。

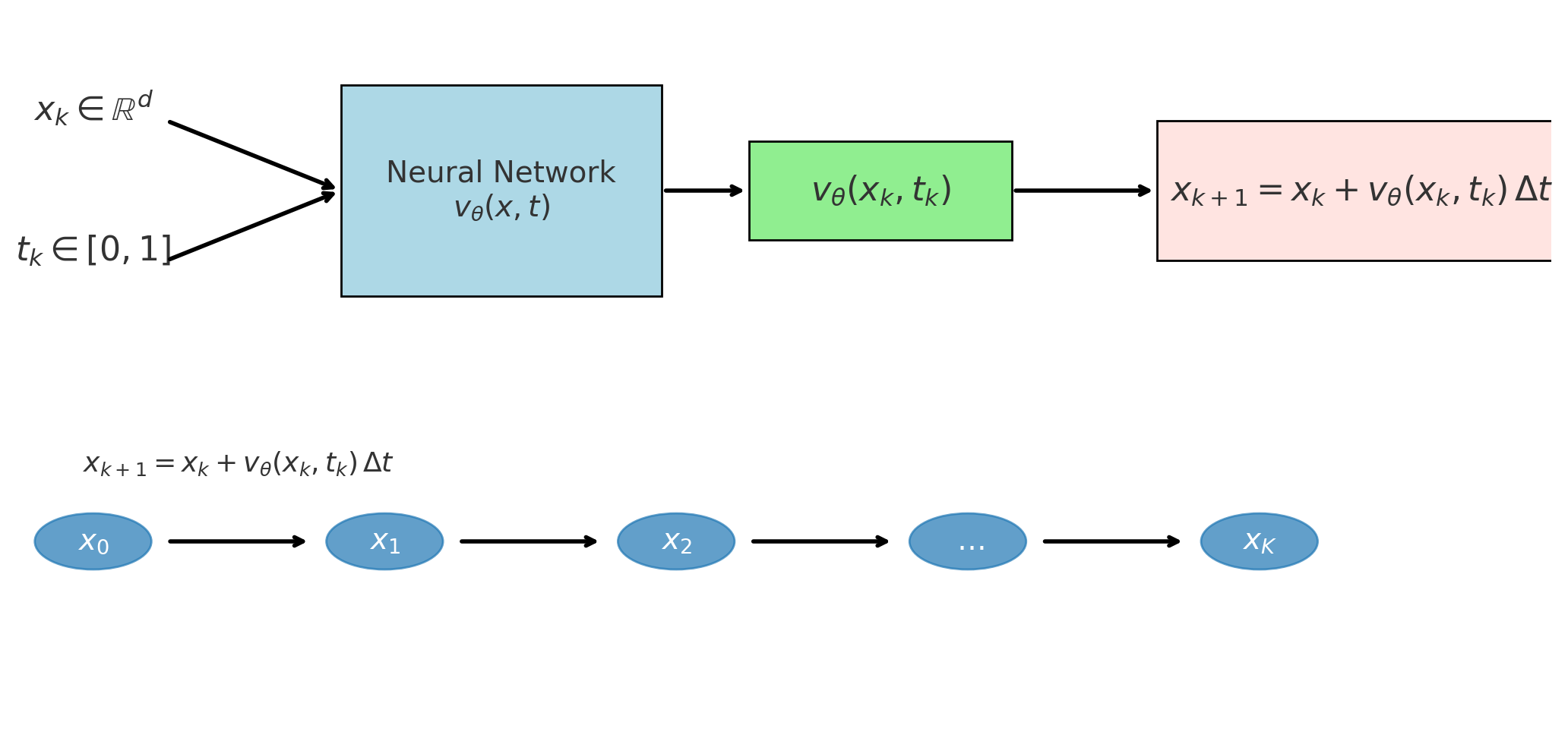
• 输入：当前的位置x_k和当前时间步t_k。
• 输出: 模型预测计算速度向量场v_\theta(x_k, t_k)。
• 更新：通过欧拉法更新公式更新下一步位置x_{k+1} = x_k + v_\theta(x_k, t_k)\Delta t

每一步模型计算出速度向量v_\theta(x_k, t_k)然后根据公式进行更新下一步的位置，新位置=旧位置+速度x时间步长；v_\theta(x_k, t_k)\Delta t计算每次迭代的移动距离（速度x时间），这就是基本的欧拉积分法，直观的意义是在短时间\Delta t内，点会沿着速度场方向前进一点。不断的进行多步迭代，从x_0出发，逐步得到x_1，x_1，x_2，x_3，….，x_k，当k=K时，t_K=1，就得到最终的x(1)。

怎么理解t_k、x_k、\Delta t？

t_k是第k步对应的时间点，如果flow matching的时间区间是[0,1]，我们把它切成K个小步（如50或100步），每个时间点就是t0=0.00，t1=0.01；\Delta t是时间步长如把时间区间[0,1]均匀分成100步，那么\Delta t=1/100=0.01；x_k是表示在t_k时的点（或点云），初始时从高斯噪音采样到。

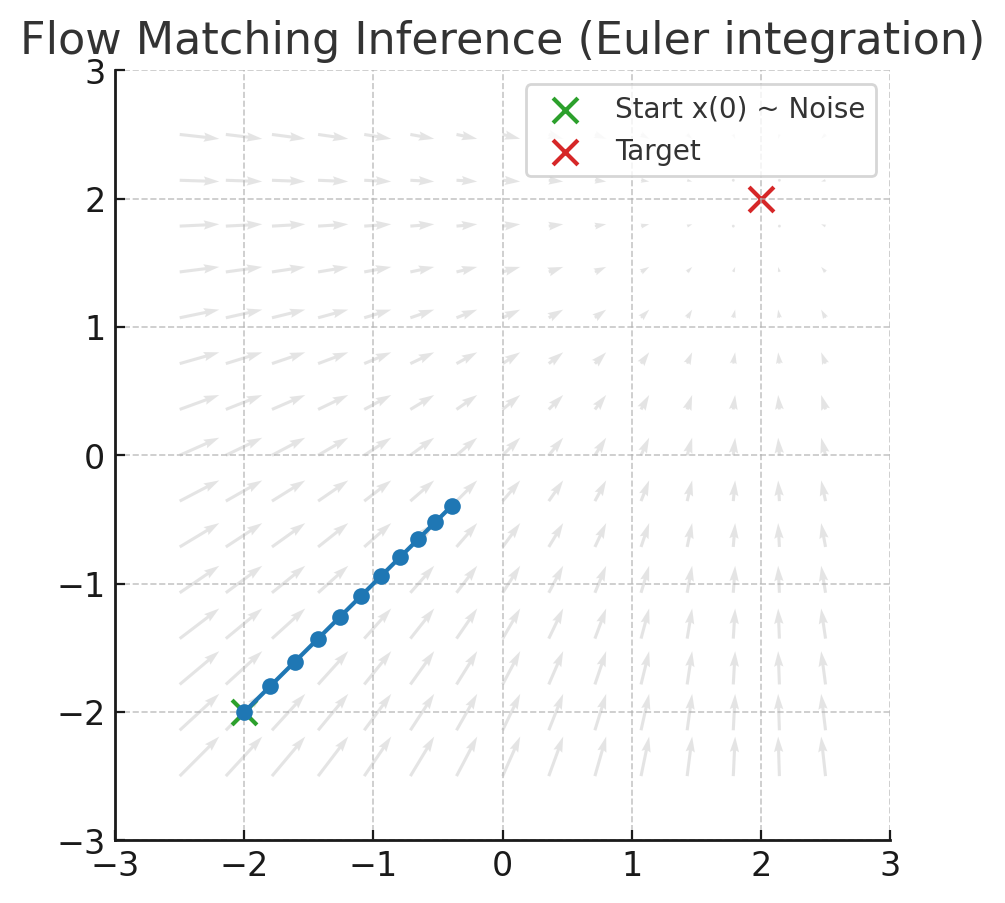
下面再来一个直观图展示了Flow Matching推理的过程。

• 灰色箭头：代表速度场v_\theta(x_k, t_k)，告诉每个位置的点应该往哪里走。上图设定的目标是(2,2)。
• 绿色点：初始x(0)来自噪声分布即源分布。
• 红色叉：表示目标位置，代表数据分布的一个样本区域。
• 蓝色折现轨迹：数值积分结果，点一步一步验证速度场北推向目标。

训练

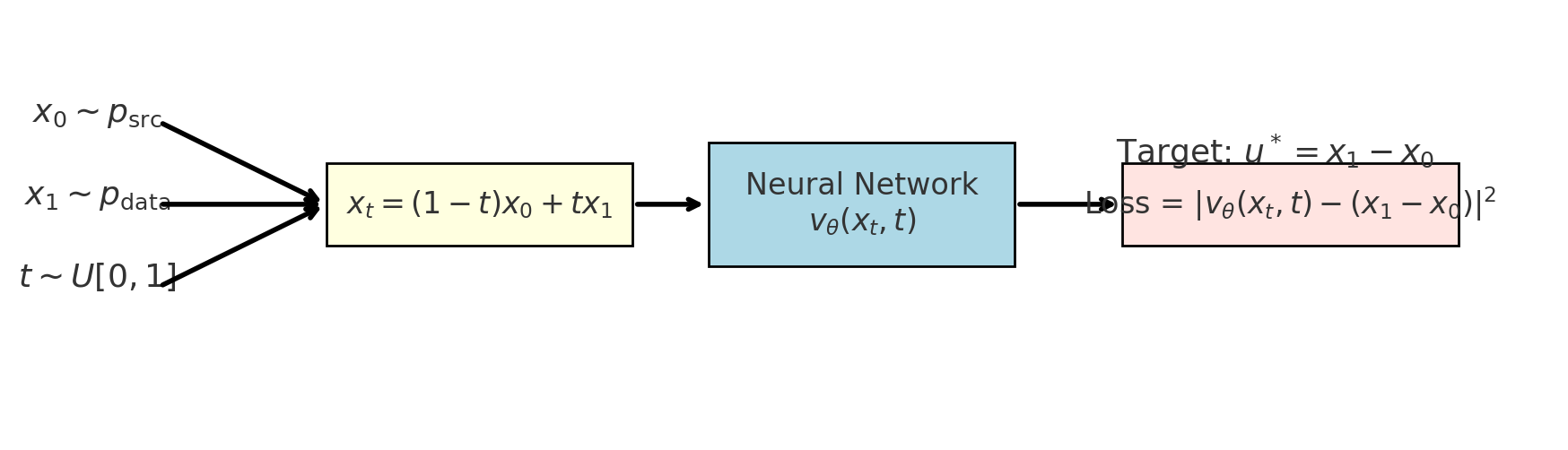
我们希望模型学会把源分布p_{src}流动到目标分布p_{data}；换句话说就是有x_0 \sim p_{\text{src}}，输出目标点x_1 \sim p_{\text{data}}我们要训练一个速度场网络v_\theta(x_k, t_k)，让它指导点x_t沿正确的路径从x_0——>x_1。

要训练行动轨迹需要知道真实轨迹这样才能和实际预测值做比较求损失，而训练的关键却正好是不知道真实的速度场。那如何构建训练的目标了？可以设计一个简单的”参考轨迹”，如直线路径x_0——>x_1。

x_t = (1 – t)x_0 + tx_1

给定输入样本(x_0 \sim p_{\text{src}},x_1 \sim p_{\text{data}})，其中x_0是源随机位置，x_1是目标位置。在训练的时候我们自己定义一条直线路径x_0——>x_1，我们不能一步到位，而是要有一个流动的过程。

这条直线路径上的真实速度公式对t求偏导，而恰巧速度是一个常数（始终指向目标点x_1）。

u^\star = \frac{dx_t}{dt} = x_1 – x_0

既然速度方向就是一个常数x1-x0，为什么不直接一步把x1变成x0，而要搞成连续流动了？

如果一步到位公式就变成x_1 = x_0 + (x_1 – x_0)，相当于直接跳到目标点，完全不需要ODE、积分、网络。但问题在于训练时我们有配对的(x_0, x_1)，所以能写下(x_1-x_0)，而推理时了我们只有x_0 \sim p_{\text{src}},并不知道该对应那个x1，因此不能一步到位，因为没有x_1可直接计算。

最后我们训练目标就是网络预测的速度v_\theta(x_k, t_k)，损失就网络预测的速度v_\theta(x_k, t_k)与真实的速度x_1-x_0的均方误差。训练完成之后，网络就学会了在任何位置x_t、时间t给出正确的速度场。

\mathbb{E}\Big[ || v_\theta(x_t, t) – (x_1 – x_0) ||^2 \Big]

源码示例

为了加深理解，程序实现一个最小的 Conditional Flow Matching（直线路径的 Rectified Flow）示例，学习时间条件速度场 vθ(x,t)，把二维标准高斯源分布推到左右两个高斯簇的目标分布。训练后输出两张图：训练损失曲线 cfm_loss.png，以及三联静态图 cfm_overview.png（源/目标/生成）。

# -*- coding: utf-8 -*-
# Flow Matching demo: source N(0,I) -> target: Two Gaussians (left & right)
# 输出：
#   1) cfm_loss.png（训练损失）
#   2) cfm_overview.png（三联图：Source / Target / Generated）
# 依赖：pip install torch matplotlib

import time, warnings
warnings.filterwarnings("ignore", category=UserWarning, module="matplotlib")

import numpy as np
import torch, torch.nn as nn, torch.optim as optim

import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt

# ------------------------- 配置 -------------------------
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
torch.manual_seed(0)
XLIM = (-4.0, 4.0)
YLIM = (-3.0, 3.0)

# ------------------------- 数据分布 -------------------------
def sample_source(n):
    return torch.randn(n, 2, device=device)

def sample_target(n):
    sigma = 0.35
    means = torch.tensor([[-2.0, 0.0], [2.0, 0.0]], device=device)
    idx = torch.randint(0, 2, (n,), device=device)
    mu = means[idx]
    return mu + sigma * torch.randn(n, 2, device=device)

# ------------------------- 模型：速度场 v_theta(x,t) -------------------------
class VelocityNet(nn.Module):
    def __init__(self, h=64):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(3, h), nn.ReLU(),
            nn.Linear(h, h), nn.ReLU(),
            nn.Linear(h, 2),
        )
    def forward(self, x, t):
        return self.net(torch.cat([x, t], -1))

# ------------------------- 训练（CFM，直线路径） -------------------------
def train_cfm(steps=2000, batch=512, lr=1e-3):
    net = VelocityNet().to(device)
    opt = optim.Adam(net.parameters(), lr=lr)
    loss_hist = []
    t0 = time.time()
    for s in range(1, steps + 1):
        x0 = sample_source(batch)
        x1 = sample_target(batch)
        t  = torch.rand(batch, 1, device=device)
        xt = (1 - t) * x0 + t * x1
        u  = x1 - x0

        pred = net(xt, t)
        loss = ((pred - u)**2).mean()

        opt.zero_grad(set_to_none=True)
        loss.backward(); opt.step()
        loss_hist.append(float(loss))

        if s % 200 == 0:
            print(f"[{s}/{steps}] loss={loss:.4f}")
    print(f"Train time: {time.time() - t0:.2f}s")
    return net, loss_hist

# ------------------------- 采样（生成轨迹） -------------------------
@torch.no_grad()
def generate_traj(net, n=3000, steps=60):
    x = sample_source(n)
    dt = 1.0 / steps
    traj = [x.cpu().numpy()]
    for k in range(steps):
        t = torch.full((n,1), (k + 0.5) * dt, device=device)
        x = x + net(x, t) * dt
        traj.append(x.cpu().numpy())
    return traj

# ------------------------- Matplotlib 工具 -------------------------

def save_loss(loss_hist, path):
    plt.figure(figsize=(6, 3.6))
    plt.plot(loss_hist)
    plt.title("Training Loss (CFM)")
    plt.xlabel("step"); plt.ylabel("MSE")
    plt.tight_layout(); plt.savefig(path, dpi=140); plt.close()
    print(f"Saved {path}")

def save_overview(src, tgt, gen, path):
    fig, axes = plt.subplots(1, 3, figsize=(12, 4))
    titles = ["Source (Noise)", "Target (Two Gaussians)", "Generated (Flow Matching ODE)"]
    for ax, title, pts in zip(axes, titles, [src, tgt, gen]):
        ax.scatter(pts[:, 0], pts[:, 1], s=5, alpha=0.75)
        ax.set_title(title)
        ax.set_xlim(*XLIM); ax.set_ylim(*YLIM)
        ax.set_xticks([]); ax.set_yticks([])
    plt.tight_layout(); plt.savefig(path, dpi=140); plt.close()
    print(f"Saved {path}")

# （已移除 GIF 相关工具与依赖）

# ------------------------- 主程序 -------------------------
if __name__ == "__main__":
    # 训练
    net, loss_hist = train_cfm(steps=2000, batch=512, lr=1e-3)
    save_loss(loss_hist, "cfm_loss.png")

    # 数据与生成
    src = sample_source(3000).cpu().numpy()
    tgt = sample_target(3000).cpu().numpy()
    traj = generate_traj(net, n=3000, steps=60)
    gen = traj[-1]

    # 三联静态图
    save_overview(src, tgt, gen, "cfm_overview.png")

    # （已移除 GIF 生成步骤）

    print("All done.")

（1）模型结构

模型结构为VelocityNet，使用了一个小型 MLP，输入 3 维（x 的 2 维 + t 的 1 维），输出 2 维速度向量。结构为Linear(3,64) → ReLU → Linear(64,64) → ReLU → Linear(64,2)。forward(x,t) 直接拼接 [x, t] 后送入网络。这里没有使用时间位置编码。

（2）训练过程

训练函数为train_cfm(steps=2000, batch=512, lr=1e-3)，具体过程如下：

1) 每步采样源 x0 ~ source 和目标 x1 ~ target，独立均匀采样 t~U(0,1)。
2) 构造直线桥接点 xt = (1 – t)x0 + tx1。
3) 定义理想恒定速度 u = x1 – x0（常速，不依赖 t）。
4) 让网络在 (xt, t) 上预测 pred = vθ(xt,t)，用 MSE(pred, u) 作为损失。
5) Adam 更新一次；每 200 步打印当前损失。
6) 返回训练好的 net 与 loss_hist。

直观理解，虽然 u 依赖 (x0, x1)，但模型只观察 (xt,t)。训练学到的是条件期望 E[x1 – x0 | xt, t]，也就是让网络在直线路径上学会把点往“正确方向”推的平均速度。这是直线路径 CFM 的核心思想。

（3）采样

采样函数为generate_traj，从源分布采样 n 个起点，设步长 dt=1/steps。用无梯度模式按欧拉法更新：对每步 k，用中点时间 t=(k+0.5)dt 预测速度 vθ(x,t)，然后 x ← x + vθ(x,t)dt。记录每一步的点云到列表，返回整个轨迹（列表元素是 numpy 数组）。主程序中只使用最后一步作为“生成结果”。

（4）主流程

最后就是主流程先调 train_cfm 进行训练，保存 cfm_loss.png。分别采样 3000 个源样本 src 与目标样本 tgt。生成 n=3000、steps=60 的轨迹 traj，并取 gen = traj[-1] 作为最终生成样本。保存 cfm_overview.png，展示源/目标/生成的对比。

整体主要的实现点为

• 目标路径：x_t = (1 – t) x0 + t x1，直线连接源与目标。
• 理想速度：dx/dt = x1 – x0，使点沿直线以恒定速度匀速前进。
• 学习目标：在 (xt,t) 上回归 u = x1 – x0 的条件期望；推断时只需网络与当前状态，无需知道具体的 x0 或 x1。
• 数值积分：使用欧拉法简单高效；采用中点时间能略微减小离散误差。