轻量SmolVLA:半层VLM、视觉压缩与异步推理赋能具身智能
概述
SmolVLA 是一套轻量级视觉-语言-行动(VLA)策略:前端用小型 VLM(视觉 SigLIP + 语言 SmolLM2)做感知与理解;后端用一个“动作专家”专门预测一段连续的低层控制。它与Pi0相比,参数规模少了将近10倍只有约0.45B(450M)。它的目标是在低算力下也能稳定执行多任务机器人控制,并保持接近甚至超过更大模型的效果。
SmolVLA 通过冻结 VLM、只训练动作专家(Action Expert),再配上四件“硬核小技巧”——取 VLM 的前半层、把每帧视觉 token 压到 64、以及Self-Attn—>Cross-Attn交替方式、异步推理;在大幅降算力与时延的同时,保持/逼近甚至超过更大模型的性能;注意力计算交替方式让动作专家既能不断获取外部视觉/语言指导,又能在内部序列里建立自己的时序与物理一致性,从而在算力可控的前提下提升稳定性和表现;提供异步执行,把“算下一段动作”和“执行当前动作”并行起来,显著减少空窗时间。
原理
结构
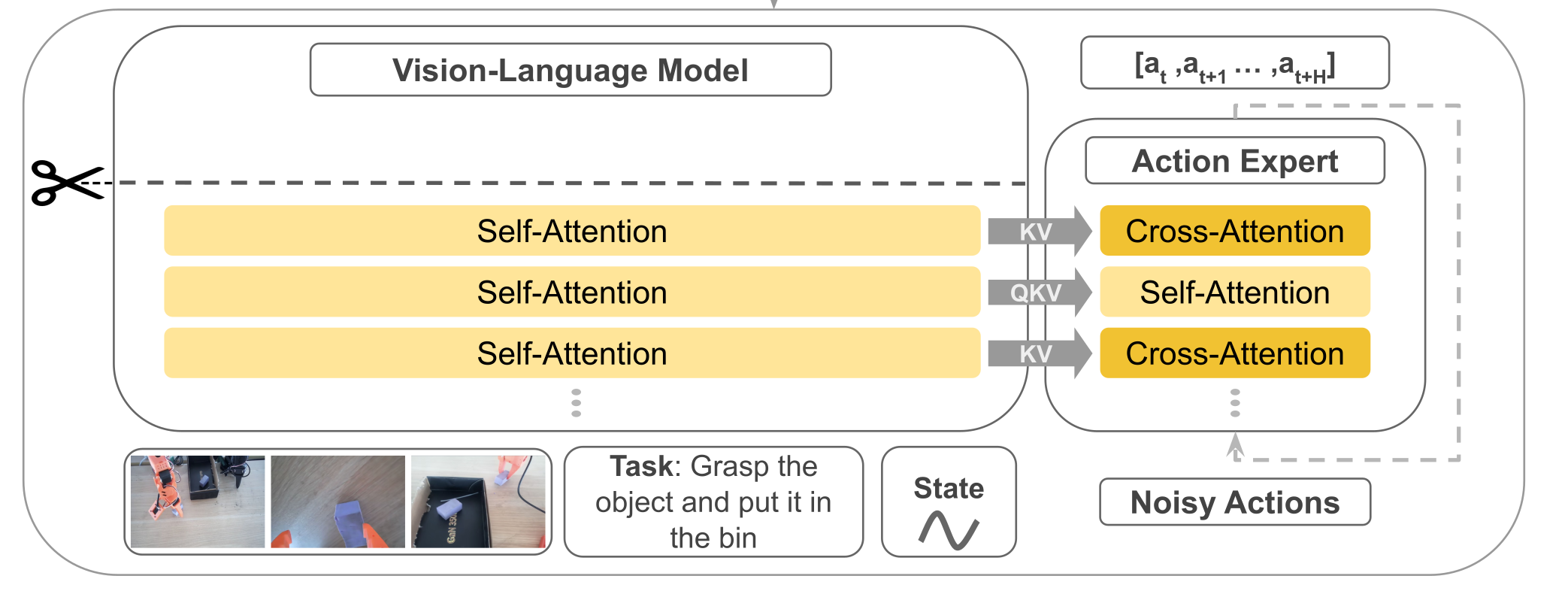
其模型结构主要有前端的VLM+后端的动作专家Action Expert组成,结构组成与Pi基本一致但实现方式有很大差异不同。先总结一下组件,稍后我们在稍作展开补充。
- 输入:文本指令token+视觉token(多摄像头采集的图像)+机器的状态(关节角、传感器)。
- VLM(感知端):采用SmolVLM-2,VLM共有L层,但是只N=⌊L/2⌋层隐藏表示喂给动作专家。
- Action Expert(控制端):一个Flow Matching Transformer,以以Cross → Causal Self → Cross 的“三明治”层为基本单元,按块预测n步动作序列。
- 输出:一次预测长度为n的动作块,对应机器的控制指令。
SmolVLA与Pi0有很多相似之处,不过其背后有四个关键设计,分别是Layer Skipping(层跳过)、Visual tokens reduction(视觉token压缩)、动作专家交替Self-Attn与Cross-Attn、异步推理。本小节先围绕前面3部分进行解析,异步推理于后续章节展开。
(1)Layer Skipping
层跳过就是把感知端的VLM(视觉+语言)的解码器中间层拿来当条件特征,而不是等它把整个层都计算完再输出;具体的做法就是只去N=L/2层的隐藏层表示送给动作专家,VLM权重冻结不训练。之所以要这样做经验规律表示(论文中作者提到)深层 LLM 层更偏“词级生成/长链路语义”,而中层已经集中了“指令 + 视觉”的对齐语义,对控制足够;继续往后让语言头生成 token 既耗算,又不是控制必须。前半层就停下,少算一半的自注意 + MLP,显存开销也随之下降。
大概得实现是把“文本指令 token、图像 token、状态 token”拼接,送入解码器;在第N层获取特征信息H然后用一个线性投影到Action expert所需的维度d_a作为K/V。如果在长时、极强推理型任务(需要深层语言生成)时可以适当调大N。
(2)视觉token压缩
在transformer里面,“token”就是序列里的一个位置。对图像来说,我们把一张图拆成很多小块(patch)或网格上的特征点,每个块/点用一个向量表示,这个向量就是视觉 token(不明白的可以看看ViT原理解析介绍)。视觉token压缩具体的做法是保整图、不裁块,把空间上密的token折叠到通道里,从而让token数变少。
设 ViT patch 后得到的特征图大小为 \frac{H}{p} \times \frac{W}{p} \times d,选一个下采样因子 r (整数),做 space-to-depth:
\underbrace{\frac{H}{p} \times \frac{W}{p}}_{\text{原网格}} \xrightarrow{\div r} \underbrace{\frac{H}{pr} \times \frac{W}{pr}}_{\text{更稀疏的网格}}, \quad
\underbrace{d}_{\text{通道}} \xrightarrow{\times r^2} \underbrace{d \cdot r^2}_{\text{更厚的通道}}
计算示例:
- 输入尺寸:512 \times 512 图像
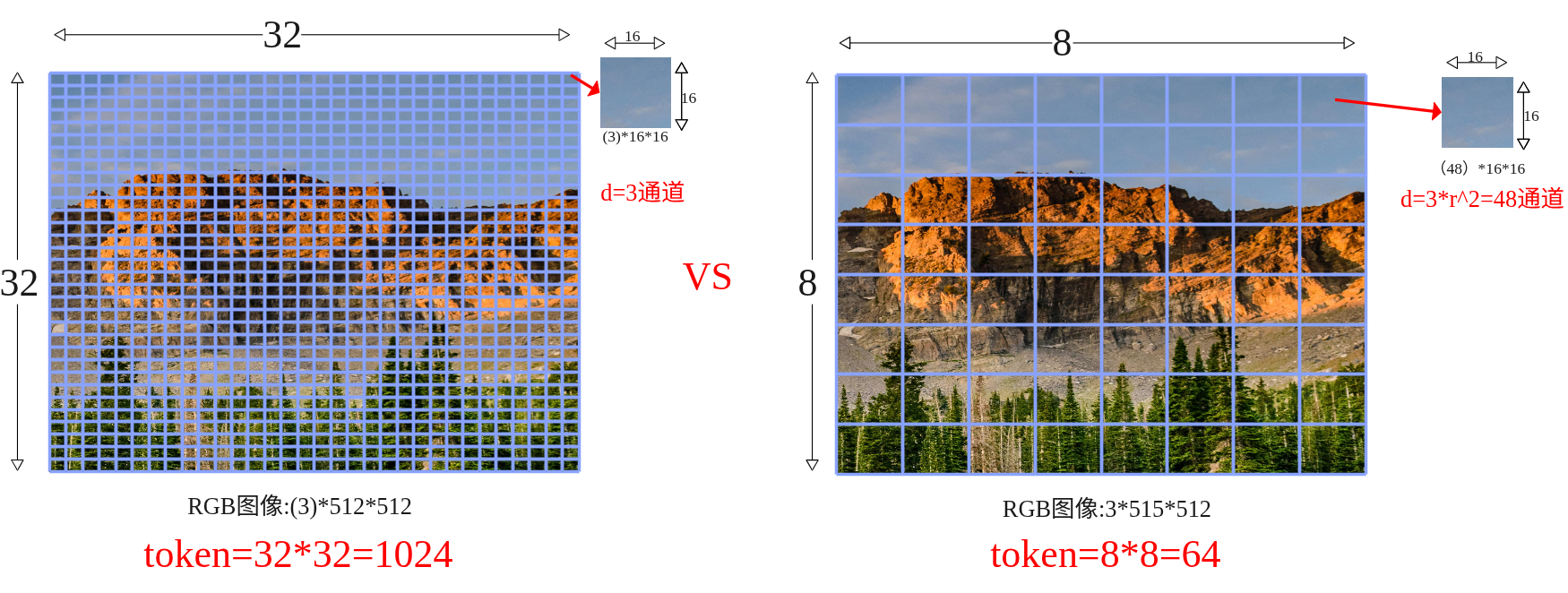
- Patch大小 p=16 ⇒ 32 \times 32 token网格
- 选r=4 ⇒ \frac{32}{4} \times \frac{32}{4} = 8 \times 8 网格
- Token数:8 \times 8 = 64(减少4^2=16倍)
- 通道维度:d=3 \rightarrow d=3 \times 16=48
可以看到如果是按照ViT的默认方式patch数量为32×32=1024,每个patch的维度为3x16x16=768,然后如果输入编码的d_mode=512那么经过线性投影变成矩阵(1024,512),即1024个token数量,每个token维度是512;而如果进行压缩后patch数量为8×8=64,每个patch的维度为48x16x16=12288,经过线性投影后变成(64,512)即64个token,每个维度是512。这里也可以看到原来是768降为到512,压缩的是从12288降维到512,降得比较猛,效果真的没有衰减吗?
总结一下smolvla在视觉token上进行了压缩,使用space-to-depth,对于512X512的图每帧token从1024降低到了64帧,如ViT的patch操作后得到的特征图维度为\mathbb{R}^{\frac{H}{p} \times \frac{W}{p} \times d},选择下采样因子 r(整数)进行space-to-depth操作:
\mathbb{R}^{\frac{H}{p}\times\frac{W}{p}\times d}
\xrightarrow{\text{S2D}_{r}}
\mathbb{R}^{\frac{H}{pr}\times\frac{W}{pr}\times(d\cdot r^{2})}
这样token数减少r^{2}倍,把细节挪到通道数去。
(3)动作专家交替Self-Attn与Cross-Attn
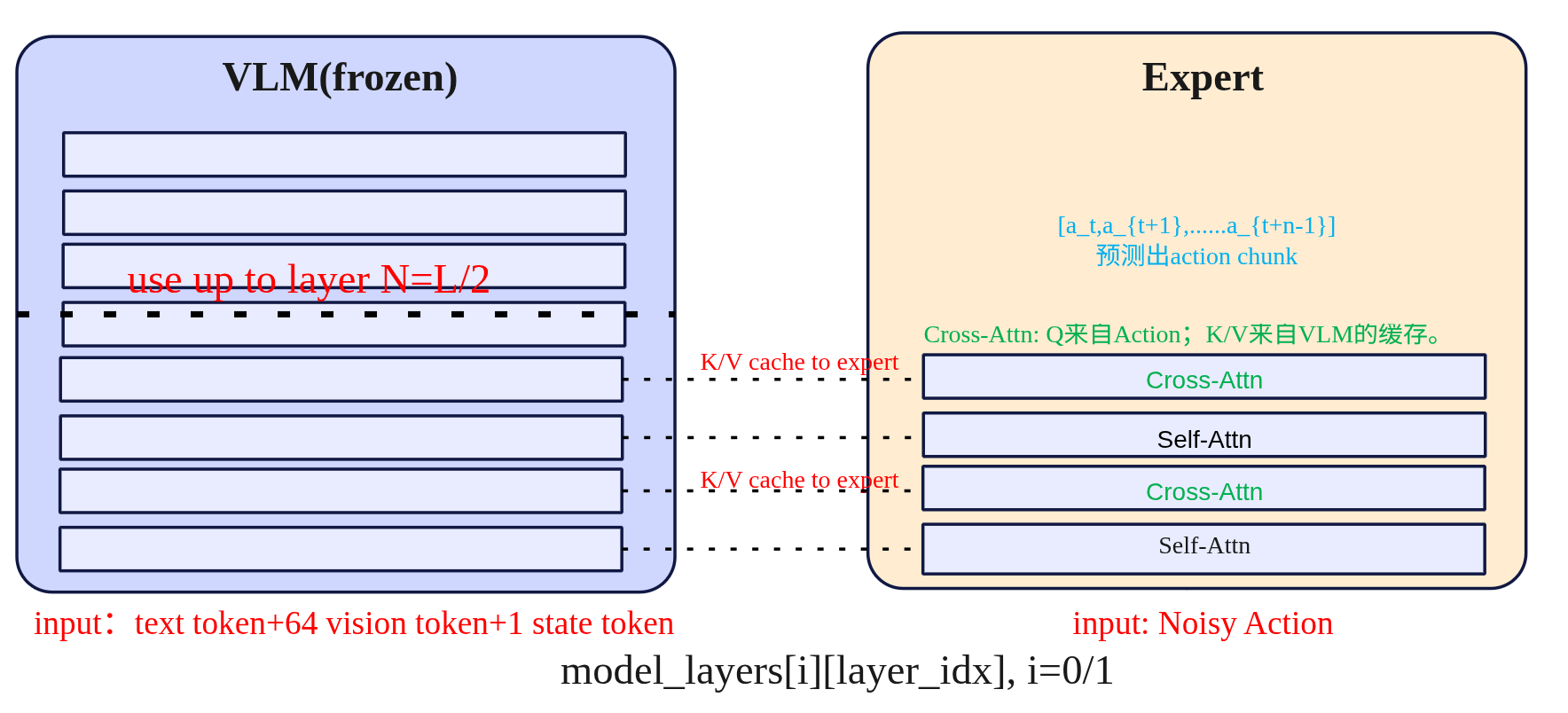
在动作专家中使用了交叉注意力机制,具体的排布可以配置。VLM的每一层与右边的Expert是一一对齐的,当然也可以配置Expert模型只有VLM层数的一半,每两层VLM才有一层Expert,那么其中VLM对齐层将为NONE,下图以VLM和Expert都为4层来示例交替注意力的实现。
- Self-Attn(管自己,守时序):只允许第 i 步看 ≤i 的历史步(因果掩码),在动作序列内部传播动力学与约束,做轨迹的时间一致性与平滑。这一步相当于“内化刚才读到的证据”并让各步动作彼此协调。在计算注意力时,会将VLM的QKV与Expert的QKV进行拼接起来一起送入transformer计算,但通过掩码保证 VLM 的Q只看自己(不去读 Expert),而 Expert 的 Q 可以访问 VLM 的 K/V(即“读”VLM 语义),这样既提供了计算效率也提升了Expert的语义丰富性。
- Cross-Attn(看环境,取证):看环境取证,让每个动作 token 先从条件特征里“读”一遍(条件=VLM中间层输出,含文本指令+多路视觉+状态)。这样动作表示一开始就被场景锚定,知道当下该关注哪里/哪件物体。具体是交叉注意力计算Q来自Expert Action自己,而K/V 来自 VLM 对应层的输出缓存。
训练
目标让动作专家 在观测条件 o_t 下输出v_\theta速度场,把“噪声动作”沿路径推向真实动作块 A_t。这里跟Pi0和Flow Matching是一样大同小异,就简要说明一下。
- 观测条件:o_t=H^{(N)}\in\mathbb{R}^{T\times d_o}\ \xrightarrow{\text{proj}}\ O_N\in\mathbb{R}^{T\times d_a}(VLM 冻结;O_N 作为 Cross-Attn 的 K/V)。
- 真实动作块:A_t\in\mathbb{R}^{n\times d_{\text{act}}}(建议标准化/白化)。
- 噪声:\varepsilon\sim\mathcal N(0,I)(同形)。
- 路径时间:\tau\sim\mathrm{Beta}(\alpha,\beta)。这里与Pi0不同。
路径与目标速度场:
A_t^{\tau}=\tau A_t+(1-\tau)\varepsilon,\left(A_t^{\tau}\mid A_t\right)=\varepsilon-A_t
计算损失函数:
\mathcal{L}^{\tau}(\theta) = \mathbb{E}_{p\left(\mathbf{A}_{t} \mid \mathbf{o}_{t}\right), q\left(\mathbf{A}_{t}^{\tau} \mid \mathbf{A}_{t}\right)}
\left[
\left||
\mathbf{v}_{\theta}\left(\mathbf{A}_{t}^{\tau}, \mathbf{o}_{t}\right) – \mathbf{u}\left(\mathbf{A}_{t}^{\tau} \mid \mathbf{A}_{t}\right)
\right||^{2}
\right]
这里 ||\cdot||^{2} 表示欧氏范数平方;实现即逐元素 MSE。
为提升推理效率,动作专家隐藏宽度取 d_a=0.75\times d(d 为 VLM 的隐藏宽度)。
以下是一个简单的示例,可看看过程理解一下。
# 条件:取 VLM 第 N 层隐藏(冻结)
with torch.no_grad():
H = vlm_hidden_at_layer_N(obs_tokens) # [T, d_o]
KV = proj(H) # [T, d_a] 供 Cross-Attn 作 K/V(可缓存)
# 构造路径与目标速度
A = sample_action_chunk() # [n, d_act] (已标准化)
eps = torch.randn_like(A) # [n, d_act]
tau = Beta(alpha, beta).sample(()).to(A.device)
A_tau = tau * A + (1 - tau) * eps
u = eps - A
# 前向与损失
pred = v_theta(A_tau, KV) # 与 u 同形
loss = F.mse_loss(pred, u) # 对应 ||·||^2
loss.backward(); optimizer.step(); optimizer.zero_grad()
推理
在SmolVLA提到了异步推理,先来看看同步推理。
- 取最新观测 → 得到 O_N;
- 以噪声初始化,做 K\approx10 步显式积分(Euler/Heun)得到一个动作块 [a_t,\dots,a_{t+n-1}];
- 执行动作块 → 重复。
同步(sync)推理一次性生成长度为 n 的动作队列(chunk)A_t=\big[a_t,\dots,a_{t+n-1}\big],执行完再用新观测预测下一段。执行与推理串行,会产生“空窗”(执行停下等待推理)。而异步(async)推理是解耦“动作执行”和“动作预测”。机器人端持续消费现有队列;当队列余额低于阈值就异步把当前观测发给策略端预测“下一段”,回来后与旧队列重叠拼接。这样执行与推理并行,显著降低总时延,同时仍保持接近的成功率。
异步推理在架构上可以分为两个部分:
- RobotClient(机器人端):以控制周期 \Delta t 持续下发队列头部动作;本地维护动作队列 A_t 与触发逻辑;可做相似度过滤(见下节)。
- PolicyServer(策略端):接收观测 o_t,运行策略 \pi 预测新队列 \tilde A_{t+1} 后返回;可放在更强的远端算力(GPU/工作站/云)。
看看论文中给出的算法实现:
设时域 T、段长 n、触发阈值 g\in[0,1]。
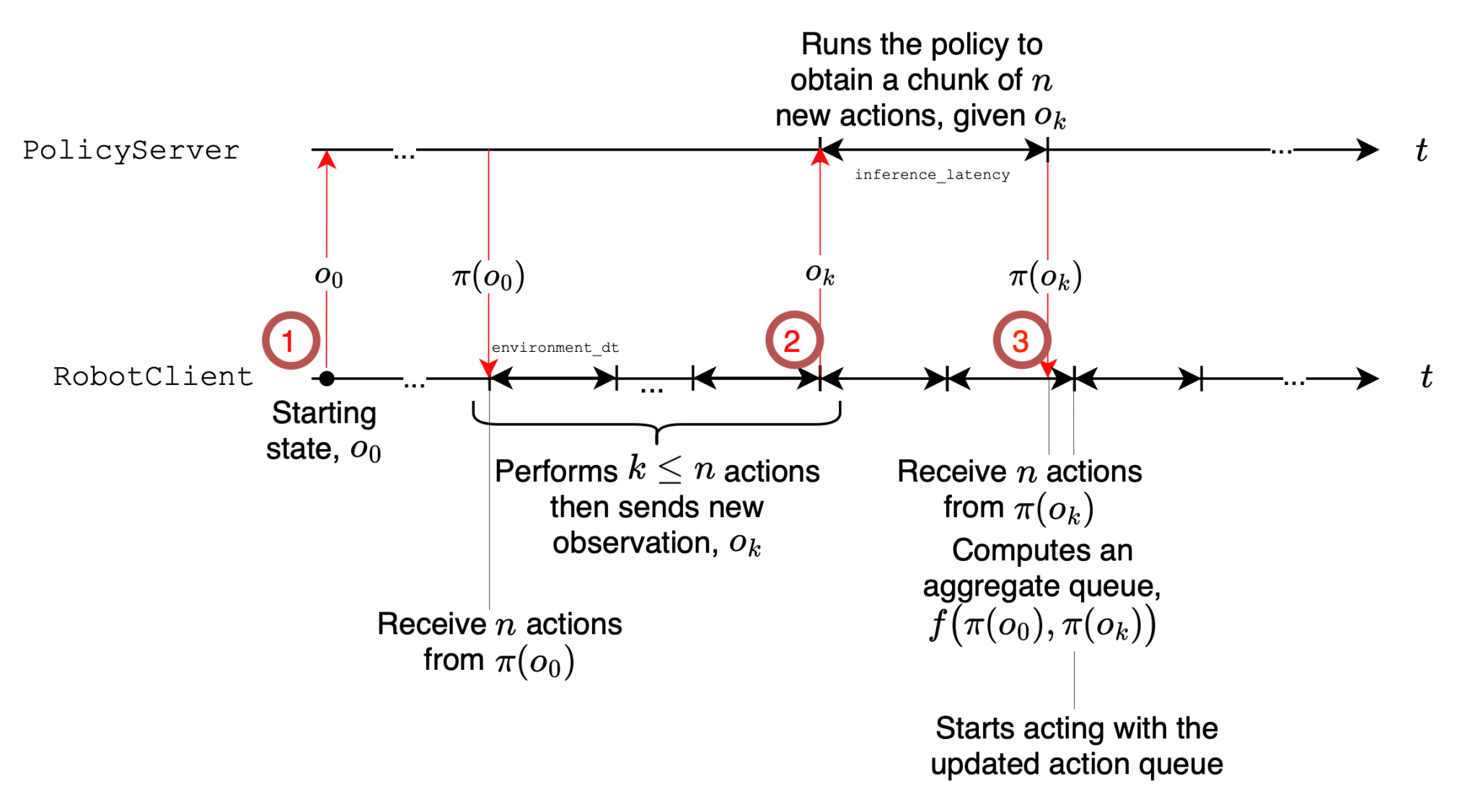
- 初始化:采集 o_0,发送到策略端,得到首段 A_0\leftarrow\pi(o_0)。
- 主循环 对 t=0\dots T:取出并执行一步 a_t\leftarrow\text{PopFront}(A_t);若 队列余额占比 \dfrac{|A_t|}{n}<g,采集新观测 o_{t+1};若 NeedsProcessing(o_{t+1}) 为真(见“相似度过滤”),则异步触发:①发送 o_{t+1} 到策略端,得到新段 \tilde A_{t+1}\leftarrow\pi(o_{t+1})(异步返回);②用重叠拼接函数 f(\cdot) 合并:A_{t+1}\leftarrow f(A_t,\tilde A_{t+1});若本轮异步推理尚未结束:A_{t+1}\leftarrow A_t(继续消费旧队列)。
论文中的 NeedsProcessing 用于避免重复观测触发;f 表示对重叠步的拼接(线性渐入/平滑器等,见下重叠拼接(Overlap & Merge))。
关键触发量,队列余额阈值 g:
- 触发条件:当 \dfrac{|A_t|}{n}<g 时触发一次异步预测。
- 直觉:g 越大,越提前触发,越不容易见底;但也会更频繁地调用策略端(算力/网络开销更高)。
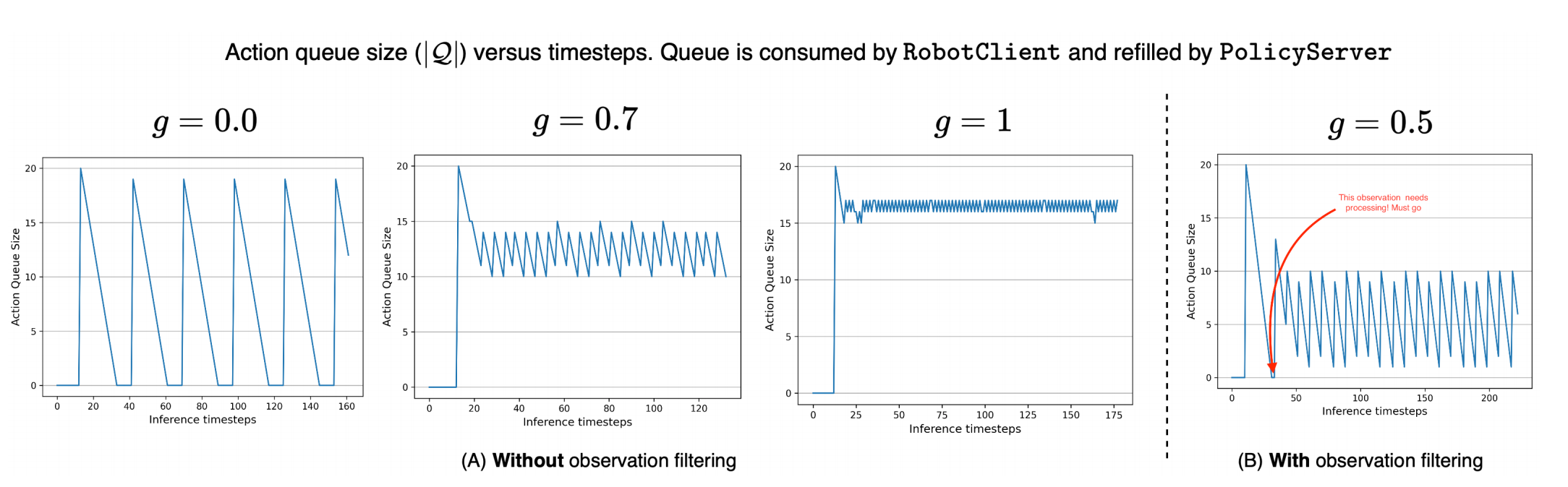
- 论文的三个代表场景:g=0(顺序极限):耗尽队列才发起新预测 → 一定出现空窗等待;g=0.7(典型异步):每段大约消耗 1-g=0.3 的比例就触发,计算摊在执行过程中,队列不见底;g=1(计算密集极限):步步都发观测 → 几乎“满队列”,反应最快但计算最贵(等同每个 tick 都前向一次)。
对于相似性过滤做法:主要动机是观测几乎不变时没必要反复调用服务器 → 降低抖动与无效请求。具体做法(论文)是用关节空间距离作为近似(例如欧式距离),若两次观测间距离 <\varepsilon(阈值,\varepsilon\in\mathbb{R}^+)则丢弃本次请求。兜底做法是若队列真的耗尽,则无论相似度如何都要处理最近的观测,以防停摆。
重叠拼接(Overlap & Merge):核心思想通过重叠区域平滑过渡避免硬切抖动,数学上实现是设旧队列尾部与新队列头部重叠 w 步,对第 k=0,\dots,w-1 步做线性渐入融合:
a_{t+k}^{\text{merge}} = \alpha_k \tilde{a}_{t+1+k} + (1-\alpha_k) a_{t+k}, \quad
\alpha_k = \frac{k+1}{w}
也可用余弦窗、Slerp 或在位姿/速度层加滤波器;关键是重叠 + 平滑避免硬切抖动。
总结一下对于异步并发处理有优势,但是需要处理其中的细节主要是:
- 维护动作队列。前台执行当前队列,后台异步预测下一段;在重叠窗口内平滑拼接新旧段。
- 避免队列见底的解析下界,设控制周期为 \Delta t,则避免队列耗尽的充分条件为
g\ \ge\ \frac{\mathbb E[\ell_S]/\Delta t}{n}
其中 \ell_S 为一次(本地/远端)推理延迟,\Delta t 控制周期,n 为动作块长度。从触发到返回的时间内(平均 \mathbb{E}[\ell_S] 秒)你还要有足够的剩余动作可执行(约 \mathbb{E}[\ell_S]/\Delta t 个),所以触发点的剩余比例至少为这部分占 n 的比值。论文配合给出真实控制频率示例(如 30 FPS \to \Delta t=33,ms),并分析了不同 g 对队列曲线的影响(下图)。
数据
论文中提到的复现配置如下:
- 模型与输入:冻结 VLM,仅训动作专家;取 前半层 N=\lfloor L/2\rfloor 的 H^{(N)} → 投影成 O_N。图像 512×512;64 视觉 token/帧;状态→1 token;bfloat16。
- 动作块与解算: 每段 $n=50$;推理 10 步 Flow-Matching 积分。
- 优化:训练 200k step;global batch 256;AdamW(\beta_1=0.9,\ \beta_2=0.95);余弦退火学习率 1\times10^{-4}\to2.5\times10^{-6}。
- 参数量: 总计 ≈450M;动作专家 ≈100M;若 VLM 有 32 层,取前 16 层。
论文中提到需要关注的信息:
- 模拟(LIBERO/Meta-World):中等规模(~0.45B)已对标/超过若干更大基线;放大到 ~2.25B 继续提升。
- 真实机器人(SO100/101):多任务平均成功率 ≈78%,优于 π0 与 ACT。
- 异步 vs 同步:成功率相近,但异步平均完成时间缩短 ~30%,固定窗口内完成次数显著更多。
论文中提到的落地经验:
- 形状与缓存:把 H^{(N)}(T\times d_o) 投到 d_a 后当 K/V;两次 Cross 复用 KV 缓存。
- 因果掩码:Self-Attn 必须用因果掩码(第 i 步不可看未来)。
- 视觉压缩:优先用 space-to-depth 固定 64/帧;任务特别细腻时用 r=2(256 token)或多尺度/ROI 方案。
- 起步超参:n=50、积分步数 10、N=\lfloor L/2\rfloor、d_a=0.75d。
- 异步阈值:按 g\ge\frac{\ell_S/\Delta t}{n} 设定,取略高于下界更稳;配合相似度过滤与重叠拼接。
- 动作归一化:对不同量纲(角/位移/速度)做标准化,训练更稳、积分不发散。
- 交替注意力有效:Cross + 因果 Self 明显优于单一注意力;“用前半层”普遍优于“直接换小 VLM”。