机器人控制利器：MPC入门与实践解析

背景

MPC（Model Predictive Control）模型预测控制，是一种控制方法，广泛应用在机器人、无人驾驶、过程控制、能源系统等领域。它的核心思想用一句话来总结：利用系统模型预测未来，并通过优化选择当前最优的控制输入。

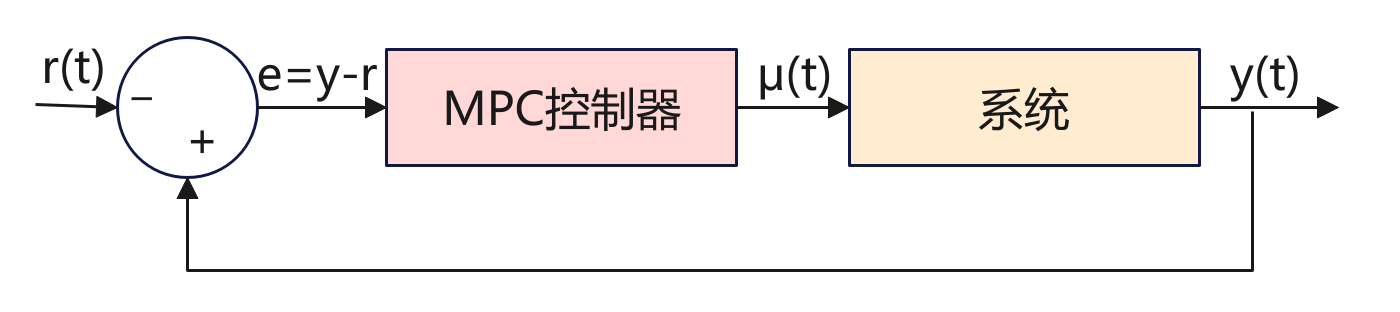
如上图是一个MPC应用框图，先来看看框图中的各个变量。

• r(t)：参考输入，系统希望达到的目标（设定值/reference signal），例如机器人要达到的位置、温度控制的目标值、车辆期望的速度等等。
• e：误差e(t) = y(t) – r(t)，用来计算实际的输出期望值的差距。
• μ(t)：控制输入，由MPC控制器计算出来，施加在系统上的控制量。
• y(t)：系统实际输出，比如位置、速度、温度等。

系统的目标是由MPC控制器计算输出一个μ(t)控制量，然后作用到系统，让系统的输出能够达到期望值。其中有一个反馈回路，形成一个闭环系统，实际的输出y(t)会反馈给比较器，与目标值对比，当未达到目标时，系统自动修正直到达到目标。

原理

系统模型

为了简单，我们先令系统的实际输出y=x，下面用数学建模来描述系统状态模型是

x_{k+1} = A x_k + B u_k

• $x_k$：系统在时刻$k$的状态，比如汽车的位置和速度[p,v]。
• $u_k$：系统在时刻$k$的控制输入，比如油门大小、方向盘角度、电机电压等。
• A：状态的转移矩阵，决定了系统状态的演化方式。
• B：输入矩阵，描述了控制输入如何影响状态的变换。
• $x_{k+1}$：系统在下一时刻$k+1$的状态。

A和B是两个矩阵，A决定系统 在没有控制输入时，状态如何随时间演化。B决定控制输入u_k如何影响的状态。

预测未来

MPC原理就是从当前状态x+k出发，用模型递推，预测出未来的N步（如果看过之前关于ACT原理，其实MPC有很多类似之处）：

x_{k+1},x_{k+2},x_{k+3},……,x_{k+N}

目标函数

工程中我们最主要的目标是要求出控制量u_t以便让系统最终调整到我们预期的状态。 那如何来设计这个系统了？ 前面我们建模了k时刻的状态x_t，那么这个状态+动作需要满足什么样的数学关系了？

与深度学习类似，我们要对状态+动作的数学关系求一个最小值的表达式。看公式：

J = \sum_{i=0}^{N-1} \Big[ (x_{k+i} – x_{k+i}^{\text{ref}})^T Q (x_{k+i} – x_{k+i}^{\text{ref}}) + u_{k+i}^T R u_{k+i} \Big]

上面的公式可以分为两部分，前面部分代表的是k时刻输出状态与目标状态误差值，后面部分是控制的动作。也就是说我们最核心的是要误差越小越好，同时控制的动作不要太大。误差小好理解，动作变化不要太大是因为要保证控制动作要平滑。两部分都是求平方e^2和u^2放大比例（跟深度学习中的损失差不多），同时各自有一个权重Q和R，这两个参数是权重参数可调，Q用来平衡快速到目标，R用来调节平衡动作要平稳。

公式中x和J可以说是已知的，那么就可以求出u控制量了。

约束条件

约束条件是在求解代价函数最小值过程中，显示的对控制量u、x_k做约束。这样的目的是比如对于车来说油门不能超过100%，速度不能超速，机械臂必能超过关节限位等。

因此在求救J时，可以添加约束条件，如下：

u_{\min} \leq u_k \leq u_{\max};x_{\min} \leq x_k \leq x_{\max}

第一个是 控制输入约束（油门、方向盘角度不能无限大）。第二个是 状态约束（位置、速度等不能超过物理限制）。

工作流程

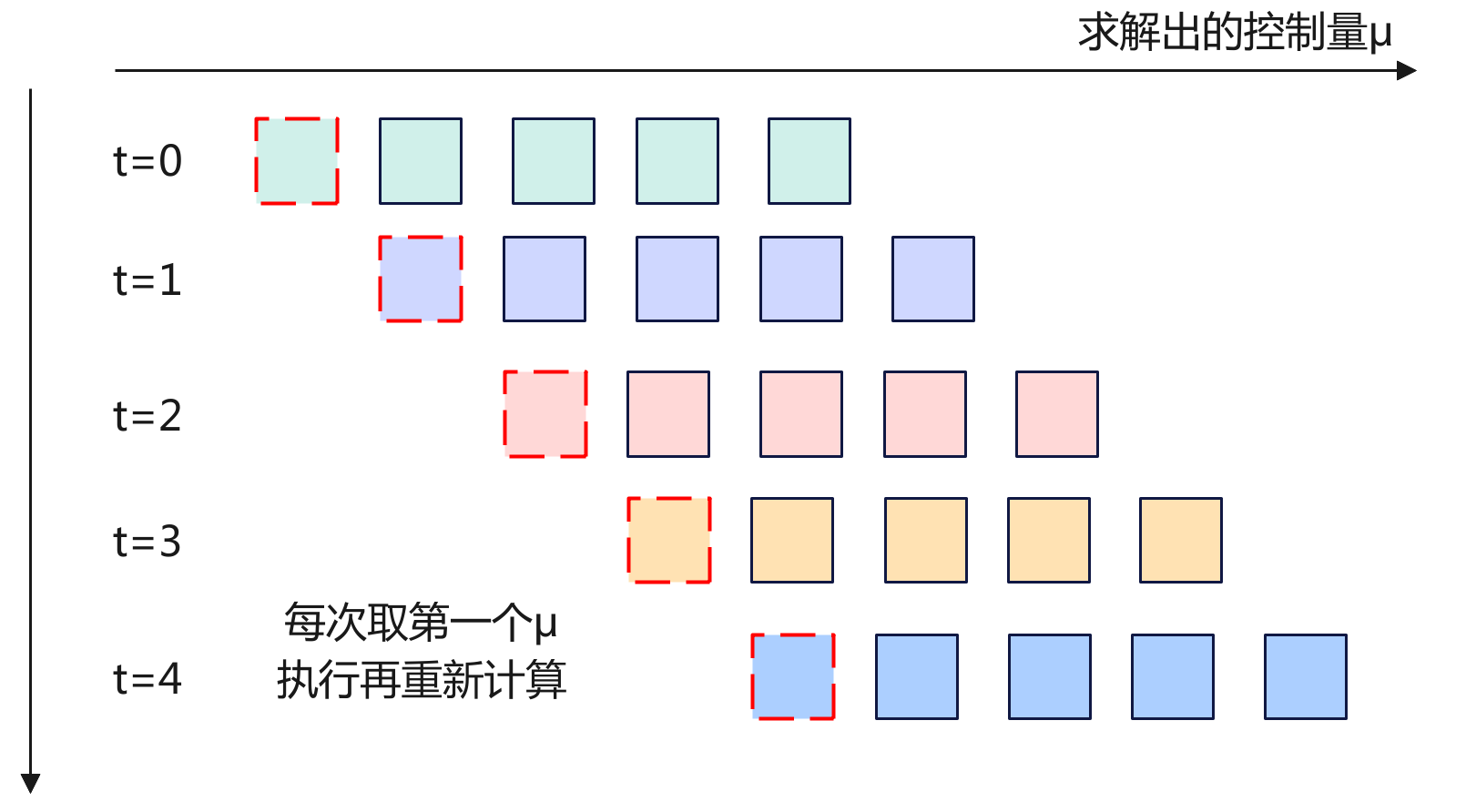
MPC控制系统中，其工作流程最核心的滚动时域控制，其核心点是每次预测出N步，但是并不是一下就全部执行完N步，因为预测也是有偏差同时在执行过程中会有变化。而是每次预测N步，但是只取第一步进行执行，然后根据新的输出结果重新预测下一个N步。这个其实跟ACT的时间集成有点类似，也就是在每个时间刻都会预测N步，而MPC是取第一步执行，而ACT是取k时刻和此前时刻的加权平均。

下面来看看具体的执行流程：

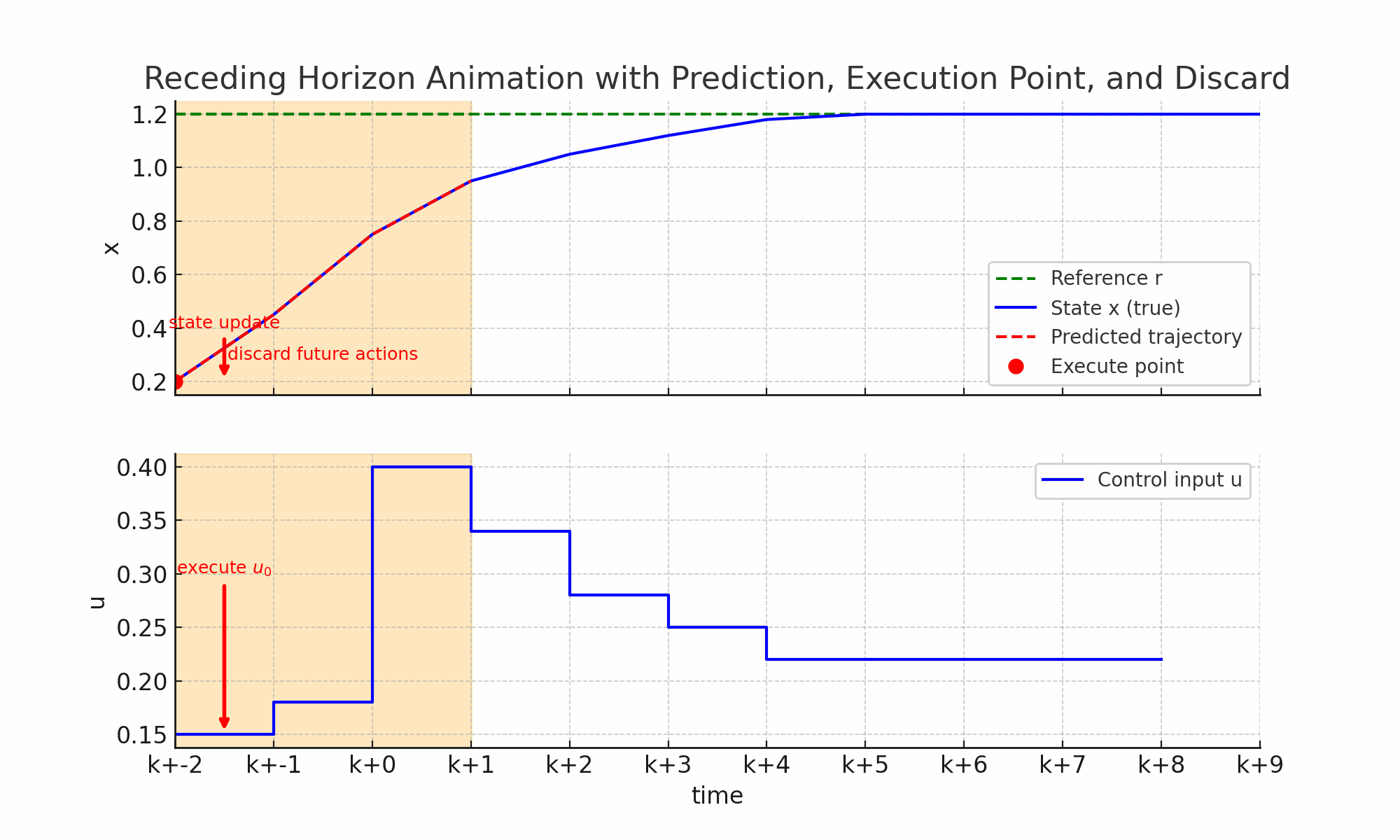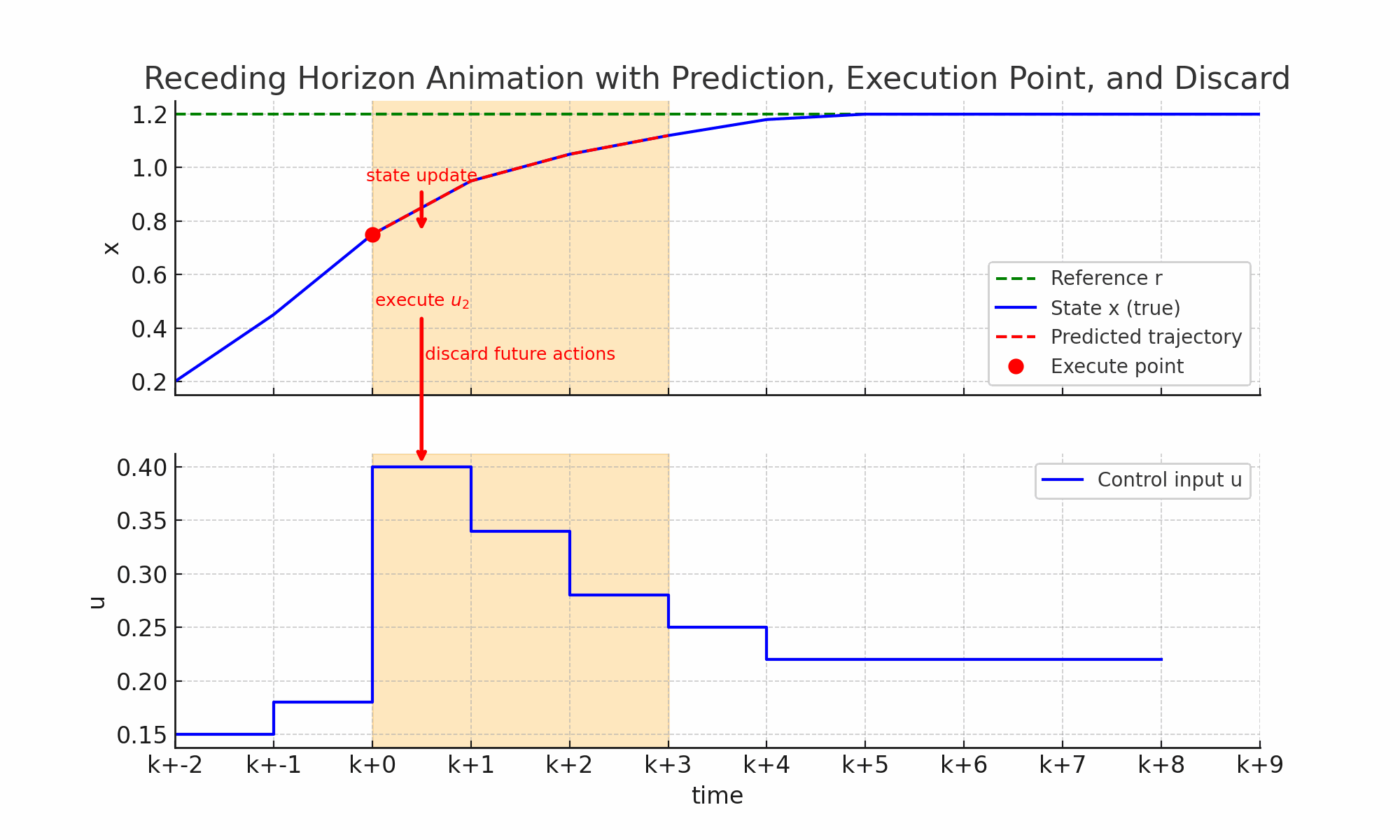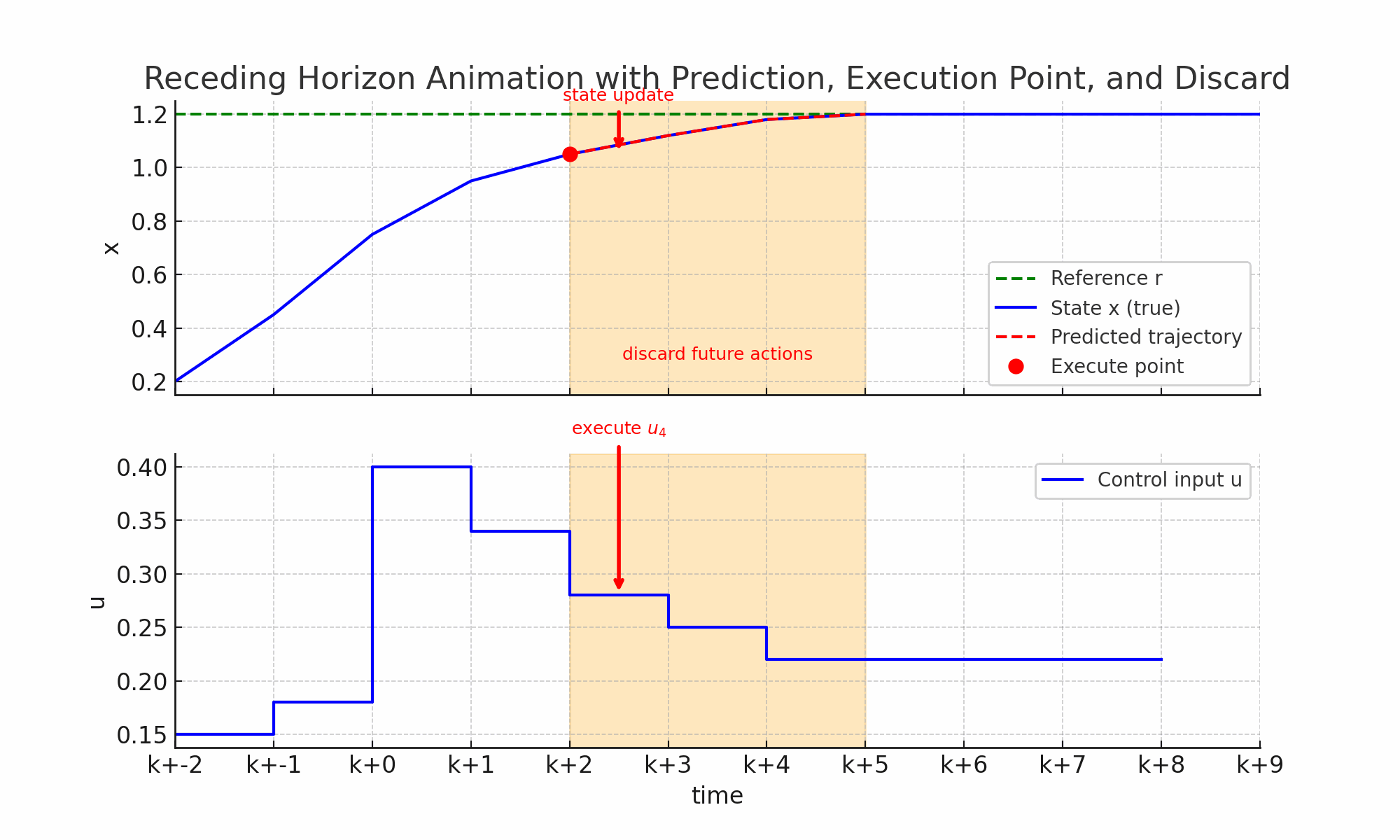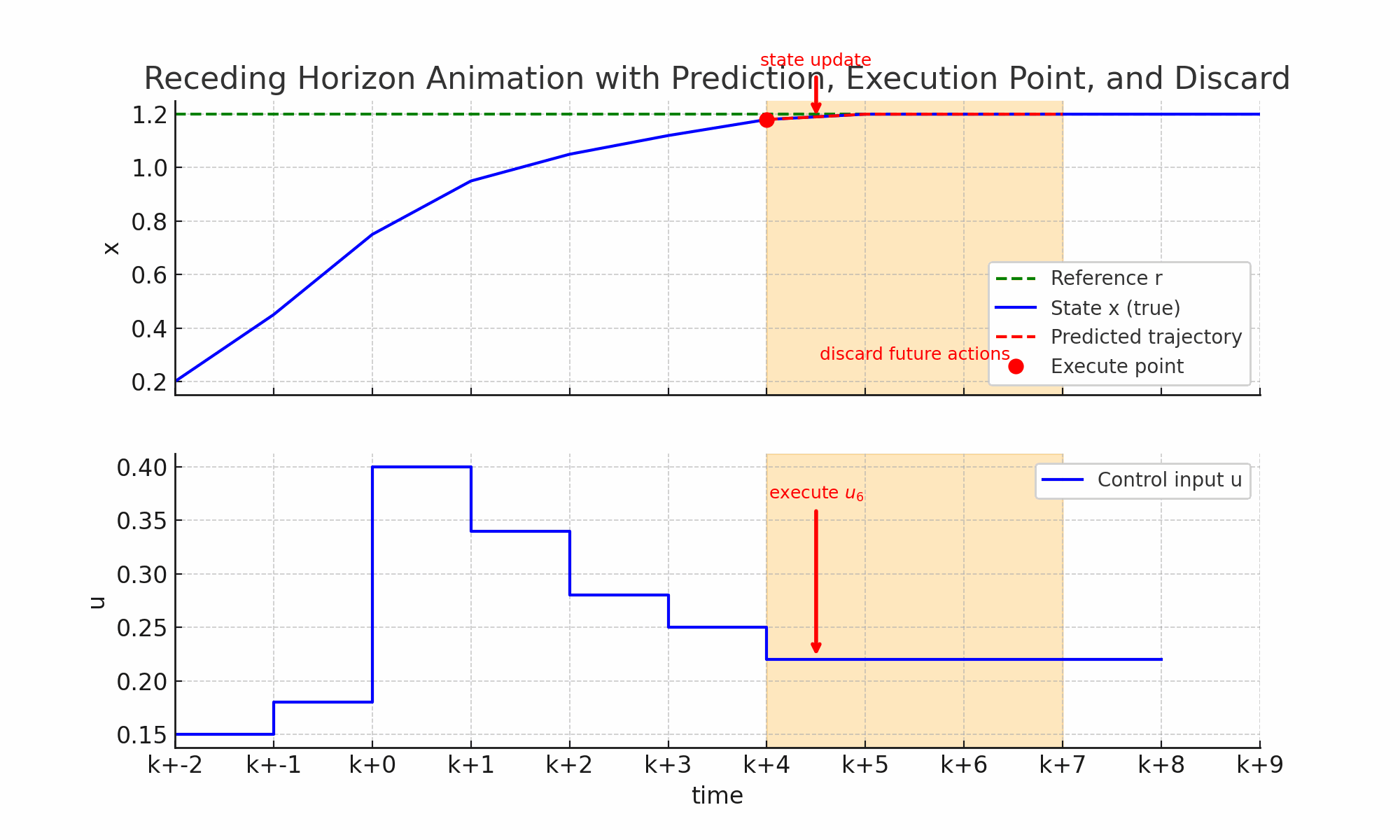
• 当前时刻K：系统处于某个状态如蓝线上面的红点，控制器采集到当前状态作为优化的起点。
• 预测未来N步：橙色窗口覆盖未来N步的时间区；红色虚线显示预测的未来轨迹，如果采用这一串控制动作U=[u_k,u_{k+1}…]系统怎么走。
• 优化并得到最优控制序列：在预测窗口里，MPC通过解J（误差+控制代价）最小值得到结果一整串最优控制动作序列U。
• 只执行一步：红色箭头指向当前窗口里的第一个控制输入u_k，下方蓝色阶梯控制曲线更新，系统真是状态推进到下一个时刻；上方状态曲线的红点更新到新的位置。
• 丢弃其余动作：窗口里的控制动作(u_{k+1},u_{k+2}…)丢弃，因为下一时刻会重新优化得到新的控制动作。
• 窗口前移，重复循环：橙色预测窗口右移一格(k->k+1->k+2)，控制器基于新状态重新预测、重新优化，再次执行第一步，丢弃其余周而复始直到达到目标。

因此整个过程核心就是MPC的滚动时域机制：预测未来——>优化整串动作——>执行第一步——>丢弃其余——>窗口前移——>重新计算。

示例程序

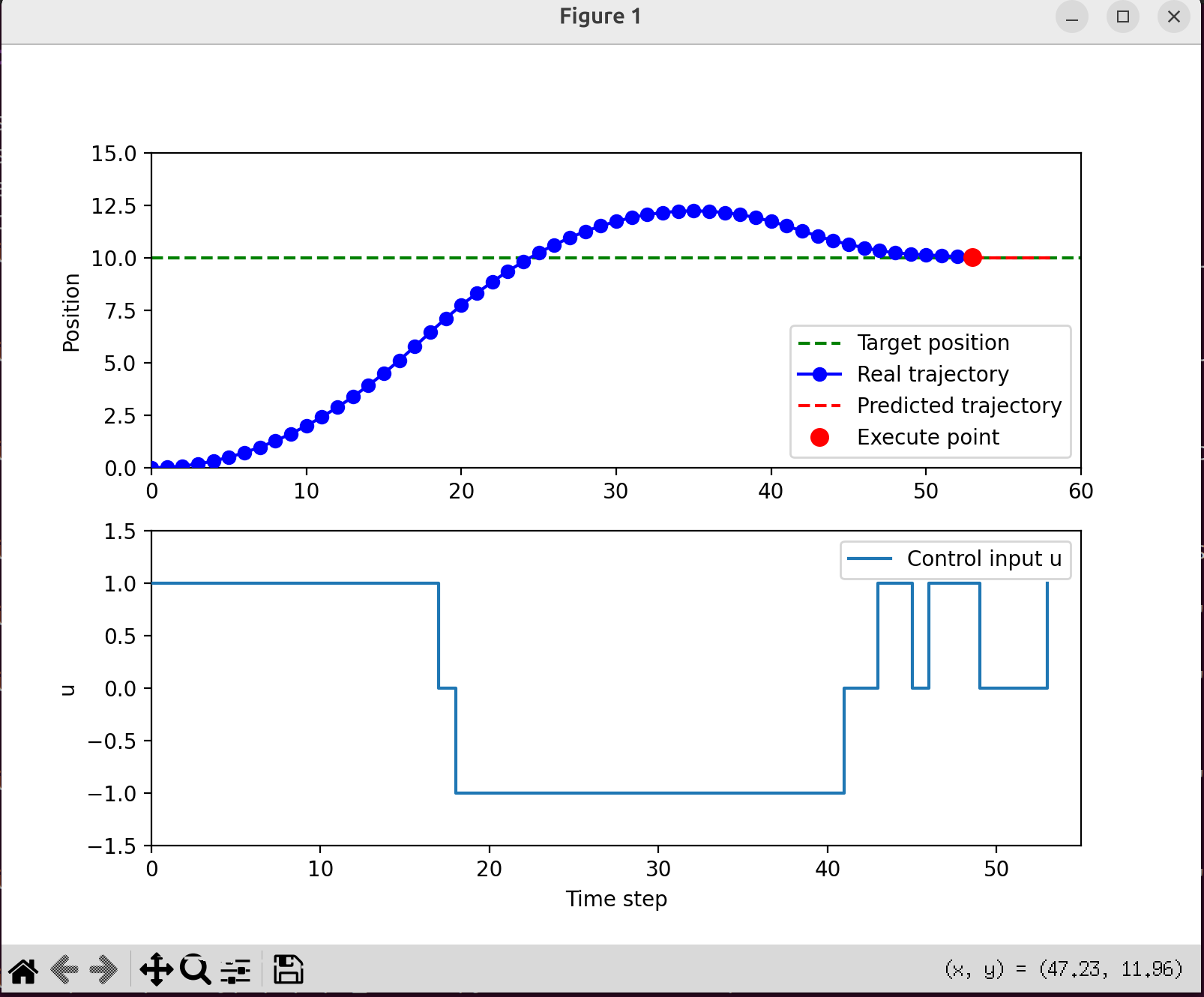
下面是一个简单的示例加深对MPC的认识。场景是一个一维的小车：

• 状态x=[位置，速度]，控制输入u=加速度。
• 小车从0开始，目标位置在10米，并希望最后速度接近0.
• 用MPC做控制，预测N步，计算代价，找到最优控制序列，但只执行第一个动作然后滚动。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

# --- 系统模型 (离散时间) ---
dt = 0.2
# 状态空间模型: x_{k+1} = A x_k + B u_k
# x = [位置, 速度]，u = 加速度
A = np.array([[1, dt],
              [0, 1]])
B = np.array([[0.5*dt**2],
              [dt]])

# 初始状态: 位置=0, 速度=0
x = np.array([0.0, 0.0])
# 目标状态: 位置=10, 速度=0 (停在10米处)
target = np.array([10.0, 0.0])

# --- MPC 参数 ---
N = 5                        # 预测时域长度 (未来看5步)
U_candidates = [-1, 0, 1]    # 控制输入候选集合 (加速度: -1=刹车, 0=不动, 1=加速)

def simulate(x0, u_seq):
    """
    给定初始状态 x0 和一段控制序列 u_seq，
    用系统模型递推未来轨迹，并计算代价 J
    """
    x = x0.copy()
    cost = 0.0
    traj = [x.copy()]  # 保存预测轨迹 (用于可视化)
    for u in u_seq:
        # 状态更新 (预测未来)
        x = A @ x + B.flatten()*u
        traj.append(x.copy())
        # 代价函数 J = 误差项 + 控制代价
        err = x - target
        cost += err[0]**2 + 0.3*err[1]**2 + 0.1*(u**2)
        # 位置误差^2 + 速度误差^2(权重0.3) + 控制输入^2(权重0.1)
    return cost, np.array(traj)

# --- MPC 主循环 (滚动时域控制) ---
history_x = []     # 真实执行的状态轨迹
history_u = []     # 实际执行的控制输入 (只取最优序列的第一步)
pred_trajs = []    # 每次优化得到的预测轨迹 (整串)

for step in range(60):
    best_cost = 1e9
    best_seq = None
    best_traj = None

    # 穷举所有可能的控制序列 U = [u_k, u_{k+1}, ..., u_{k+N-1}]
    for U in np.array(np.meshgrid(*[U_candidates]*N)).T.reshape(-1,N):
        cost, traj = simulate(x, U)
        if cost < best_cost:
            best_cost = cost
            best_seq = U      # 当前最优控制序列
            best_traj = traj  # 当前最优预测轨迹

    # 保存数据 (真实轨迹、控制输入、预测轨迹)
    history_x.append(x.copy())
    history_u.append(best_seq[0])  # 只执行第一步 u_k*
    pred_trajs.append(best_traj)   # 保存整条预测轨迹用于画红虚线

    # 执行第一步 (滚动时域控制的核心：只执行u_k)
    u = best_seq[0]
    x = A @ x + B.flatten()*u

    # 收敛条件 (位置接近10, 速度≈0)
    if abs(x[0]-target[0]) < 0.1 and abs(x[1]-target[1]) < 0.1:
        history_x.append(x.copy())
        history_u.append(0)   # 终端时控制输入设为0
        break

history_x = np.array(history_x)

# --- 动态可视化 ---
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(8, 6))

# 上图：位置随时间
ax1.axhline(target[0], color="green", linestyle="--", label="Target position")
(line_real,) = ax1.plot([], [], "bo-", label="Real trajectory")   # 蓝点=真实轨迹
(line_pred,) = ax1.plot([], [], "r--", label="Predicted trajectory")  # 红虚线=预测轨迹
(point_exec,) = ax1.plot([], [], "ro", markersize=8, label="Execute point") # 红点=执行点
ax1.set_xlim(0, len(history_x)+N)
ax1.set_ylim(0, target[0]+5)
ax1.set_ylabel("Position")
ax1.legend()

# 下图：控制输入
(line_u,) = ax2.step([], [], where="post", label="Control input u")
ax2.set_xlim(0, len(history_u))
ax2.set_ylim(min(U_candidates)-0.5, max(U_candidates)+0.5)
ax2.set_xlabel("Time step")
ax2.set_ylabel("u")
ax2.legend()

# --- 动画更新函数 ---
def update(frame):
    # 蓝线：实际轨迹
    line_real.set_data(np.arange(frame+1), history_x[:frame+1,0])
    # 红虚线：预测轨迹 (窗口内)
    pred = pred_trajs[frame]
    line_pred.set_data(np.arange(frame, frame+len(pred)), pred[:,0])
    # 红点：当前执行点
    point_exec.set_data([frame], [history_x[frame,0]])
    # 阶梯：控制输入
    line_u.set_data(np.arange(frame+1), history_u[:frame+1])
    return line_real, line_pred, point_exec, line_u

# 动画循环：frames=len(pred_trajs)，表示每个MPC优化时刻
ani = animation.FuncAnimation(fig, update, frames=len(pred_trajs),
                              interval=800, blit=True, repeat=False)

plt.show()