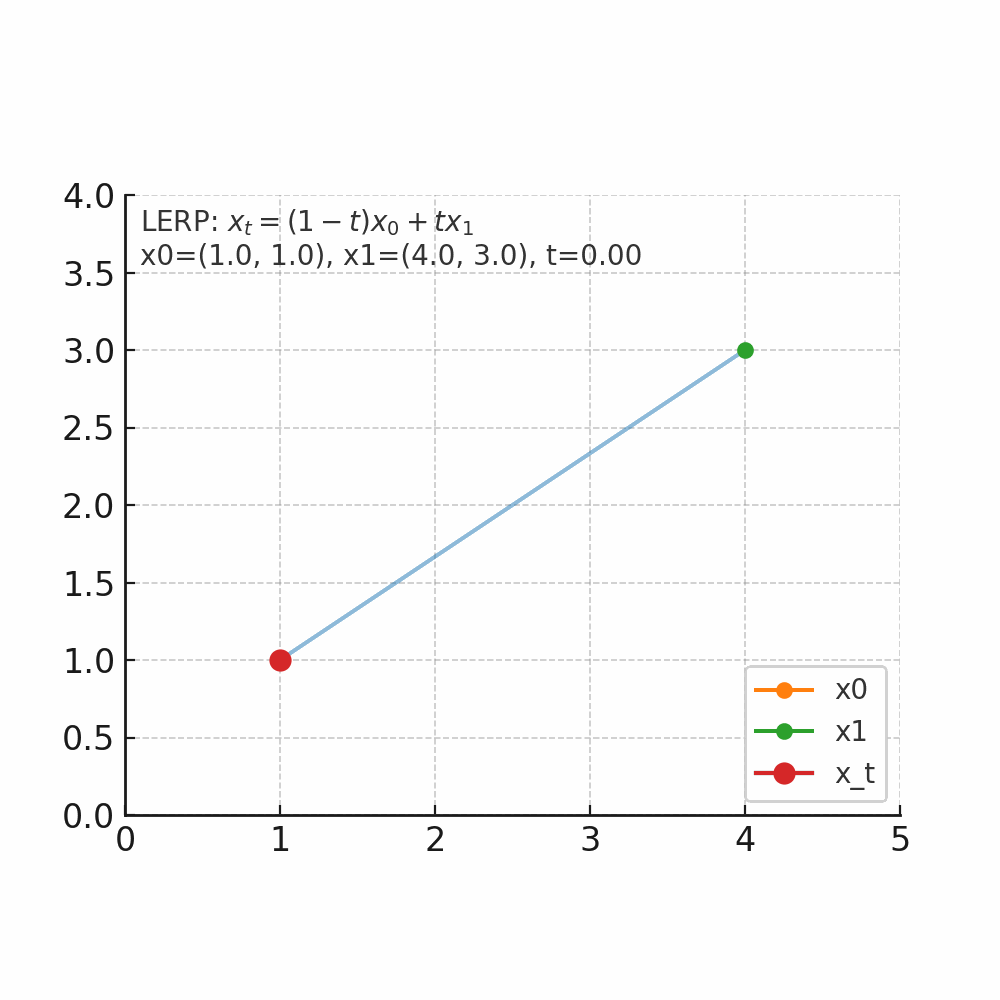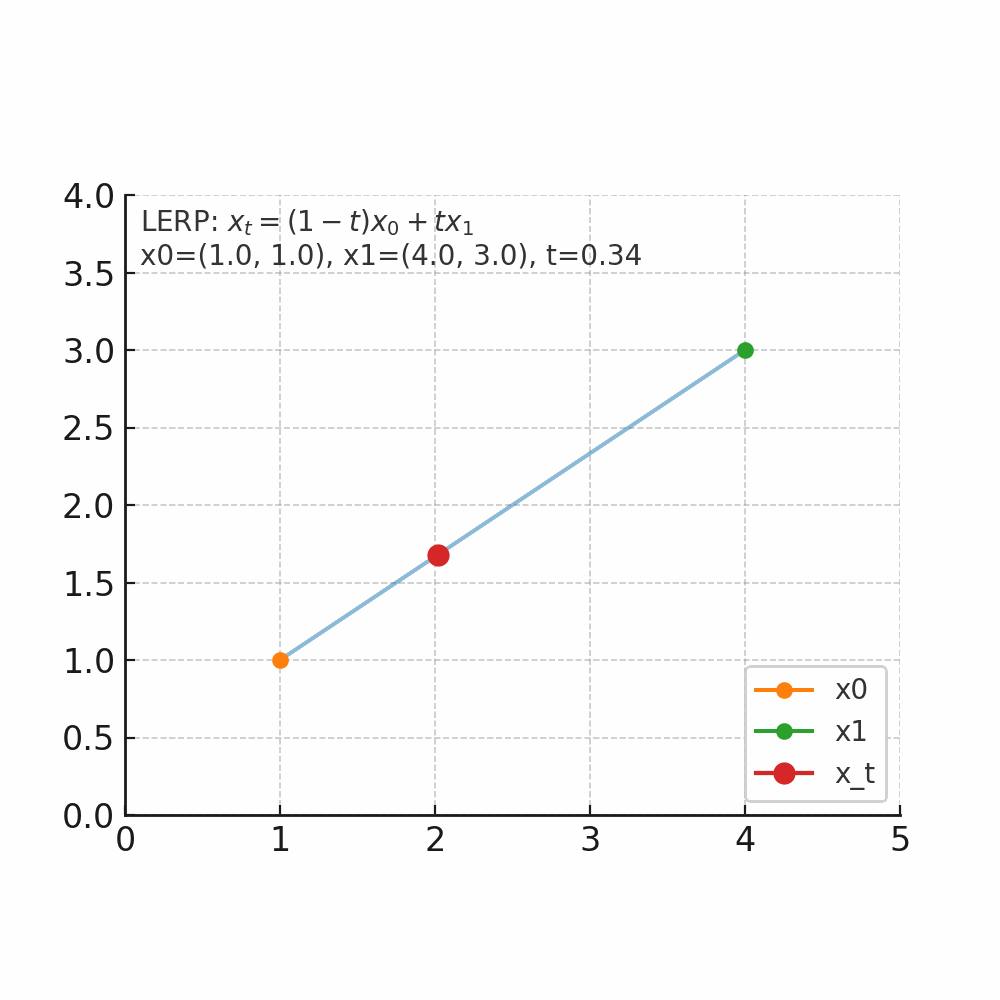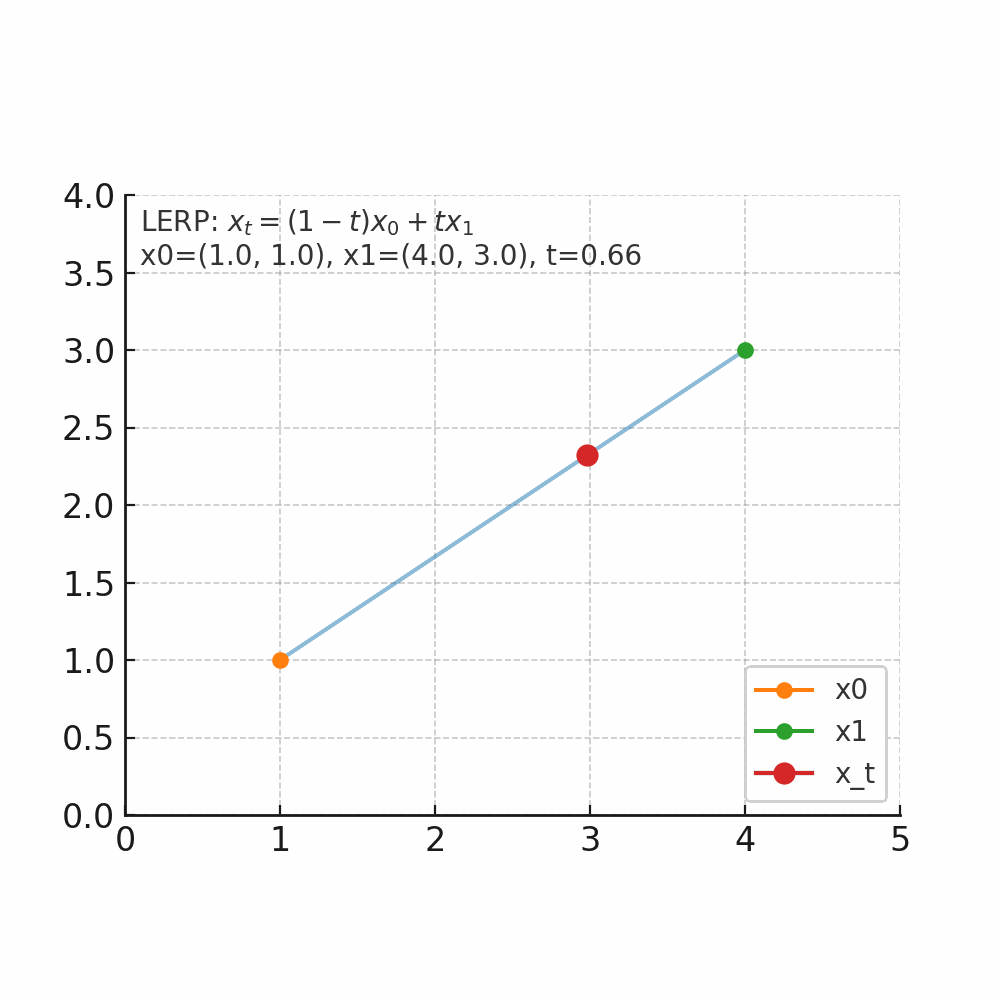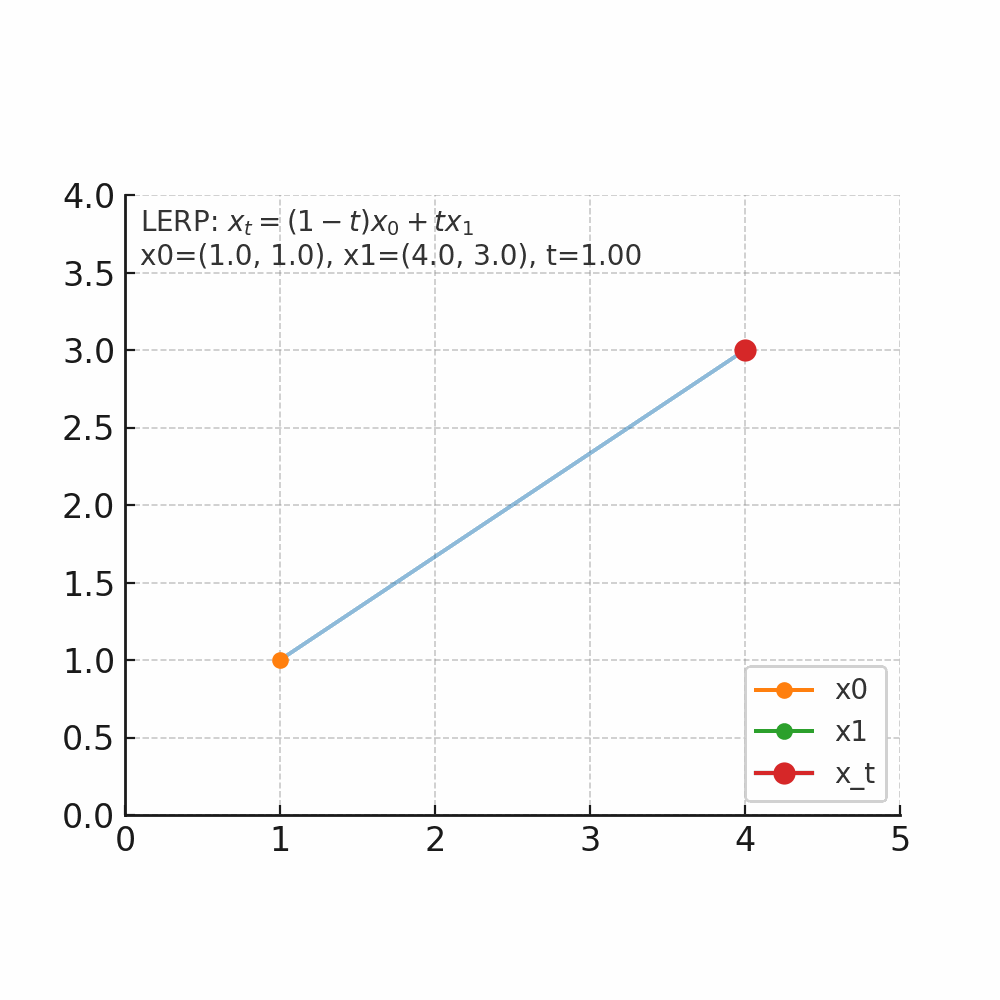
什么是插值 插值的核心问题是：在已知两个点的情况下，如何找到它们之间的中间点。 举个人走路的例子，起点在家门口(A点)，终点在公司(B点)，总的路程为1000米，假设人是匀速移动，如果走到一半(t=0.5)，那么人就在家和公司的正中间，如果走到四分之一(t=0.25)，那么离家250米，离公司750米。 线性插值（LERP） 是最简单的一种：它假设两个点之间的变化是“直线型、匀速”的。 公式 $$ x_t = (1-t)x_0 + t x_1, \quad t \in [0,1] $$ 把两个量$x_0$和$x_1$按加权$1-t$与$t$做加权平均，得到他们之间的线性过渡点。$x_0$是起点，$x_1$是终点，$t$是插值因子，控制起点与重点的位置。当 $t=0$，结果是 $x_0$；当 $t=1$，结果是 $x_1$；当 $t=0.5$，结果是中点；$t$从0到1连续变化时，$x_t$沿着二者之间等速变化（为什么是等速，待会解释）。 先上个图看看直观体会一下。 如图所示起点$x_0$为坐标（1，1），终点$x_1$（4，3），当$t$从0开始连续变化是，$x_t$的位置会朝着$x_1$的方向变化。 当$t=0$时，坐标为(1 - 0) x (1, 1) + 0 x (4, 3) = (1, 1)。 当$t=0.2$时，坐标为(1 - 0.2) x (1, 1) + 0.2 x (4, 3) = (1.6, 1.4)。 当$t=0.5$时，坐标为(1 - 0.5) x (1, 1) + 0.5 x (4, 3) = (2.5, 2)。 当$t=1$时，坐标为(1 - 01) x (1, 1) + 1 x (4, 3) = (4, 3)。 通过公式可以算出每个时间的位置，但是如果要知道每个位置变化的速度/趋势我们应该怎么来衡量了？ 那自然就是要求导数了。 $$ \frac{d}{dt}x_t = x_1 - x_0 $$ 可以看到其倒数是一个常数，那就意味着变化是匀速的，以上图为例，都是朝着(4,3)-(1,1)=(3,2)的向量方向去变化。 有了这个变化量，假设我们时间步$\Delta t=0.1$，那么意味着每次变化的位置是0.1 x (3,2) = (0.3, 0.2)；假设当前位置是(1,1)那么就可以计算出下一个时间步的位置为$(1,1)+(0.3,0.2)=(1.3,0.2)$。这就与我们此前flow matching里面的公式$x_{k+1} = x_k + v_\theta(x_k, t_k)\Delta t$。

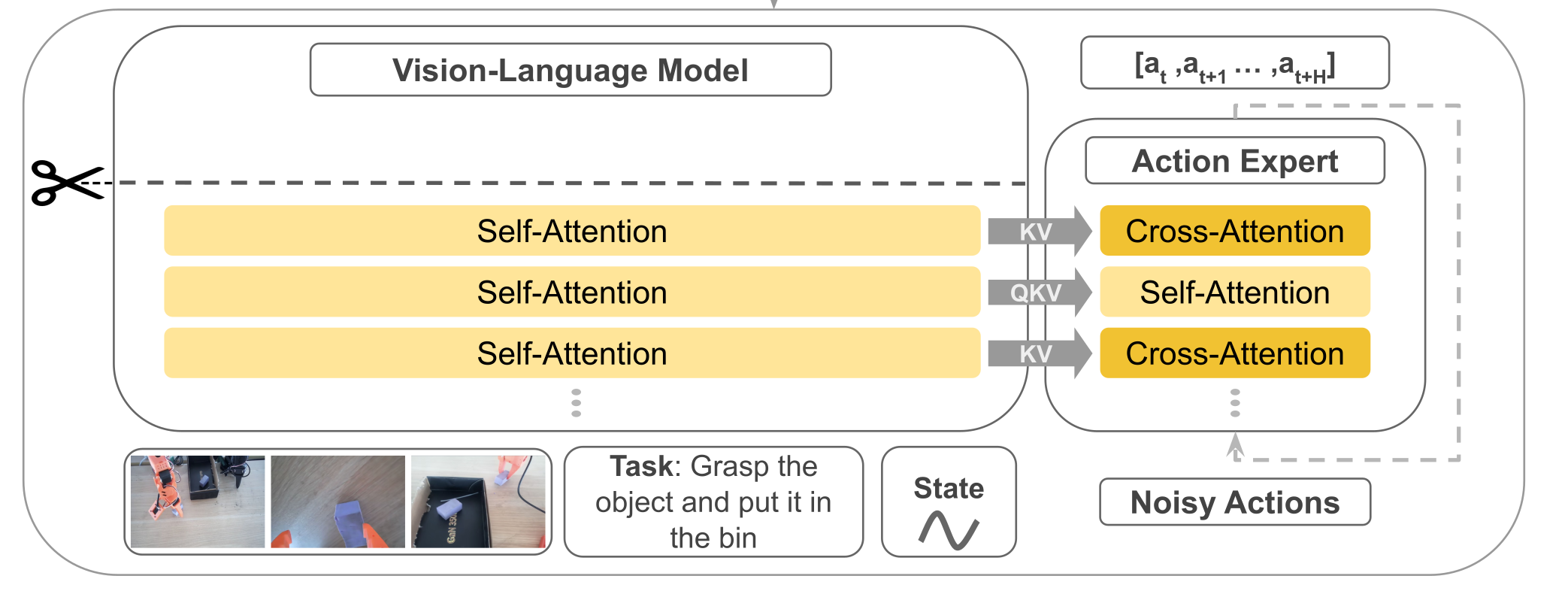
概述 SmolVLA 是一套轻量级视觉-语言-行动（VLA）策略：前端用小型 VLM（视觉 SigLIP + 语言 SmolLM2）做感知与理解；后端用一个“动作专家”专门预测一段连续的低层控制。它与Pi0相比，参数规模少了将近10倍只有约0.45B（450M）。它的目标是在低算力下也能稳定执行多任务机器人控制，并保持接近甚至超过更大模型的效果。 SmolVLA 通过冻结 VLM、只训练动作专家（Action Expert），再配上四件“硬核小技巧”——取 VLM 的前半层、把每帧视觉 token 压到 64、以及Self-Attn—>Cross-Attn交替方式、异步推理；在大幅降算力与时延的同时，保持/逼近甚至超过更大模型的性能；注意力计算交替方式让动作专家既能不断获取外部视觉/语言指导，又能在内部序列里建立自己的时序与物理一致性，从而在算力可控的前提下提升稳定性和表现；提供异步执行，把“算下一段动作”和“执行当前动作”并行起来，显著减少空窗时间。 原理 结构 其模型结构主要有前端的VLM+后端的动作专家Action Expert组成，结构组成与Pi基本一致但实现方式有很大差异不同。先总结一下组件，稍后我们在稍作展开补充。 输入：文本指令token+视觉token（多摄像头采集的图像）+机器的状态（关节角、传感器）。 VLM（感知端）：采用SmolVLM-2，VLM共有L层，但是只N=⌊L/2⌋层隐藏表示喂给动作专家。 Action Expert（控制端）：一个Flow Matching Transformer，以以Cross → Causal Self → Cross 的“三明治”层为基本单元，按块预测n步动作序列。 输出：一次预测长度为n的动作块，对应机器的控制指令。 SmolVLA与Pi0有很多相似之处，不过其背后有四个关键设计，分别是Layer Skipping（层跳过）、Visual tokens reduction（视觉token压缩）、动作专家交替Self-Attn与Cross-Attn、异步推理。本小节先围绕前面3部分进行解析，异步推理于后续章节展开。 （1）Layer Skipping 层跳过就是把感知端的VLM（视觉+语言）的解码器中间层拿来当条件特征，而不是等它把整个层都计算完再输出；具体的做法就是只去$N=L/2$层的隐藏层表示送给动作专家，VLM权重冻结不训练。之所以要这样做经验规律表示（论文中作者提到）深层 LLM 层更偏“词级生成/长链路语义”，而中层已经集中了“指令 + 视觉”的对齐语义，对控制足够；继续往后让语言头生成 token 既耗算，又不是控制必须。前半层就停下，少算一半的自注意 + MLP，显存开销也随之下降。 大概得实现是把“文本指令 token、图像 token、状态 token”拼接，送入解码器；在第$N$层获取特征信息H然后用一个线性投影到Action expert所需的维度$d_a$作为$K/V$。如果在长时、极强推理型任务（需要深层语言生成）时可以适当调大N。 （2）视觉token压缩 在transformer里面，“token”就是序列里的一个位置。对图像来说，我们把一张图拆成很多小块（patch）或网格上的特征点，每个块/点用一个向量表示，这个向量就是视觉 token（不明白的可以看看ViT原理解析介绍）。视觉token压缩具体的做法是保整图、不裁块，把空间上密的token折叠到通道里，从而让token数变少。 设 ViT patch 后得到的特征图大小为 $\frac{H}{p} \times \frac{W}{p} \times d$，选一个下采样因子 $r$ (整数)，做 space-to-depth： $$ \underbrace{\frac{H}{p} \times \frac{W}{p}}{\text{原网格}} \xrightarrow{\div r} \underbrace{\frac{H}{pr} \times \frac{W}{pr}}{\text{更稀疏的网格}}, \quad \underbrace{d}{\text{通道}} \xrightarrow{\times r^2} \underbrace{d \cdot r^2}{\text{更厚的通道}} $$ 计算示例： 输入尺寸：$512 \times 512$ 图像 Patch大小 $p=16$ ⇒ $32 \times 32$ token网格 选$r=4$ ⇒ $\frac{32}{4} \times \frac{32}{4} = 8 \times 8$ 网格 Token数：$8 \times 8 = 64$（减少$4^2=16$倍） 通道维度：$d=3 \rightarrow d=3 \times 16=48$ 可以看到如果是按照ViT的默认方式patch数量为32x32=1024，每个patch的维度为3x16x16=768，然后如果输入编码的$d_mode=512$那么经过线性投影变成矩阵(1024,512)，即1024个token数量，每个token维度是512；而如果进行压缩后patch数量为8x8=64，每个patch的维度为48x16x16=12288，经过线性投影后变成(64,512)即64个token，每个维度是512。这里也可以看到原来是768降为到512，压缩的是从12288降维到512，降得比较猛，效果真的没有衰减吗？ 总结一下smolvla在视觉token上进行了压缩，使用space-to-depth，对于512X512的图每帧token从1024降低到了64帧，如ViT的patch操作后得到的特征图维度为$\mathbb{R}^{\frac{H}{p} \times \frac{W}{p} \times d}$，选择下采样因子 $r$（整数）进行space-to-depth操作： $$ \mathbb{R}^{\frac{H}{p}\times\frac{W}{p}\times d} \xrightarrow{\text{S2D}_{r}} \mathbb{R}^{\frac{H}{pr}\times\frac{W}{pr}\times(d\cdot r^{2})} $$ 这样token数减少$r^{2}$倍，把细节挪到通道数去。 （3）动作专家交替Self-Attn与Cross-Attn 在动作专家中使用了交叉注意力机制，具体的排布可以配置。VLM的每一层与右边的Expert是一一对齐的，当然也可以配置Expert模型只有VLM层数的一半，每两层VLM才有一层Expert，那么其中VLM对齐层将为NONE，下图以VLM和Expert都为4层来示例交替注意力的实现。 Self-Attn（管自己，守时序）：只允许第 i 步看 ≤i 的历史步（因果掩码），在动作序列内部传播动力学与约束，做轨迹的时间一致性与平滑。这一步相当于“内化刚才读到的证据”并让各步动作彼此协调。在计算注意力时，会将VLM的QKV与Expert的QKV进行拼接起来一起送入transformer计算，但通过掩码保证 VLM 的Q只看自己（不去读 Expert），而 Expert 的 Q 可以访问 VLM 的 K/V（即“读”VLM 语义），这样既提供了计算效率也提升了Expert的语义丰富性。 Cross-Attn（看环境，取证）：看环境取证，让每个动作 token 先从条件特征里“读”一遍（条件=VLM中间层输出，含文本指令+多路视觉+状态）。这样动作表示一开始就被场景锚定，知道当下该关注哪里/哪件物体。具体是交叉注意力计算Q来自Expert Action自己，而K/V 来自 VLM 对应层的输出缓存。 训练 目标让动作专家 在观测条件 $o_t$ 下输出$v_\theta$速度场，把“噪声动作”沿路径推向真实动作块 $A_t$。这里跟Pi0和Flow Matching是一样大同小异，就简要说明一下。 观测条件：$o_t=H^{(N)}\in\mathbb{R}^{T\times d_o}\ \xrightarrow{\text{proj}}\ O_N\in\mathbb{R}^{T\times d_a}$（VLM 冻结；$O_N$ 作为 Cross-Attn 的 K/V）。 真实动作块：$A_t\in\mathbb{R}^{n\times d_{\text{act}}}$（建议标准化/白化）。 噪声：$\varepsilon\sim\mathcal N(0,I)$（同形）。 路径时间：$\tau\sim\mathrm{Beta}(\alpha,\beta)$。这里与Pi0不同。 路径与目标速度场： $$ A_t^{\tau}=\tau A_t+(1-\tau)\varepsilon,\left(A_t^{\tau}\mid A_t\right)=\varepsilon-A_t $$ 计算损失函数： $$ \mathcal{L}^{\tau}(\theta) = \mathbb{E}{p\left(\mathbf{A}{t} \mid \mathbf{o}{t}\right), q\left(\mathbf{A}{t}^{\tau} \mid \mathbf{A}{t}\right)} \left[ \left|| \mathbf{v}{\theta}\left(\mathbf{A}{t}^{\tau}, \mathbf{o}{t}\right) - \mathbf{u}\left(\mathbf{A}{t}^{\tau} \mid \mathbf{A}{t}\right) \right||^{2} \right] $$ 这里 $||\cdot||^{2}$ 表示欧氏范数平方；实现即逐元素 MSE。 为提升推理效率，动作专家隐藏宽度取 $d_a=0.75\times d$（$d$ 为 VLM 的隐藏宽度）。 以下是一个简单的示例，可看看过程理解一下。 # 条件：取 VLM 第 N 层隐藏（冻结） with torch.no_grad(): H = vlm_hidden_at_layer_N(obs_tokens) # [T, d_o] KV = proj(H) # [T, d_a] 供 Cross-Attn 作 K/V（可缓存） # 构造路径与目标速度 A = sample_action_chunk() # [n, d_act] (已标准化) eps = torch.randn_like(A) # [n, d_act] tau = Beta(alpha, beta).sample(()).to(A.device) A_tau = tau * A + (1 - tau) * eps u = eps - A # 前向与损失 pred = v_theta(A_tau, KV) # 与 u 同形 loss = F.mse_loss(pred, u) # 对应 ||·||^2 loss.backward(); optimizer.step(); optimizer.zero_grad() 推理 在SmolVLA提到了异步推理，先来看看同步推理。 取最新观测 → 得到 $O_N$； 以噪声初始化，做 $K\approx10$ 步显式积分（Euler/Heun）得到一个动作块 $[a_t,\dots,a_{t+n-1}]$； 执行动作块 → 重复。 同步（sync）推理一次性生成长度为 $n$ 的动作队列（chunk）$A_t=\big[a_t,\dots,a_{t+n-1}\big]$，执行完再用新观测预测下一段。执行与推理串行，会产生“空窗”（执行停下等待推理）。而异步（async）推理是解耦“动作执行”和“动作预测”。机器人端持续消费现有队列；当队列余额低于阈值就异步把当前观测发给策略端预测“下一段”，回来后与旧队列重叠拼接。这样执行与推理并行，显著降低总时延，同时仍保持接近的成功率。 异步推理在架构上可以分为两个部分： RobotClient（机器人端）：以控制周期 $\Delta t$ 持续下发队列头部动作；本地维护动作队列 $A_t$ 与触发逻辑；可做相似度过滤（见下节）。 PolicyServer（策略端）：接收观测 $o_t$，运行策略 $\pi$ 预测新队列 $\tilde A_{t+1}$ 后返回；可放在更强的远端算力（GPU/工作站/云）。 看看论文中给出的算法实现： 设时域 $T$、段长 $n$、触发阈值 $g\in[0,1]$。 初始化：采集 $o_0$，发送到策略端，得到首段 $A_0\leftarrow\pi(o_0)$。 主循环 对 $t=0\dots T$：取出并执行一步 $a_t\leftarrow\text{PopFront}(A_t)$；若 队列余额占比 $\dfrac{|A_t|}{n}<g$，采集新观测 $o_{t+1}$；若 NeedsProcessing$(o_{t+1})$ 为真（见“相似度过滤”），则异步触发：①发送 $o_{t+1}$ 到策略端，得到新段 $\tilde A_{t+1}\leftarrow\pi(o_{t+1})$（异步返回）；②用重叠拼接函数 $f(\cdot)$ 合并：$A_{t+1}\leftarrow f(A_t,\tilde A_{t+1})$；若本轮异步推理尚未结束：$A_{t+1}\leftarrow A_t$（继续消费旧队列）。 论文中的 NeedsProcessing 用于避免重复观测触发；$f$ 表示对重叠步的拼接（线性渐入/平滑器等，见下重叠拼接（Overlap & Merge））。 关键触发量，队列余额阈值 $g$： 触发条件：当 $\dfrac{|A_t|}{n}<g$ 时触发一次异步预测。 直觉：$g$ 越大，越提前触发，越不容易见底；但也会更频繁地调用策略端（算力/网络开销更高）。 论文的三个代表场景：$g=0$（顺序极限）：耗尽队列才发起新预测 → 一定出现空窗等待；$g=0.7$（典型异步）：每段大约消耗 $1-g=0.3$ 的比例就触发，计算摊在执行过程中，队列不见底；$g=1$（计算密集极限）：步步都发观测 → 几乎“满队列”，反应最快但计算最贵（等同每个 tick 都前向一次）。 对于相似性过滤做法：主要动机是观测几乎不变时没必要反复调用服务器 → 降低抖动与无效请求。具体做法（论文）是用关节空间距离作为近似（例如欧式距离），若两次观测间距离 $<\varepsilon$（阈值，$\varepsilon\in\mathbb{R}^+$）则丢弃本次请求。兜底做法是若队列真的耗尽，则无论相似度如何都要处理最近的观测，以防停摆。 重叠拼接（Overlap & Merge）：核心思想通过重叠区域平滑过渡避免硬切抖动，数学上实现是设旧队列尾部与新队列头部重叠 $w$ 步，对第 $k=0,\dots,w-1$ 步做线性渐入融合： $$ a_{t+k}^{\text{merge}} = \alpha_k \tilde{a}{t+1+k} + (1-\alpha_k) a{t+k}, \quad \alpha_k = \frac{k+1}{w} $$ 也可用余弦窗、Slerp 或在位姿/速度层加滤波器；关键是重叠 + 平滑避免硬切抖动。 总结一下对于异步并发处理有优势，但是需要处理其中的细节主要是： 维护动作队列。前台执行当前队列，后台异步预测下一段；在重叠窗口内平滑拼接新旧段。 避免队列见底的解析下界，设控制周期为 $\Delta t$，则避免队列耗尽的充分条件为 $$ g\ \ge\ \frac{\mathbb E[\ell_S]/\Delta t}{n} $$ 其中 $\ell_S$ 为一次（本地/远端）推理延迟，$\Delta t$ 控制周期，$n$ 为动作块长度。从触发到返回的时间内（平均 $\mathbb{E}[\ell_S]$ 秒）你还要有足够的剩余动作可执行（约 $\mathbb{E}[\ell_S]/\Delta t$ 个），所以触发点的剩余比例至少为这部分占 $n$ 的比值。论文配合给出真实控制频率示例（如 $30$ FPS $\to \Delta t=33,$ms），并分析了不同 $g$ 对队列曲线的影响（下图）。 数据 论文中提到的复现配置如下： 模型与输入：冻结 VLM，仅训动作专家；取 前半层 $N=\lfloor L/2\rfloor$ 的 $H^{(N)}$ → 投影成 $O_N$。图像 512×512；64 视觉 token/帧；状态→1 token；bfloat16。 动作块与解算： 每段 $n=50$；推理 10 步 Flow-Matching 积分。 优化：训练 200k step；global batch 256；AdamW（$\beta_1=0.9,\ \beta_2=0.95$）；余弦退火学习率 $1\times10^{-4}\to2.5\times10^{-6}$。 参数量： 总计 ≈450M；动作专家 ≈100M；若 VLM 有 32 层，取前 16 层。 论文中提到需要关注的信息： 模拟（LIBERO/Meta-World）：中等规模（~0.45B）已对标/超过若干更大基线；放大到 ~2.25B 继续提升。 真实机器人（SO100/101）：多任务平均成功率 ≈78%，优于 π0 与 ACT。 异步 vs 同步：成功率相近，但异步平均完成时间缩短 ~30%，固定窗口内完成次数显著更多。 论文中提到的落地经验： 形状与缓存：把 $H^{(N)}(T\times d_o)$ 投到 $d_a$ 后当 K/V；两次 Cross 复用 KV 缓存。 因果掩码：Self-Attn 必须用因果掩码（第 $i$ 步不可看未来）。 视觉压缩：优先用 space-to-depth 固定 64/帧；任务特别细腻时用 $r=2$（256 token）或多尺度/ROI 方案。 起步超参：$n=50$、积分步数 10、$N=\lfloor L/2\rfloor$、$d_a=0.75d$。 异步阈值：按 $g\ge\frac{\ell_S/\Delta t}{n}$ 设定，取略高于下界更稳；配合相似度过滤与重叠拼接。 动作归一化：对不同量纲（角/位移/速度）做标准化，训练更稳、积分不发散。 交替注意力有效：Cross + 因果 Self 明显优于单一注意力；“用前半层”普遍优于“直接换小 VLM”。 参考：https://arxiv.org/abs/2506.01844

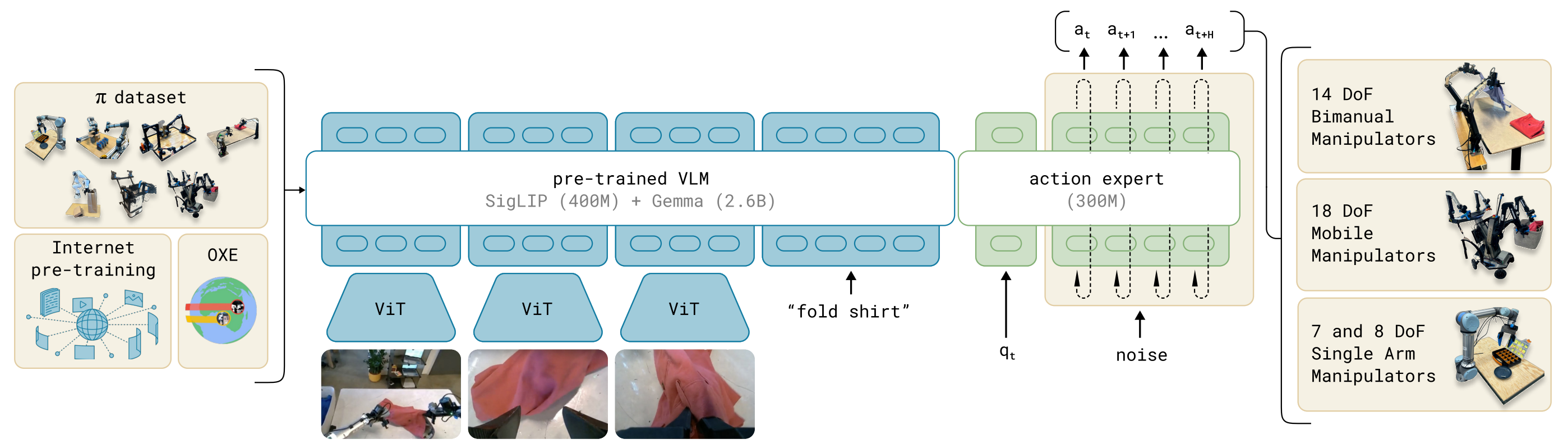
概述 传统机器人策略模型往往局限在单一任务或平台，难以跨场景泛化。与此同时，大规模 视觉-语言模型（VLM） 已展现出卓越的语义理解与任务指令解析能力。如果能将 VLM 的语义理解能力 与 Flow Matching 的连续动作建模能力 结合，有望构建具备泛化与实时性的机器人通用控制器。 Pi0 （π0）正是这样一个探索：基于 PaliGemma（3B 参数 VLM） 作为感知与语义主干，结合 Flow Matching 动作生成器，实现语言到多机器人动作的端到端建模。它借鉴了大语言模型的“预训练 + 微调”范式，把互联网级别的语义知识和机器人操控数据结合起来，从而实现跨平台、跨任务的通用机器人控制。 我们此前分析了VLM、Flow Matching原理，掌握这些之后理解Pi0是非常简单的。 原理 结构 模型结构主要有VLM主干+ Action Expert动作专家构成。 VLM主干：基于 PaliGemma（一个 3B 参数的 VLM），继承互联网规模的图像+语言知识。 Action Expert（动作专家）：额外的子网络，负责用 Flow Matching 方法预测连续动作向量。 模型的输入包括观测的多视角RGB图像、语言指令、机器人自身状态（关节角、传感器），经过模型处理后输出为高频动作序列（每秒50HZ动作chunk），这些动作控制单臂、双臂、移动操作臂等多类机器人。 训练 我们训练的目标是让$A_t^0 \sim \mathcal{N}(0, I)$ ——>$A_t$（真实动作），希望模型学会如何把一个“噪声动作”流动成一个真实的动作。就像扩散模型是“噪声 → 图像”，这里是“噪声动作 → 专家动作”。 在训练的时候要让噪声动作流向真实动作，我们需要构建一个路径，这里依旧使用的是直线路径。 $$ A_t^\tau = \tau A_t + (1-\tau)\epsilon, \quad \epsilon \sim \mathcal{N}(0,I) $$ 这个公式跟我们在Flow Matching文章中的训练公式是不是一样的。我们在噪声动作$\epsilon$和真实动作$A_t$之间，采样一个"插值点"。$\tau $表示时间的进度，当$\tau = 0$时完全是噪声，当$\tau = 1$时完全是真实动作，这个就构造了一条噪声到动作的直线路径。 我们的目标是要让模型告诉我们"从当前点$A_t$应该往哪个方向移动，才能逐渐靠近真实动作"，因此就是在计算在每个时间速度。 $$ u(A_t^\tau \mid A_t) \triangleq \frac{d}{d\tau} A_t^\tau $$ 代入公式可得： $$ \frac{d}{d\tau} A_t^\tau = A_t - \epsilon $$ 而论文中成$u(A_t^\tau \mid A_t) = \epsilon - A_t$，只是方向约定相反，本质上没有差异。上面的公式，目标速度就是噪声 - 动作，它定义了“流动的方向”。就像在地图上，目标向量场就是指路的“箭头”。这样得到了真实的速度场，我们就可以在训练的时候计算损失了。 $$ L(\theta) = \mathbb{E}\big[ | v_\theta(A_t^\tau, o_t) - u(A_t^\tau \mid A_t) |^2 \big] $$ $v_\theta$是神经网络（Action Expert），输入 当前 noisy action + 观察$o_t$，输出预测的速度场。损失函数就是 预测的速度场 vs 真实的目标速度场 的均方误差 (MSE)。训练目标：让模型学会在任意中间点给出正确的“流动方向”。 推理 $$ A_t^{\tau+\delta} = A_t^\tau + \delta v_\theta(A_t^\tau, o_t) $$ 推理生成也比较简单，从噪声动作$A_t$开始，每次迭代一步：输入当前的$A_t^\tau $和观察的$o_t$，接着模型给出速度场，就沿着这个方向走一步（步长$\delta$），然后按照这个步骤重复迭代，最终得到真实的动作$A_t$。和扩散模型不同：这里不需要几十/上百步，只要 ~10 步 ODE 积分，就能得到高质量动作，适合机器人实时控制。 参考： https://arxiv.org/abs/2410.24164

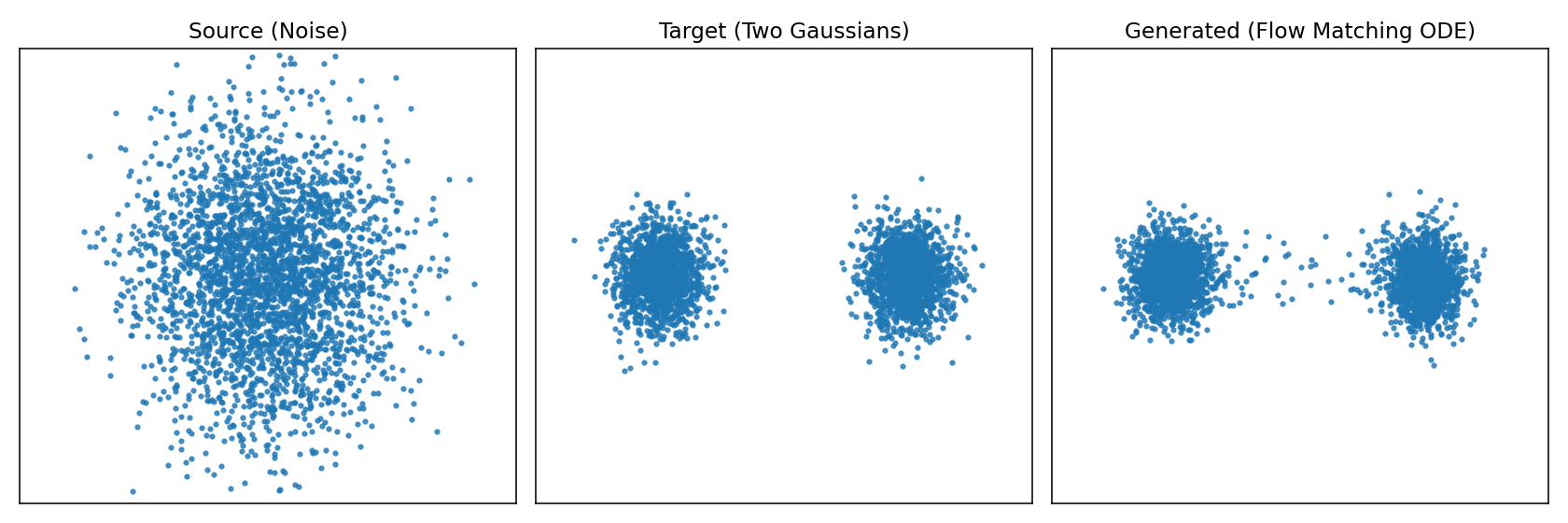
背景 上一篇文章分析了diffusion扩散模型。diffusion扩散模型做法是加噪声、再一步步去噪，训练过程复杂，还需要 carefully 设计噪声调度。 Flow Matching提出了更直接的方式：与其通过一大堆离散的“加噪/去噪”步骤，不如直接学习一个连续的流动 (flow)，让点从噪声“顺滑地流动”到目标数据。 原理 把生成过程看作流体运动，想象有一堆水滴（噪声），通过一个力场，它们会被推动、流动，最后聚集成目标形状（真实分布的数据）。Flow Matching从物理学角度学一个"速度场"，让数据点从"源分布(噪声)"流动到"目标分布(真实数据)"。 如图所示左边是源随机点云，中间是目标形状，右边是实际使用模型生成的形状。为了更直观的体会再来看下图从源分布逼近目标分布的过程。 左图就是源分布的点在不同时间应该朝那个方向运动直到最终的目标分布，右图是不同时刻让这些点应该往哪个方向进行流动速度场。 接下来看看数学怎么表示，我们希望从源分布$p_{src}$(比如高斯分布)按照流动的方式到目标分布$p_{data}$，那么方式就是在每个时间$t$为每个点$x$都指定一个速度$v_\theta(x,t)$，这样在不同时间就知道点该往哪里动，那么点的轨迹就完全确定了。在数学上点的位置$x(t)$随着时间变化，那就是速度场向量，即常微分方程 $$ \frac{dx}{dt} = v_\theta(x, t) $$ 左边的$\frac{dx}{dt}$描述的是随时间的变化率，右边$v_\theta(x, t)$就是我们要学习的"速度场",它给出"$t$时刻，位置$x$应该往哪里动"。 总结一下Flow Matching 里速度场写成 ODE，是因为它给出“点的位置随时间的变化率”，这正是常微分方程的定义，生成过程就是解 ODE，从噪声轨迹流到数据。 推理 模型要做的事情就是要预测出下一个时间刻应该往哪里走，输出是一个速度场；推理的过程就是解常微分方程ODE。 输入：当前位置$x \in \mathbb{R}^d$，当前时间$t \in [0,1]$。 输出：模型计算输出当前的速度向量，即$\frac{dx}{dt} = v_\theta(x,t)$。 更新：根据速度向量$v_\theta(x,t)$通过积分公式把所有时间段速度累积起来得到最终点$x(1)$。 $$ x(1) = x(0) + \int_{0}^{1} v_\theta(x(t),t)\,dt $$ 直观理解就是神经网络提供"切线方向"，积分就是"把所有切线拼起来"，形成完整的轨迹，从噪声走到目标分布。 但实际过程中我们用离散的数值方式，比如欧拉法，如下： 时间从$t$=$0$到$t$=$1$，分成若干小步（比如50或100步），在每一步按照上面公式更新。 输入：当前的位置$x_k$和当前时间步$t_k$。 输出: 模型预测计算速度向量场$v_\theta(x_k, t_k)$。 更新：通过欧拉法更新公式更新下一步位置$x_{k+1} = x_k + v_\theta(x_k, t_k)\Delta t$ 每一步模型计算出速度向量$v_\theta(x_k, t_k)$然后根据公式进行更新下一步的位置，新位置=旧位置+速度x时间步长；$v_\theta(x_k, t_k)\Delta t$计算每次迭代的移动距离（速度x时间），这就是基本的欧拉积分法，直观的意义是在短时间$\Delta t$内，点会沿着速度场方向前进一点。不断的进行多步迭代，从$x_0$出发，逐步得到$x_1$，$x_1$，$x_2$，$x_3$，....，$x_k$，当$k$=$K$时，$t_K$=$1$，就得到最终的$x(1)$。 怎么理解$t_k$、$x_k$、$\Delta t$？ $t_k$是第$k$步对应的时间点，如果flow matching的时间区间是[0,1]，我们把它切成$K$个小步（如50或100步），每个时间点就是$t0$=$0.00$，$t1$=$0.01$；$\Delta t$是时间步长如把时间区间[0,1]均匀分成100步，那么$\Delta t$=$1/100$=$0.01$；$x_k$是表示在$t_k$时的点（或点云），初始时从高斯噪音采样到。 下面再来一个直观图展示了Flow Matching推理的过程。 灰色箭头：代表速度场$v_\theta(x_k, t_k)$，告诉每个位置的点应该往哪里走。上图设定的目标是(2,2)。 绿色点：初始$x(0)$来自噪声分布即源分布。 红色叉：表示目标位置，代表数据分布的一个样本区域。 蓝色折现轨迹：数值积分结果，点一步一步验证速度场北推向目标。 训练 我们希望模型学会把源分布$p_{src}$流动到目标分布$p_{data}$；换句话说就是有$x_0 \sim p_{\text{src}}$，输出目标点$x_1 \sim p_{\text{data}}$我们要训练一个速度场网络$v_\theta(x_k, t_k)$，让它指导点$x_t$沿正确的路径从$x_0$——>$x_1$。 要训练行动轨迹需要知道真实轨迹这样才能和实际预测值做比较求损失，而训练的关键却正好是不知道真实的速度场。那如何构建训练的目标了？可以设计一个简单的"参考轨迹"，如直线路径$x_0$——>$x_1$。 $$ x_t = (1 - t)x_0 + tx_1 $$ 给定输入样本$(x_0 \sim p_{\text{src}},x_1 \sim p_{\text{data}})$，其中$x_0$是源随机位置，$x_1$是目标位置。在训练的时候我们自己定义一条直线路径$x_0$——>$x_1$，我们不能一步到位，而是要有一个流动的过程。 这条直线路径上的真实速度公式对$t$求偏导，而恰巧速度是一个常数（始终指向目标点$x_1$）。 $$ u^\star = \frac{dx_t}{dt} = x_1 - x_0 $$ 既然速度方向就是一个常数$x1-x0$，为什么不直接一步把$x1$变成$x0$，而要搞成连续流动了？ 如果一步到位公式就变成$x_1 = x_0 + (x_1 - x_0)$，相当于直接跳到目标点，完全不需要ODE、积分、网络。但问题在于训练时我们有配对的$(x_0, x_1)$，所以能写下$(x_1-x_0)$，而推理时了我们只有$x_0 \sim p_{\text{src}}$,并不知道该对应那个$x1$，因此不能一步到位，因为没有$x_1$可直接计算。 最后我们训练目标就是网络预测的速度$v_\theta(x_k, t_k)$，损失就网络预测的速度$v_\theta(x_k, t_k)$与真实的速度$x_1-x_0$的均方误差。训练完成之后，网络就学会了在任何位置$x_t$、时间$t$给出正确的速度场。 $$ \mathbb{E}\Big[ || v_\theta(x_t, t) - (x_1 - x_0) ||^2 \Big] $$ 源码示例 为了加深理解，程序实现一个最小的 Conditional Flow Matching（直线路径的 Rectified Flow）示例，学习时间条件速度场 vθ(x,t)，把二维标准高斯源分布推到左右两个高斯簇的目标分布。训练后输出两张图：训练损失曲线 cfm_loss.png，以及三联静态图 cfm_overview.png（源/目标/生成）。 # -*- coding: utf-8 -*- # Flow Matching demo: source N(0,I) -> target: Two Gaussians (left & right) # 输出： # 1) cfm_loss.png（训练损失） # 2) cfm_overview.png（三联图：Source / Target / Generated） # 依赖：pip install torch matplotlib import time, warnings warnings.filterwarnings("ignore", category=UserWarning, module="matplotlib") import numpy as np import torch, torch.nn as nn, torch.optim as optim import matplotlib matplotlib.use("Agg") import matplotlib.pyplot as plt # ------------------------- 配置 ------------------------- device = torch.device("cuda" if torch.cuda.is_available() else "cpu") torch.manual_seed(0) XLIM = (-4.0, 4.0) YLIM = (-3.0, 3.0) # ------------------------- 数据分布 ------------------------- def sample_source(n): return torch.randn(n, 2, device=device) def sample_target(n): sigma = 0.35 means = torch.tensor([[-2.0, 0.0], [2.0, 0.0]], device=device) idx = torch.randint(0, 2, (n,), device=device) mu = means[idx] return mu + sigma * torch.randn(n, 2, device=device) # ------------------------- 模型：速度场 v_theta(x,t) ------------------------- class VelocityNet(nn.Module): def __init__(self, h=64): super().__init__() self.net = nn.Sequential( nn.Linear(3, h), nn.ReLU(), nn.Linear(h, h), nn.ReLU(), nn.Linear(h, 2), ) def forward(self, x, t): return self.net(torch.cat([x, t], -1)) # ------------------------- 训练（CFM，直线路径） ------------------------- def train_cfm(steps=2000, batch=512, lr=1e-3): net = VelocityNet().to(device) opt = optim.Adam(net.parameters(), lr=lr) loss_hist = [] t0 = time.time() for s in range(1, steps + 1): x0 = sample_source(batch) x1 = sample_target(batch) t = torch.rand(batch, 1, device=device) xt = (1 - t) * x0 + t * x1 u = x1 - x0 pred = net(xt, t) loss = ((pred - u)**2).mean() opt.zero_grad(set_to_none=True) loss.backward(); opt.step() loss_hist.append(float(loss)) if s % 200 == 0: print(f"[{s}/{steps}] loss={loss:.4f}") print(f"Train time: {time.time() - t0:.2f}s") return net, loss_hist # ------------------------- 采样（生成轨迹） ------------------------- @torch.no_grad() def generate_traj(net, n=3000, steps=60): x = sample_source(n) dt = 1.0 / steps traj = [x.cpu().numpy()] for k in range(steps): t = torch.full((n,1), (k + 0.5) * dt, device=device) x = x + net(x, t) * dt traj.append(x.cpu().numpy()) return traj # ------------------------- Matplotlib 工具 ------------------------- def save_loss(loss_hist, path): plt.figure(figsize=(6, 3.6)) plt.plot(loss_hist) plt.title("Training Loss (CFM)") plt.xlabel("step"); plt.ylabel("MSE") plt.tight_layout(); plt.savefig(path, dpi=140); plt.close() print(f"Saved {path}") def save_overview(src, tgt, gen, path): fig, axes = plt.subplots(1, 3, figsize=(12, 4)) titles = ["Source (Noise)", "Target (Two Gaussians)", "Generated (Flow Matching ODE)"] for ax, title, pts in zip(axes, titles, [src, tgt, gen]): ax.scatter(pts[:, 0], pts[:, 1], s=5, alpha=0.75) ax.set_title(title) ax.set_xlim(*XLIM); ax.set_ylim(*YLIM) ax.set_xticks([]); ax.set_yticks([]) plt.tight_layout(); plt.savefig(path, dpi=140); plt.close() print(f"Saved {path}") # （已移除 GIF 相关工具与依赖） # ------------------------- 主程序 ------------------------- if __name__ == "__main__": # 训练 net, loss_hist = train_cfm(steps=2000, batch=512, lr=1e-3) save_loss(loss_hist, "cfm_loss.png") # 数据与生成 src = sample_source(3000).cpu().numpy() tgt = sample_target(3000).cpu().numpy() traj = generate_traj(net, n=3000, steps=60) gen = traj[-1] # 三联静态图 save_overview(src, tgt, gen, "cfm_overview.png") # （已移除 GIF 生成步骤） print("All done.") （1）模型结构 模型结构为VelocityNet，使用了一个小型 MLP，输入 3 维（x 的 2 维 + t 的 1 维），输出 2 维速度向量。结构为Linear(3,64) → ReLU → Linear(64,64) → ReLU → Linear(64,2)。forward(x,t) 直接拼接 [x, t] 后送入网络。这里没有使用时间位置编码。 （2）训练过程 训练函数为train_cfm(steps=2000, batch=512, lr=1e-3)，具体过程如下： 1) 每步采样源 x0 ~ source 和目标 x1 ~ target，独立均匀采样 t~U(0,1)。 2) 构造直线桥接点 xt = (1 - t)x0 + tx1。 3) 定义理想恒定速度 u = x1 - x0（常速，不依赖 t）。 4) 让网络在 (xt, t) 上预测 pred = vθ(xt,t)，用 MSE(pred, u) 作为损失。 5) Adam 更新一次；每 200 步打印当前损失。 6) 返回训练好的 net 与 loss_hist。 直观理解，虽然 u 依赖 (x0, x1)，但模型只观察 (xt,t)。训练学到的是条件期望 E[x1 - x0 | xt, t]，也就是让网络在直线路径上学会把点往“正确方向”推的平均速度。这是直线路径 CFM 的核心思想。 （3）采样 采样函数为generate_traj，从源分布采样 n 个起点，设步长 dt=1/steps。用无梯度模式按欧拉法更新：对每步 k，用中点时间 t=(k+0.5)dt 预测速度 vθ(x,t)，然后 x ← x + vθ(x,t)dt。记录每一步的点云到列表，返回整个轨迹（列表元素是 numpy 数组）。主程序中只使用最后一步作为“生成结果”。 （4）主流程 最后就是主流程先调 train_cfm 进行训练，保存 cfm_loss.png。分别采样 3000 个源样本 src 与目标样本 tgt。生成 n=3000、steps=60 的轨迹 traj，并取 gen = traj[-1] 作为最终生成样本。保存 cfm_overview.png，展示源/目标/生成的对比。 整体主要的实现点为 目标路径：x_t = (1 - t) x0 + t x1，直线连接源与目标。 理想速度：dx/dt = x1 - x0，使点沿直线以恒定速度匀速前进。 学习目标：在 (xt,t) 上回归 u = x1 - x0 的条件期望；推断时只需网络与当前状态，无需知道具体的 x0 或 x1。 数值积分：使用欧拉法简单高效；采用中点时间能略微减小离散误差。

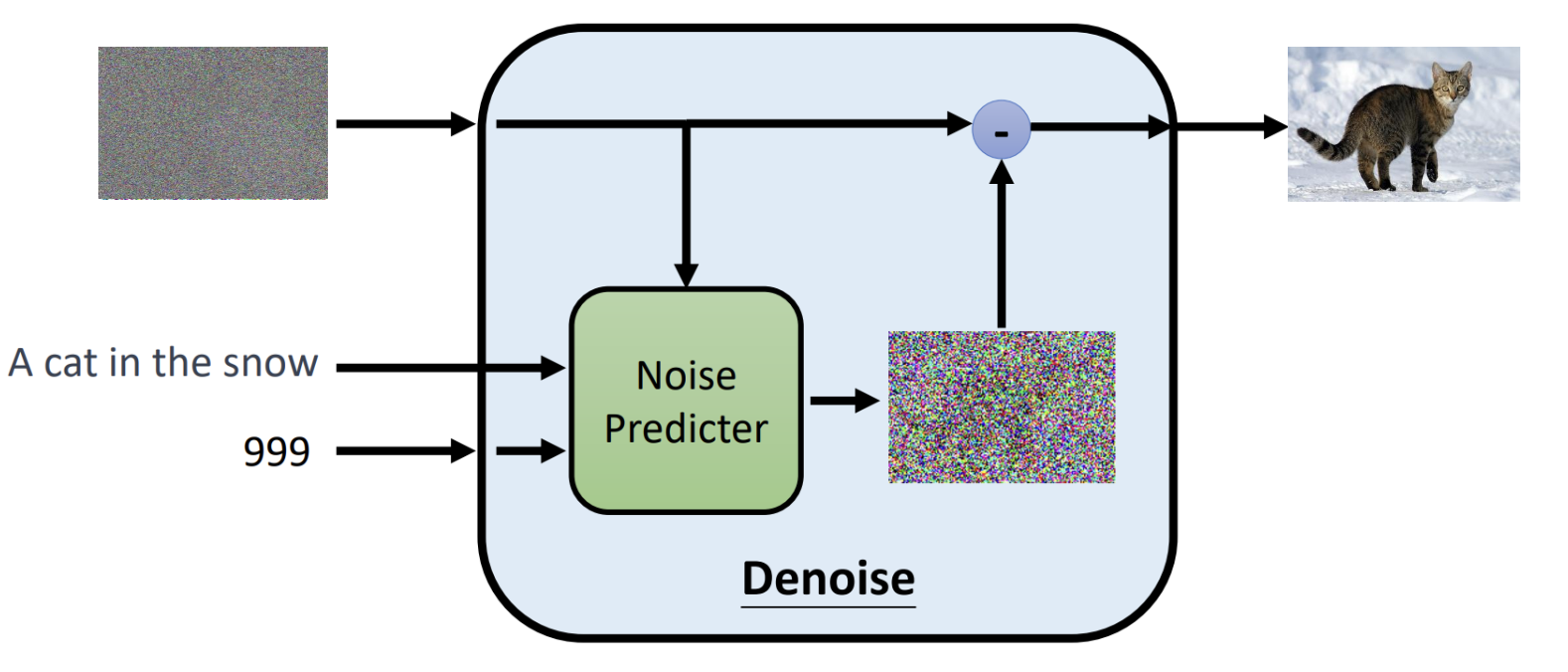
概述 图像生成是当下研究的热点，diffusion是一种人工智能领域图像生成的基础模型，当下Stable diffusion、DALL·E、MidJourney文生图模型的基座都使用了diffusion。 diffusion扩散模型属于生成式模型，生成图像不是正向从0到1构成图像而是反向的预先生成一个随机的噪声图中然后根据文本提示词逐渐的去噪"扣"出图像。主要思想是先训练一个权重模型，把一张清晰照片弄得越来越模糊（加入噪声），然后把模糊的图片融合文本提示词作为输入去训练一个模型学会“擦亮它”，反向恢复成清晰图像。训练完成后，就得到了模型的权重，那么使用这个权重模型只要给一副完全随机的“噪点图”和要生成图片的提示词，它就能一步步去掉噪声，变出一幅崭新、逼真的图片。 借用米开朗基罗雕刻"大卫像"时说的"我在大理石中看见天使，于是我不停地雕刻，直至使他自由”。而diffusion也是这样的原理，通过随机生成的一个噪声图片，结合输入的文字去掉噪音恢复到你想象的照片样子。 工作原理 推理 （1）输入阶段 输入阶段有3个输入信息，分别是随机噪声图像、文本提示、时间步。 随机噪声图像：最开始随机生成一个高斯噪声的图片。 文本提示：告诉模型，想要生成的内容是什么。 时间步：指明当前是去噪第几步，模型是一个多步迭代去噪的过程。按照数字依次递减进行迭代，数值越小去噪强度越弱。 （2）模型处理 核心组件是Noise Predictor（一般是一个U-Net结构神经网络），输入的带噪图像$X_{t}$、时间步$t$、以及提示文本通过Noise Predictor预测出这张图里有多少噪声，生成一张噪声图片$\epsilon^\theta(x_t, t, c)$。 （3）输出阶段 将输入-减去预测出的噪声图片就得到最后的去噪图片了，$x_{t-1} = x_t - \epsilon^\theta(x_t, t, c)$。 （4）迭代 迭代一轮得到一个降噪图片之后，接着将输出的降噪图片作为输入的带噪图片按照之前的步骤进行重复，直至$t$=$T$（比如$1000$）一直迭代到$t$=$0$得到最终的图像。当所有步骤完成后，随机噪声逐渐被“洗掉”，生成的就是一张符合条件描述的清晰图像。 下面是推理过程的算法伪代码 初始化：$x_T \sim \mathcal{N}(0, I)$从标准高斯分布中采样一个随机噪声向量（或噪声图像），作为生成过程的起点。 迭代循环：从$t$=$T$到$t$=$1$逐步迭代，每次去掉一部分噪声。如果$t$>$1$，额外采样一个噪声向量$z\sim \mathcal{N}(0, I)$。如果$t$=$1$，则$z$=$0$，即最后一步不加噪声。 核心公式：先去掉预测的噪声（括号里面的部分）得到更接近干净数据的样子，接着在进行缩放调整(除以$\sqrt{\alpha_t}$)，最后加一点随机噪声$\sigma_t z$来保持生成的多样性。 输出：当循环结束时，最终的$x_0$就是最终生成的清晰图像了。 对于核心公式的参数这里稍微补充一下 参数 $\epsilon_\theta(x_t, t)$是预测的噪声； 参数$\alpha_t$取值范围是$0$~$1$，控制在第$t$步中保留多少原始图像信息加入多少噪声，当$\alpha_t$接近$1$时几乎保留全部信息，噪声小；当值趋于0时，原始信号衰减就大，噪声比例高； 参数$\bar{\alpha}_t$累积乘积参数，表示从第$1$步到$t$步累积保留原始信息的比例。 参数$\sigma_t z$随机扰动项，保持采样的多样性。 训练 训练模型我们需要把模型的输出结果和真实值进行比较才能进行梯度下降找到网络权重，那该如何设计准备训练结果和真实值的数据？ diffusion模型的核心是要预测出图片的噪声分布然后减去预测的噪声得到真实的输出照片。以上图第一步进行说明，使用原始的图片，通过随机生成一个噪声图($x_{1}$)迭加作用到原始图片上这样就得到了模型的带噪声的输入图像，然后融合文本、时间步模型前向计算得到噪声图($x_2$)。已经知道了真实的噪声图是$x_{1}$，那么计算$x_{1}$和$x_{2}$的相似性就可以计算出损失了。 训练过程中关于图片-文本可以从Lion平台上获取，通过上面步骤取样照片然后不断加强噪声得到越来越模糊的图片送入模型预测进行计算迭代权重，让模型学会真正准确预测每一步中"加进去的噪声"，训练完成之后，模型学会了如何"识别噪声"，在推理时就从纯随机噪声$x_T$出发，通过文本提示词反向迭代去噪得到最终的想要的照片。 论文中的伪代码如下： repeat：表示循环执行训练过程。 采样数据：$x_0 \sim q(x_0)$从真实数据分布$q(x_0)$中采样一个训练样本比如一张猫。 随机采样时间步:$t \sim \text{Uniform}({1, \dots, T})$随机挑选一个扩散的时间步$t$,确保模型能在不同噪声水平都学会去噪。 采样噪声：$\epsilon \sim \mathcal{N}(0, I)$从标准的高斯分布中采样一份噪声，用于后续得到到原始图片上。 梯度下降更新参数：计算预测噪声和真实噪声$\epsilon$的均方误差。 模型 本章节简要说一下业界文生图模型，其结构可以总结为以上3个部分，文本编码器、生成式模型、解码器。 文本编码器：将用户输入的文本提示通过预训练的文本编码器如CLIP Text Encoder将自然语言转化为向量表示。 生成式模型：将编码的文本向量和噪声图像noisy latent作为输入，然后逐步迭代去噪。这里的模型如有diffusion、autoregressive等。输出是压缩到更低维的"潜在空间"。 解码器：将生成式模型的输入Latten Representation通过解码器还原最终生成清晰图像。生成式模型一般输出的是压缩的低维潜在空间，这样可以降低每一步迭代的计算量，最终加一个解码器来将其还原。 下面是stable diffusion、DALL-E、Imagen的模型结构图，核心组成都是上面3个部分，这里就不过多阐述了。 stable diffusion DALL-E Imagen 本文主要来自李宏毅Diffusion Model原理解析的笔记。

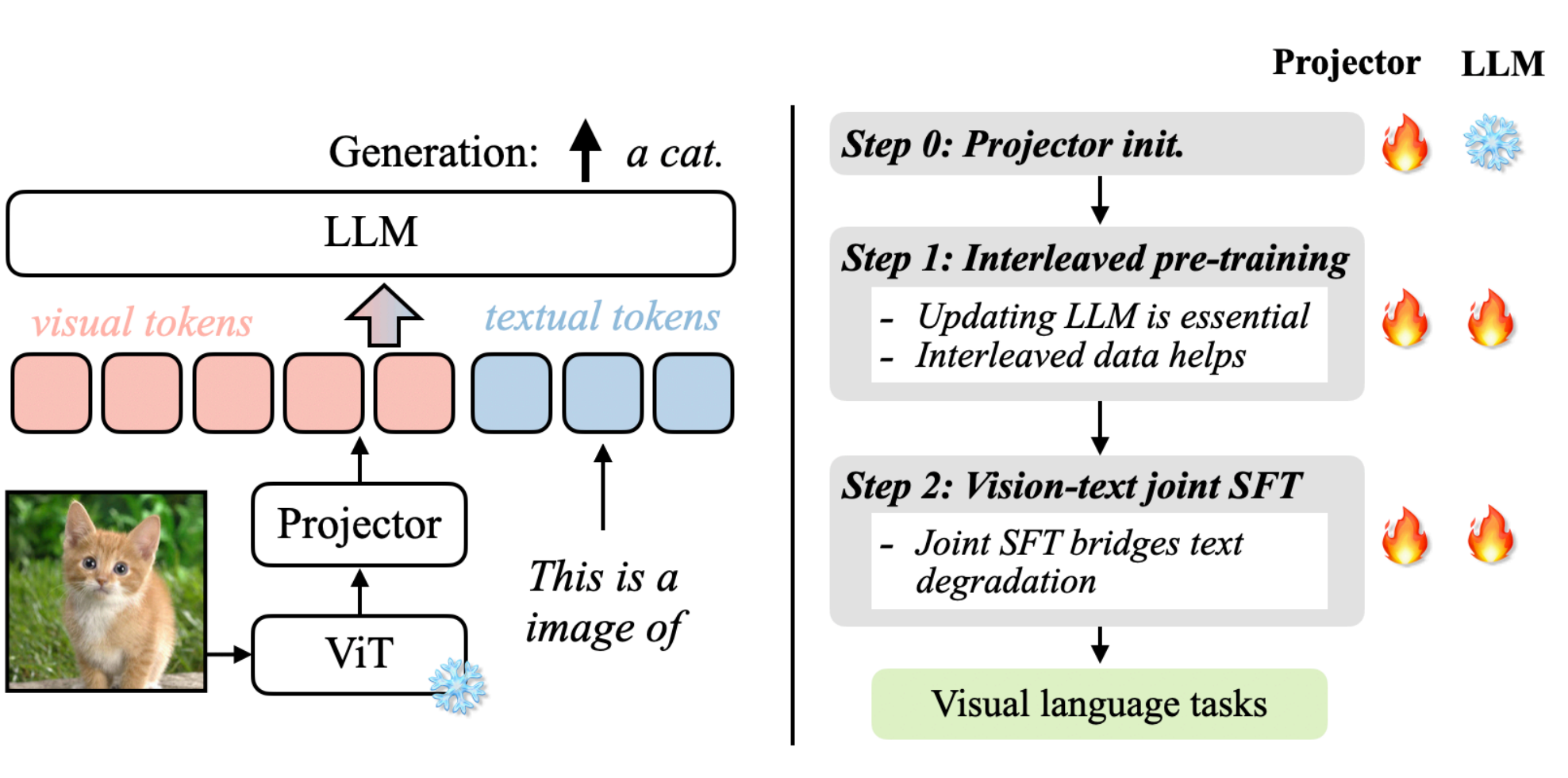
VLM与LLM 如果说我们有一张图片、一个图表想让大模型来帮忙理解那应该要怎么实现了？ 标准的LLM语言大模型只能处理文本序列，是不能够读取图像的，如果没有办法将视觉的数据转换为LLM能够理解的形式，那么LLM是无法处理的。需要注意的是我们这里说的LLM并不是transformer，LLM指的是大语言模型如DeepSeek，GPT，Qwen，其是使用了transformer架构应用，而transformer是一种神经网络架构。LLM的token专门指的是文本token来自Tokennizer其输入是字节流，而transformer不一定是文本单位，可以是任何序列元素如词、图像（上节说的ViT）等。 要解决语言大模型理解图片，那么这就是视觉-语言大模派上用场了。回顾一下我们此前说的ViT视觉大模型，是不是就是用提取图像特征的，因此本章节我们要介绍的正是视觉大模型与语言大模型的融合：vision language model，即视觉-语言大模型。 视觉-语言大模型是视觉大模型+语言大模型的结合，其主要有哪些用途？核心用处是让 AI 能够“读图如读文”，在多模态场景下实现理解、生成和交互，如下示例： 内容理解：多模态的问答VQA，比如给一张图让大模型理解图片里面描述了什么，让其识别图片里物体、动作、关系，自动生成图片说明（Image Captioning）等等。 信息获取与搜索：给一张图找对应的描述，或给一句话找到相关图片（比如电商商品搜索）以及搜索引擎文字搜图或图搜文字等。 模型结构 发展到今天有很多的视觉-语言大模型，各自都有自己的架构实现。我们先以VILA为例来说明一下视觉-语言大模型的关键组件，上图来自论文：VILA: On Pre-training for Visual Language Models。 上图我们先来分析一下其运作流程，可以分为左右两部分：左图可以看成是怎么跑起来的(数据流推理/前向)，右图是如何训练的步骤。 数据流 左图：数据流推理 ViT: 首先将图像送入ViT视觉编码器，提取出视觉特征。 Projector：因为ViT输出的特征维度可能与LLM词嵌入维度不一致，所以这里也需要通过一个线性层/小MLP做映射，把视觉特征空间转换为LLM的嵌入空间为，为上图的visual tokens。 token融合：文本提示经过tokenizer转换为text tual tokens与visu tokens在同一序列中进行拼接或交错输入到LLM。 LLM生成：进入LLM后，视觉与文本已在同一token流中就可以共同参与计算注意力，最后输出最后的结果a cat。 训练策略 右图：训练策略 训练主要分为3个阶段，projector初始化，交错式预训练、监督微调，主要涉及projector和LLM模型参数更新，火焰代表参数会被更新，雪花代表冻结不更新。 Step 0 Projector初始化：只训Projector，LLM冻结，通常ViT也冻结，目的是先把视觉特征大致对齐到LLM词向量空间，避免一上来就动LLM破坏语言能力。 Step 1 交错式预训练：同时更新Projector与LLM，在包含图像-文本交错（图像token混在文本序列里）的数据上做自回归训练。更新LLM才参数才能让LLM学会"在文本上下文中使用视觉特征"；图像和文本的输入进行交错能够教会模型跨模态对齐与引用。 Step2 监督微调：联合微调projector与LLM，输入数据是指令时的多模态问答/对话。这样可以把能力对齐到agent任务上，同时避免LLM文本能力退化。 小结 通过VILA架构为例，我们大概了解了VLM视觉-语言大模型的架构，我们总结下VLM模型架构主要可以分为三大部分： 视觉编码器：将视觉输入转换为结构化的数值表示，提取语义信息。如基于transformer架构的ViT，将图像分割成小块，通过transformer编码全局和局部特征；如传统基于CNN卷积神经网络ResNet，擅长提取局部纹理特征。 投影器：视觉和文本嵌入必须对齐到一个共享的多模态嵌入空间。通常由一个较小的模块完成，称为投影层或融合层：常见的实现方式有MLP通过全连接层转化维度(如DeepSeek-VL)；交叉注意力机制通过动态关联图像区域与文本token(如llama 3.2 vision)，增强空间理解。 LLM：接收图像+文本融合后的多模态输入，生成自然语言响应（如描述、答案、推理）。 QA1:这里的投影器projector与此前我们分析ViT中的projection线性投影有什么不一样？ ViT中的projection作用是将图像分割后的每个小块线性映射为固定维度向量(token)作为transformer编码器的输入;而VLM的projector是将视觉编码器(如ViT)输出特征映射到语言大模型（LLM）的文本嵌入空间，解决跨模态语义鸿沟。一个是作用在ViT的输入映射为transformer的标准输入另外是一个作用再ViT的输出映射为LLM的标准输入。 QA2:为什么要将图像和文本进行融合多模态嵌入空间？ 多模态嵌入空间是VLM具备推理能力的关键，通过在同一潜在空间表示视觉和文本信息，主要有以下优势： 上下文感知：使不同模态之间能够进行丰富的交互，这意味着模型能够将文本概念（例如，“公交车”、“十字路口”）准确地与视觉特征信息（公交车位置、颜色、十字路口）连续起来。 语义连接：将抽象的文本概念与具体的视觉示例进行对齐。例如模型不仅将“行人”理解为单词，还将其视为图像中可视觉识别的实体。 跨模态推理：允许模型在不同模态之间进行推理，回答复杂的视觉问题，进行逻辑推断，或检测微妙的视觉-文本差异。 模型预训练 训练史 先来看看视觉识别训练的发展，可以划分为5个阶段：传统机器学习与预测，深度学习从零训练与预测，监督式预训练、微调与预测，无监督预训练、微调与预测，视觉语言模型预训练与零样本预测。稍微总结一下各自特点。 传统机器学习与预测：需要人工设计学习特征。 深度学习从零训练与预测：从零自己标注大量数据（因为没法迁移），从零训练。 监督式预训练、微调与预测：预训练复用公开标注好的海量数据（可以迁移，所以可用公开别人标注好的海量数据），从零标注一些少量数进行微调。 无监督预训练、微调与预测：预训练数据集再扩大了，可以直接爬取互联网的数据进行训练，但还是需要从零标注一些少量数据进行微调。 视觉语言模型预训练与零样本预测：不需要进行微调了，那么也不需要标注的数据集了，做到零样本。 VLM的预训练与零样本预测方式与过往的相比，对下游视觉识别任务上实现零样本，去掉了微调的过程，那么这种方式就可以有效利用大规模的网络数据。 预训练架构 因为VLM有很多种模型架构，因此预训练的架构也有区别，下面列出常见的几种。 双塔式架构：视觉和文本模态分别通过独立的编码器处理（如ViT处理图像、BERT处理文本），模态交互仅发生在编码后的特征层面，在最后进行融合，典型的模型有CLIP、ALIGN等。 双分支架构：在独立编码器基础上引入动态交互模块，支持灵活切换双塔或单塔模式，实现任务自适应融合如VLMo、Mini-Gemini等。 单塔式架构：像和文本输入共享同一Transformer编码器，通过交叉注意力机制实现早期深度融合，典型的模型如ViLT，FLAVA等。 预训练目标 前面阐述了当前视觉-语言大模型通常采用预训练与零样本预测的方式。那么在视觉语言大模型（Vision-Language Models, VLM）中我们的预训练目标是什么了？所谓预训练目标（Pre-training Objectives）是让模型从海量无标注图文对中自动学习跨模态关联的核心机制。这些目标的目的建立视觉与语言模态的语义对齐，为下游任务（如视觉问答、图像描述）提供通用表征基础。而当前的训练目标大致可以分为3类：对比目标、生成目标、对齐目标。 对比目标：让模型学会"配对"正确的图文，并区分错误的组合，比如正样本匹配的图文对（如猫图 + “一只猫”），模型需让它们的特征向量高度相似；负样本不匹配的图文对（如猫图 + “一辆汽车”），模型需让它们的特征向量差异巨大。计算的损失函数为所有配对的相似度误差（如 InfoNCE损失），指导模型调整参数，代表模型有CLIP、ALIGN等，该方式一般适用于零样本分类、图文检索的模型。 生成目标：让模型“填空”或“创作”，通过预测缺失内容学习深层语义。具体输入通过mask遮住文本或图像，训练模型让其复原得到网络权重。该方式一般应用与图像描述、视觉问答（VQA）的模型。 对齐目标：让模型能够把句子的词精准对应到图中位置，要求最高。比如用目标检测框出识别图中的物体（如汽车），与文本中的词精确关联。该方式一般用于目标检测、语义分割等场景。 VLM模型 当前已经出现了很多视觉语言模型，各自的模型都具有独特的功能，在视觉语言研究领域和实际应用上扮演着重要的贡献，除了在第2章节我们介绍的VILA外，这里我们在本章节再补充举例几个进行简要说明一下。 CLIP 上图是CLIP模型，是一个典型的双塔式视觉-语言模型，由视觉编码器（ViT）和文本编码器（Transformer）等核心组件构成。通过预训练对比目标的方式学习实现图像与文本的跨膜态对齐，其核心创新点在于无需任务特定训练，直接利用自然语言提示（Pormt）完成零样本预测，支持识别训练数据中为出现的新类别。 从图中我们可以看成可以分为3个阶段，对比预训练、创建零样本分类器、零样本预测。 （1）对比预训练阶段 输入是海量的图文对，如图片输入狗+文本输入"pepper the aussie pup"。 编码：文本编码器（如transformer）将文本嵌入向量，图像编码器（如ViT/ResNet）将图像嵌入向量。 目标：图文预文本嵌入向量的点积度量图文相似性。通过对比损失(infoNCE)计算图文相似度矩阵。拉近匹配对（如对角线深蓝块，如狗图与"狗"文本），推远不匹配对（非对角线浅色块，如狗图与“汽车”文本）。 （2）创建零样本分类器 输入：新任务的类别标签（如 "dog", "bird", "car"）。 处理：将标签转化为提示文本（如 "a photo of a {label}"），文本编码器生成所有标签的文本嵌入向量。 输出：得到一组文本嵌入，构成无需训练的分类器权重（传统模型需图像数据训练分类头） （3）零样本预测 输入：一张新图像（如鸟的图片）。 处理：图像编码器生成图像嵌入向量（左侧绿色向量），计算该向量与所有类别文本嵌入相似度。 输出：选择相似度最高的文本标签作为预测结果（如输出 "a photo of a bird"）。 总结一下就是，通过上面的预训练，将配对的图文靠近，非配对的原理，学到语义对齐的公共空间，这样在在推理时把“类别标签”也写成一句话，当作“文本查询”；用这句“查询”去和图像向量比相似度，谁最像选谁。 LLaVA LLaVA是把视觉模型提取的图像特征通过一个映射层转成语言模型能理解的 token，然后和用户的语言指令一起输入到大语言模型（LLM），从而实现图像理解与多模态对话。其架构主要由Vision Encoder（视觉编码器）、Projector（视觉特征投影）、Language Instruction（语言指令输入）、LLM大模型几个组件构成，跟我们前面第2章节总结的结构类似，这里就不过多阐述了。下面简要说一下流程： 输入图像：输入的图像通过Vision Encoder提取特征$Z_{v}$。具体来说，预训练用的是CLIP模型的视觉编码器ViT-L/14。 特征投影：通过projector W提取的图像特征$Z_{v}$转换成LLM能够处理的token表示$H_{v}$。 输入指令：用户文本$X_{q}$转换为token表示$H_{q}$。 拼接输入：将[$H_{v}$,$H_{q}$]拼接一起送入LLM。 语言生成：LLM输出语言响应$X_{a}$，完成图像理解+问答。 LLaVA 是一个用于对齐视觉和语言数据以处理复杂多模态任务的复杂模型。它采用独特的方法，将图像处理与大型语言模型融合，以增强其解释和响应图像相关查询的能力。通过利用文本和视觉表示，LLaVA 在视觉问答、交互式图像生成以及涉及图像的基于对话的任务中表现出色。其与强大语言模型的集成使其能够生成详细描述，并协助实时视觉语言交互。 参考： 1. An Introduction to Vision-Language Modeling 2. Vision Language Transformers: A Survey 3. Understanding Vision-Language Models (VLMs): A Practical Guide 4. Guide to Vision-Language Models (VLMs)

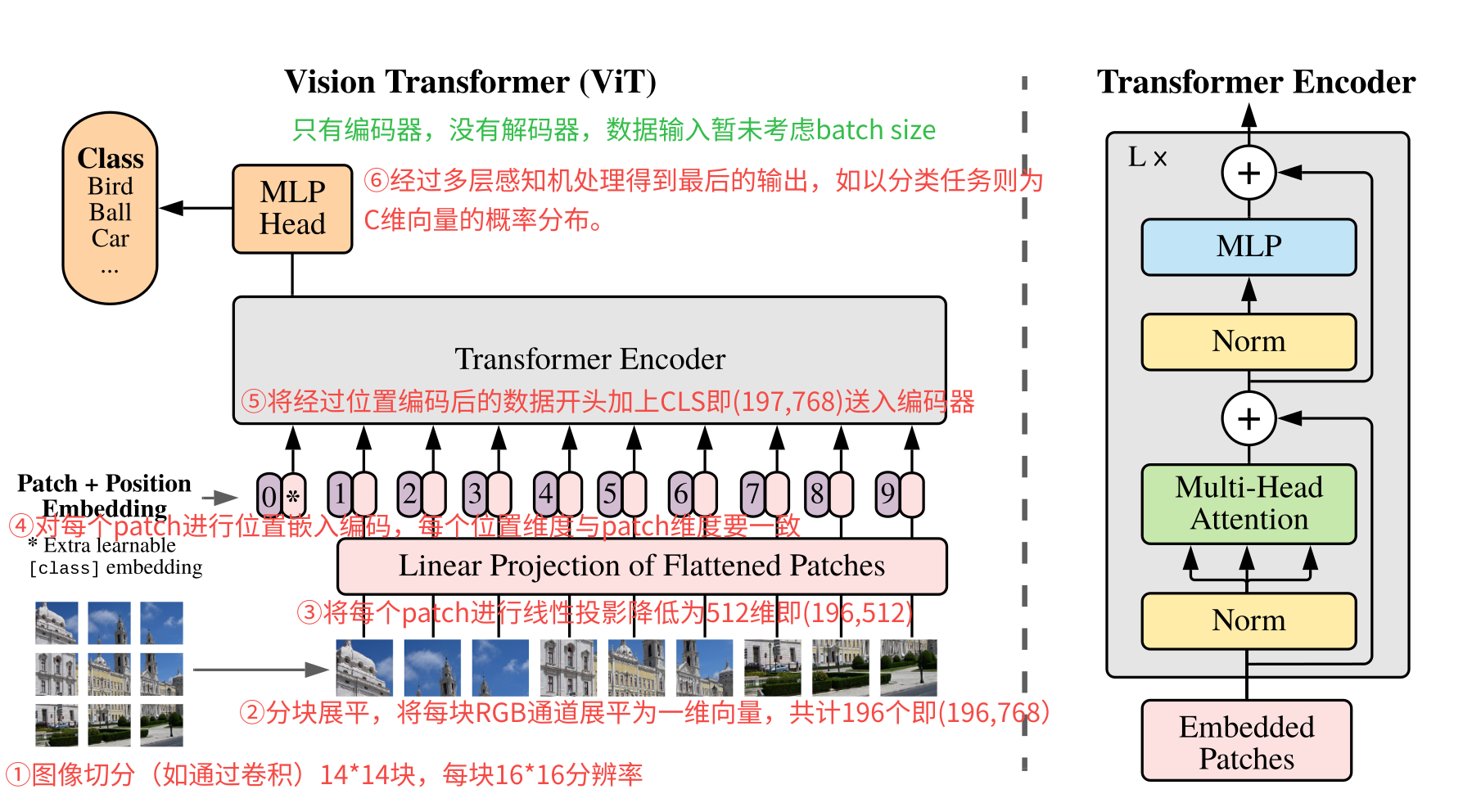
背景 计算机视觉领域，一直都是卷积天下。传统的卷积神经网络(CNN)依赖于卷积核提取局部特征，效果很好，但是也有一些不足，如需要人工设计卷积结构包括卷积核大小和层数，另外就是难以捕捉全局的依赖关系。 transformer最早更多的是应用在NLP领域的架构，用注意力机制来捕捉长距离的依赖。那把transformer应用在视觉领域了，会有什么效果吗？而在2021年发表的https://arxiv.org/abs/2010.11929这篇论文就是使用transformer应用在图像识别的领域。 论文中提到基于transformer使用监督学习方式训练模型进行图像分类时，在中等规模数据集（如ImageNet）上如果没有使用强正则化其准确率略低于同等规模的ResNet。但是当加大数据集（1400W至3亿张图像）训练时，发现其识别水平超越了现有技术。 模型概览 上图就是整个ViT模型结构了，对transformer比较熟悉的，整个结构就很简单了。可以发现只有transformer encoder没有transformer decoder。 这里先整体看看其流程步骤： 图像切块：原图输入为224x224分辨率的图像，将其切分为14x14共196块的（如使用卷积），每块大小的分辨率为16x16。 分块展平：将每块为16x16分辨率的patch展平为一维向量，共计有196个这样的向量。由于每块是RGB 3通道图像，因此向量维度为16x16x3= 768，按照RGB排布进行展开为一维向量。因此最后的数据形状为（196，768）。 线性投影：对每个patch的向量乘以一个权重矩阵，映射到D维的embedding空间，这个D维跟transformer输入维度一致（默认是512）。因此经过转换后的数据就变成了（196,768）->(196,512)。 位置编码：对经过线性映射的patch加上位置编码，每个patch一个位置向量，其向量的维度与patch维度一致，总的位置编码矩阵为(196,512)。将这个位置编码与经过线性映射的进行相加得到输入。 编码输入：经过位置编码后的输入然后在最开始加上了[CLS]向量送入编码器。因此输入的数据为(197,512)。如果算上批量数据最后就是(B,197,768)。B为batch size，197为patch数，512为embedding维度。 编码输出：最后经过多层感知机MLP得到最后的输出，如果是分类任务的话，就是(B,C)结果，B为batch size，C为类别数。也就是结果每行就是一个概率分布。 常见问题 （1）图像是如何切分展平的？ 以输入尺寸3x224x224的RGB图像为例，块大小为16x16,因此块的数量为14x14=196个块。每个块3x16x16被拉成一维向量长度为16x16x3=768，也就是每个块被展平为768维向量，一共有196个块，也就是说转换为(196,768)的矩阵。 （2）每个patch为什么要展平？ 主要是transformer的输入要求，因为transformer是序列处理器，其输入必现是一维的向量序列，而图像分块后得到的每个块是二维矩阵。还记得在transformer实现文章中吗？输入的是(seq,d_model)，seq为token的数量，而d_model为每个token嵌入的向量。当然这里的图像最后还需要经过映射降维跟这里的d_model保持一致，这样才能输入到transformer的编码器中。 （3）线性投影有什么作用？ 主要有两个作用，其一是图像分块展平后得到的是高维稀疏向量(如16163=768)，包含了大量冗余信息如局部宽高、噪声等，缺乏高层语义表达，数据量大，计算量也大，线性投影是一个可训练全连接权重矩阵，可以提取保留关键局部特征；其二是为了适配transformer输入结构，Transformer要求输入为固定维度向量序列（如 D=512）。线性投影统一所有图像块的输出维度，确保自注意力机制可计算。 （4）这里的位置编码与transformer的有什么不同吗？ ViT中的位置编码使用的是自适应位置编码，transformer中用的是正余弦固定公式，因为ViT中的输入序列位置一般都有限，因此用1D的可学习的位置编码即可，这个位置编码是一个可学习的参数矩阵，初始化为全0，在训练过程中通过反向传播自动优化。 （5）输出的MLP与transformer FFN有什么不同吗？ 基本一样的，FFN是前馈神经网络的统称，MLP是具体的前馈神经网络具体实现特指全连接网络。 （6）最后的输出是什么样的？ ViT最后的输出结构根据实际任务需求有关，如果是图像分类任务，在最终输出是[CLS] token向量经 MLP Head映射后的logits（未归一化的类别分数），形状为 [B, K]（K为类别数）； （7）整个处理流程数据变化是怎么样的？ 处理阶段 输入形状 操作 输出形状 示例值（B=64） 原始输入 [B, C, H, W] — [64, 3, 224, 224] Patch分块 + 展平 [B, C, H, W] 卷积核尺寸=步长=P（如 16×16） [B, N, P²·C] [64, 196, 768] 线性投影（Patch Embedding） [B, N, P²·C] 全连接层映射至目标维度 D=512 [B, N, D] [64, 196, 512] 添加 Class Token [B, N, D] 序列前拼接可学习的 [CLS] 向量 [B, N+1, D] [64, 197, 512] 位置编码叠加 [B, N+1, D] 加可学习位置编码 E_{pos} ∈ ℝ^{1×(N+1)×D} [B, N+1, D] [64, 197, 512] Transformer 编码器 [B, N+1, D] 多头自注意力（MSA） + MLP 前馈网络 [B, N+1, D] [64, 197, 512] 分类头输出 [B, D]（仅取 [CLS]） 全连接层映射至类别数 K [B, K] [64, 1000]

概述 框架 以翻译作为例子，从宏观角度理解大模型，可以把大模型视为一个黑匣子，它可以输入一种语言然后输出另外一种翻译语言，如下图所示。 如果将模型稍微展开一下，模型分为encoders和decoders两部分。为什么要分为编码器和解码器了？主要是从以下动机考量。 条件生成需求：在机器翻译、摘要、对话等条件文本生成任务重，需要读懂输入再逐步输出目标序列这两个事情的约束不同。读懂输入需要双上下文（每个词即要看到左也要右），也就是说要在上下文中去理解，没有因果约束。而生成输出需要的是自回归，因为是预测，只需要看历史不能偷看未来，这就需要因果掩码的自注意力。 结构解耦：把理解和生成拆开，分别最优各自的注意力、掩码和结构，这样更清晰也更高效。 encoders是有多个相同的encoder堆叠在一起形成，decoders也是一样。 encoder和decoder在结构上都是相同的，但是他们不共享权重。下图是encoder和decoder微观结构。 编码器将输入的序列X=(x1,......,xn)映射到连续表示序列Z=(z1,.....zn)，然后将Z给到解码器。解码器每次生成一个元素的符号输出序列(y1,......yn)。解码器在每一步都是自回归的，在生成下一步时将先前生成的符号作为额外输入。 编码器：编码器由N=6个相同层堆叠组成。每层都有两个子层，第一个子层是多头注意力（Multi-Head Attention），第二个是简单的按位置完全连接的前馈网络（Feed Forward）。在两个子层的周围分别采用残差连接（Add），然后再进行层正则化（Norm）。每个子层的输出是LayerNorm(X+Sublayer(X))，其中Sublayer(X)是由子层本身实现的函数。为了促进这些残差连接，模型中所有子层以及嵌入层都产生维度为$d_{model}$=512的输出。 解码器：解码器也是由N=6个相同层堆栈组成，除了每个解码器层中的两个子层之外，解码器还插入了第三个子层Masked Multi-Head Attention，该子层对编码堆栈的输出执行多头注意。与编码器类似，在每个子层周围采用残差连接然后正则化。与编码器不同的是，这里增加了Masked Multi-Head Attention修改于Multi-Head Attention，防止当前的输入元素关注到后续的位置元素，这种掩码加上输出嵌入偏移一个位置，确保位置i的预测只能依赖小于i的位置的已知输出。 流程 下面以一个中文句子翻译为英文为例，简要说明步骤。 word embedding： 输入的句子分词得到["我", "有", "一个", "苹果"]，然后将每个词进行词嵌入（算法这里不阐述）转换为6维的向量。 positional encoding：每个词进行位置编码，生成相关的位置信息。每个词的向量维度与词embedding维度一致。 transformer输入X： X=embedding + positional embedding，shape形状为(seq_len,d_model)，其中seq_len为输入token数量，这里为4，d_model为词embedding向量维度。 编码输出矩阵E：输入X经过编码器后，经过自注意力分数等计算最后输出矩阵E将作为解码器的输入。矩阵E与输入的X形状一致。 解码输出：解码器的输出根据输入一个一个产生的，最开始的时候输入"BOS"代表开始将输出"I"，输入"BOS I"输出I have，输入"BOS I have"输出"I have an".......。 mask：在解码器内部有一个mask，其主要的作用是让生成步骤仅以来历史信息，不能访问未来的词。因为decoder是一个一个词生成的，自注意力层天然会计算序列中所有位置间的关联，若不施加约束，模型可能尝试为当前未生成的空白位置分配权重，生成第3个词时，模型默认会为第4、5等未来位置计算注意力权重（尽管这些位置尚无实际内容）。 输入 transformer的输入是一个多阶段的过程，核心的目标是将原始序列的数据转换为包含语义和位置信息的向量表示，这里重点分为word embedding和positional encoding。 word embedding 在进行word embedding之前，需要先把输入句子进行分词，得到离散的序列。如"我有一个苹果" → ["我", "有", "一个", "苹果"]。 所谓word embedding词嵌入，就是将句子拆分的每个词映射到固定维度的向量，transformer论文中默认的向量维度为512，本文的示例是6维。如下： 我：[0.2, -0.3, 0.7, 0.1, -0.5, 0.4] 有：[0.6, 0.2, -0.8, 0.3, 0.1, -0.4] 一个：[-0.4, 0.9, 0.2, -0.1, 0.3, 0.6] 苹果：[0.5, -0.7, 0.4, 0.8, -0.2, 1.1] 关于转换映射的有很多方式，如随机初始化+训练学习的方式，或者word2vec，Glove等外部嵌入算法，这里就先不研究了。 positional encoding 自注意力机制本身不具备序列顺序的感知能力，而自然语言的语义高度以来次序，比如"猫爪老鼠"和"老鼠抓猫"含义就完全相反。因此需要显性的为每个词助于顺序信息，通过给每个位置进行编号，让模型感知词序。 而在transformer中，使用是的正弦函数和余弦函数给每个词生成唯一向量，其中偶数的向量维度使用正弦函数计算得到，基数使用余弦函数计算得到。其公式如下： $$\begin{aligned} PE_{(pos, 2i)} &= \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) \ \ PE_{(pos, 2i+1)} &= \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) \end{aligned}$$ 变量说明 $pos$：词在序列中的位置（从0或1开始，示例中为1~4，如"我"是1，"有"是2，“一个”是3，"苹果"是4） $i$：向量维度索引（从0开始，文档示例中$d_{\text{model}}=6$，故$i=0,1,2$） $d_{\text{model}}$：模型隐藏层维度，也是word embedding向量维度（示例中为6，原始论文中为512） 下面基于d_mode=6说明计算过程，以第一个词"我"为例，计算其过程。 已知条件 $pos=1$（第1个词的位置） $d_{\text{model}}=6$（向量维度为6） $i=0,1,2$（对应3对奇偶维度） 维度0（偶数位，$2i=0$）：$PE_{(1,0)} = \sin\left(\frac{1}{10000^{2×0/6}}\right) \approx 0.8 \quad $ 维度1（奇数位，$2i+1=1$）：$PE_{(1,1)} = \cos\left(\frac{1}{10000^{2×0/6}}\right) \approx 0.5 \quad $ 维度2（偶数位，$2i=2$）：$PE_{(1,2)} = \sin\left(\frac{1}{10000^{2×1/6}}\right) \approx 0.1 \quad$ 维度3（奇数位，$2i+1=3$）：$PE_{(1,3)} = \cos\left(\frac{1}{10000^{2×1/6}}\right) \approx 1.0 \quad $ 维度4（偶数位，$2i=4$）：$PE_{(1,4)} = \sin\left(\frac{1}{10000^{2×2/6}}\right) = \approx 0.0 \quad$ 维度5（奇数位，$2i+1=5$）：$PE_{(1,5)} = \cos\left(\frac{1}{10000^{2×2/6}}\right) \quad 1.0 $ 最后得到"我"的positional encoding为[0.8,0.5,0.1,1.0.0.0,1.0]。 使用正弦函数、余弦函数进行编码有以下好处。 相对位置可学习：对于任意位置偏移$k$，$PE_{pos+k}$可表示为$PE_{pos}$的线性组合（利用三角函数的和角公式），使模型能轻松学习相对位置关系。 无界序列适应：公式基于指数函数衰减，对任意长度的序列（远超训练时的最大长度）均能生成有效编码，避免了学习型位置编码的泛化性问题。 数值稳定性：正弦/余弦函数的值域固定在$[-1,1]$，与词嵌入向量相加后不会导致数值范围剧烈波动，有利于模型训练稳定。 注意力机制 在transformer中最关键的就是Multi-Head Attention,本小节先来重点分析其实现原理。Multi-Head Attention由多个Scaled Dot-Product Attention组成。 注意力函数可以描述为将查询（Query）和一组键值对（Key-Value）映射到输出，其中查询、键、值和输出都是向量，输出计算为加权和。 Scaled Dot-Product Attetion 其核心的公式就是如下： $$ \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V $$ 对于Scaled Dot-Product Attention自下而上计算的流程如下： MatMul：输入查询矩阵 Q（目标序列）与键矩阵 K（源序列）进行矩阵乘法，主要用于计算原始相关性的分数。$\text{Scores} = QK^T$ Scale：缩放的目的是防止计算的分数导致softmax梯度消失，因此对结果进行缩放。$\text{Scaled Scores} = \frac{\text{Scores}}{\sqrt{d_k}}$。 Optional Mask：mask用于遮挡无效位置（如未来词或填充符），训练是设置-inf，只有在解码器的时候用。 SoftMax：对计算分数进行归一化，输出注意力权重权重概率分布。$\text{Weights} = \text{softmax}(\text{Masked Scores})$ MatMul：前面的QK计算得出了目标词在句子中的哪些词相关性比较大，也就是得到一个注意力分数，最后根据注意力分数做加权求和到最后的目标词上下文信息向量。$ \text{Output} = \text{Weights} \cdot V$ 接下来我们展开按照流程来分析一下。 计算QKV Transformer中引入Q（Query）、K（Key）、V（Value）三元组的设计是注意力机制的核心创新，使用QKV本质是实现动态语义的聚集。传统的传统RNN/CNN在长距离建模时存在固有缺陷，CNN依赖局部卷积核，RNN受制于顺序编码，无法动态关注全局关键信息。而使用QKV三元组模拟"信息检索系统" Query（查询）：表示当前需要关注的内容,需要“寻找什么信息”（如翻译中"apple"要找出"苹果"的语义需求）。 Key（键）：描述源信息的特征标签（如中文词"苹果"的语义属性）。 Value（值）：存储实际待提取的信息本体（如"苹果"的词嵌入向量）。 自注意力机制就是用q去找相关的k，得到注意力分数，然后通过注意力分数去从v中提取信息。 如翻译“I have an apple”时，生成“apple”的Query会去找跟（“苹果”）相关的key计算高相似度，然后用得到的K取提取Value（“苹果”的语义向量），实现精准跨语言对齐。 使用Q MatMul K的方式可以量化查询的需求与源特征的匹配程度，最后在MatMul上V是因为做最终的提取。 既然Q MatMul K是量化查询需求与源特征的匹配程度，那么每个词一般都是在句子中去理解的，所以每个词都需要去计算在句子中其他词的关联。 每个都需要与句子中的其他进行相关性计算，各自得到一个输出。如a1最终计算出得到b1，a2计算得到b2......。 （1）以单个词为例说明运作流程 下面以a1为例： 首先a1先自己计算出q1，q1=Wq a1，其中Wq为权重参数。 其次句子中所有词a1,a2,a3,a4分别乘Wk计算各自得到k1,k2,k3,k4。 接着q1分别与k1,k2,k3,k4分别做点积计算得到a11,a12,a13,a14。 最后在对a11,a12,a13,a14做softmax得到最终的结果。a'11,a'12,a'13,a'14。 为什么要做softmax了？ 归一化概率：将原始分数（可能为任意实数）转换为概率分布，使得所有权重和为1，便于后续的加权求和操作（即用这些权重来加权值向量）。 增强区分度：softmax 的指数运算会放大高分数的影响，同时抑制低分数。这样，模型可以更加关注最相关的键，而忽略不相关的键。在图中，如果某个 α{1,i} 较大，经过 softmax 后其对应的 α'{1,i} 会远大于其他较小的分数对应的权重，从而实现选择性聚焦。 在对softmax之前还要进行一次scale这里就不周赘述了。 a'11,a'12,a'13,a'14即为a1对句子中每个词的注意力分数，计算出值后就可以根据其值从序列里面抽取出了重要的信息，根据a'11,a'12,a'13,a'14可知输入的词向量哪些跟与a1相关性大，接下来即可根据关联性（即注意力分数）抽取重要的信息。 将向量a1~a4分别乘以Wv权重得到新的向量v1,v2,v3,v4，将其中的每一个向量分别乘以注意力分数a'xx,再把结果加起来。 $$ b_1 = \sum_{i} \alpha'_{1,i} v_i $$ 如果a1和a2关联性强，即a'12的值就很大，那么在做加权和以后，得到的b1就越接近与v2，所以谁的注意力分数越大，谁的v就会主导抽取结果。同理可以计算出b2,b3,b4。 （2）以矩阵乘法角度说明运作流程 上面的过程是单个词的计算过程，但是实际在自注意力模型的运作过程中，是通过矩阵乘法的方式计算的，这样效率才高，接下来看看从矩阵乘法的角度理解运行过程。 因为每个词都要产生qkv，即每个ai都要乘以权重参数Wq得到qi，那么可以把这些ai合并起来当做一个矩阵，即把a1到a4拼接起来，看成一个矩阵I，矩阵I有4列，其中每一列都是自注意力模型的输入。把矩阵I乘以矩阵Wq，就可以得到Q。其中Wq则是权重参数，Q则可以看成q1~q4的拼接。 同理产生k和v的操作跟q一模一样，计算得到K，V矩阵。 通过两个Q与K转置相乘就可以得到注意力分数的矩阵A，然后将A经过softmax得到A'。 最后使用注意力分数A'提出V，得到最终的输出矩阵O，即b1~b4的拼接。 最后总结下，自注意力模型输入是一组向量，将这些向量拼接起来得到I，让后将I分别乘以三个矩阵Wq,Wk,Wq，得到另外三个矩阵QKV，将Q乘以K的转置得到A，然后对A在做一些处理得到A'，A'为注意力分数矩阵，将A'乘以V提取出特征，最后得到自注意力的输出O。 Multi-Head Attention 论文中阐述，与其使用一套维度为$d_{model}$的单头注意力，还不如把输入的Query、Key、Value各自用不同的、可学习的线性投影经过注意力机制映射出$h$份版本，每份的维度更小，计为$d_{k}$和$d_{v}$。 在每一份（也就是每个头）上各自并行计算注意力，得到$d_{v}-$维的输出，然后再把所有头的输出沿特征维度拼接，再做一次线性投影到得到最终的输出。 为什么要做多头？多头可以“同时在不同表示子空间里看信息”。一个头往往只能聚焦一种关系（比如短距依赖），多个头能并行关注不同关系（长距、句法、语义等）。如果只有单头，容易把多种关系“平均混在一起”，表达力受限。 多头注意力会把输入进行降维值C/h，这样每个头的输入维度就为C/h。为什么使用"多头+降维"而不是"多头不降维"，主要会是考虑如果每个头都保持默认的输入C维，h个头拼接后会是[B, L, h·C]，参数量与计算复杂度都膨胀 h 倍，不经济。标准做法让每头维度变为 C/h，拼接回到 C，因此总计算/参数量与单头同量级，但表达力更强（多视角、子空间解耦）。 下面是来说明一下多头注意力机制是如何计算的，下面省略了输入降维的过程。 如上图，先把a乘以一个矩阵得到q，然后再把q乘以另外两个矩阵得到q1,q2。qi1和qi2代表的有两个头，表示要查询两种不同的相关性，那么既然有两个q，k，v也得需要两个，同理得到各自的两个k，v。 关于多头注意力机制的计算跟上一节的计算类似，各自的头计算各自的，如上图是计算头1，下图是计算头2。 通过各自头的计算，那么将会得到各自头的一个输出bi1,bi2，最后需要将bi1和bi2拼起来，先乘以一个矩阵进行变换得到bi，再送到下下一层。 encoder 编码器有多个相同的子编码器叠加而成，最小单元的子编码器由Multil-Head Aattention、Add & Norm、Feed Forward这几个组件构成，Multil-head Attention前面已经解释了，接下来重点分析剩余模块的流程。为表述方便后面的编码器都默认指最小单元的编码器。 Add & Norm Add & Norm在编码器一个block中出现了两次，首次出现是位于 Multi-Head Attention（橙色模块）的输出端，再次出现是位于 Feed Forward（蓝色模块）的输出端。如下图： （1）残差连接 残差连接的作用是在深层网络中，梯度在反向传播时可能会消失或爆炸。残差连接通过将输入直接加到函数输出上（即 F(x) + x），提供了一个恒等映射的路径。这使得梯度在反向传播时可以直接流过，从而缓解了梯度消失的问题，使深层网络训练成为可能。 Add操作是残差连接（Resudual Connection），其公式 $$ \mathbf{y} = \mathcal{F}(\mathbf{x}, {\mathbf{W}_i}) + \mathbf{x} $$ （2）层归一化 层归一化的作用是在残差连接之后，数据的分布可能会发生变化，可能会导致后续层的学习变得困难，使用层归一化能够重新调整数据分布（如将每一层的输出归一化为均值为0，方差为1），从而加速训练并提高模型的泛化能力。 层归一化计算公式步骤如下： 这里使用的是层归一化而非批归一化，主要是可以独立处理每个样本，应对变长序列输入，同时对小批量训练不依赖批量统计量。 为什么Add&Norm要成对使用？ 每个主要计算层后面都有Add & Norm，形成了一种模式：计算层 -> Add & Norm。这样，每个计算层的输出在传递给下一层之前都会被重新调整，使得模型在训练过程中保持稳定。如果只有残差连接而没有归一化，那么随着层数的增加，输出的尺度可能会不断增长，导致训练不稳定；如果只有归一化而没有残差连接，则可能无法解决深层网络中的梯度消失问题。 Feed Forward 先来看看什么是Feed Forward，前馈神经有两层全连接神经网络组成，中间使用非线性激活函数（通常是ReLU），数学表达式如下： $$ FFN(x) = \text{ReLU}(xW_1 + b_1)W_2 + b_2 $$ （1）特征扩展，将特征维度从512扩展至2048 $$ \boxed{ h_i = \text{ReLU}( \underbrace{x_i}{1 \times 512} \underbrace{W_1}{512 \times 2048} + b_1 )} $$ $x_i$：位置$i$的输入向量（$1 \times 512$） $W_1$：扩展层权重矩阵（$512 \times 2048$） 前面输入attention结果本质上计算是加权平均，都是线性操作，这里引入ReLu非线性变化，使模型能学习更复杂的函数映射。同时升维可以在高维空间捕捉更细微模式。 （2）进行特征压缩，将特征从2048压缩回512 $$ \boxed{ y_i = \underbrace{h_i}{1 \times 2048} \underbrace{W_2}{2048 \times 512} + b_2 } $$ $h_i$：ReLU激活后的特征向量（$1 \times 2048$） $W_2$：压缩层权重矩阵（$2048 \times 512$） 最后再从高维进行降维，保持与后续模块的兼容性。 总结一下FFN的作用有如下： 高纬投影：将输入映射到高维空间（如512→2048），捕获更复杂的特征组合。 非线性激活：引入非线性（如ReLU），打破线性变换限制，增强模型表达能力。 低维还原：将特征压缩回原始维度，保持与后续模块兼容性。 encoder block Multi-Head Attention、Add & Norm、Feed Ward构成了一个encoder block。 每个encoder block接入输入矩阵Xnd，并输出一个矩阵Ond，再把输出的O当做输入传递给下一个encoder，通过多个encoder的叠加，最后一个encoder block输出的就是编码信息矩阵E，用于送入到解码器中，就完成transformer的Encoder。 decoder decoder与encoder大致的结构类似，但是也有差别主要由Masked Multi-head Attention、Multi-head Attention、Add & Norm、Feed Forward组成，这里唯一不一样的是Masked Multi-head Attention，接下来分模块介绍一下关键流程。 Masked Multi-head Attention Masked Multi-head Attention通过一个掩码来阻止每个位置选择器后面的输入信息。 Multi-head Attention自注意力输入一排向量，自己输出另一排向量，这一排向量中的每个项链都要看过完整的输入后才能决定。如上图必现根据a1,a2,a3,a4的所有信息来输出b1。 而掩码多头注意力则不再看右边的部分，如下图。 在产生b1的时候，只考虑a1的信息，不再考虑a2,a3,a4的信息。在产生b2的时候，只考虑a1,a2的信息，不再考虑a3,a4的信息，在产生b3的时候，只考虑a1,a2,a3的信息，不再考虑a4的信息，只有在阐述b4的时候，才考虑整个输入序列的信息。 下面是Multi-head Attention产生b2的过程，b2需要和a1,a2,a2,a3的qkv信息计算得到b2。 而如果是Masked Multi-head Attention，b2只需要拿q2和k1、k2计算注意力，最后只计算v1和v2的加权和，不管a2右边的部分，则计算过下。 为什么在注意力机制中加上掩码了？ 因为解码器的输出是一个一个产生的，只能考虑左边已经生成的部分，而没有办法考虑未生成的右边部分。举个例子，先有得a1,再有a2，接下来是a3，然后是a4。这个跟编码器中的self-attention不一样，编码器中的是a1,a2,a3,a4一次性输入模型，编码器一次性处理输出。正因为解码器这个特性，现有a1，才能预测输出a2，再有后面的a3,a4，所以当我们在计算b2时，a3,a4实际是还没输出的，所以没有办法考虑a3,a4。 Multi-head Attention 第二个Mult-head Attention也称为交叉注意力，结构组成与编码器没什么差别。主要的差异点计算输入，解码器的第二个Multi-head Attention（交叉注意力）输入，这个注意力层的Query来自解码器前一层（通常是解码器的第一个Masked Self-Attention层）的输出，而Key和Value则来自编码器的最终输出（即最后一个编码器层的输出）。因此，该注意力层的目的是让解码器在生成当前输出时能够关注到输入序列的相关部分。 输出 transformer最后的输出层是linear层和softmax层。 linear层：将解码器输出的高维语义向量映射到词汇表空间，输入为(batch_size, seq_len, d_model)，输出为(batch_size, seq_len, vocab_size)，主要的作用是将抽象语义转换为具体词汇的匹配分数（Logits）。 softmax层：将Logits转换为概率分布，输入为Logits矩阵，输出为(batch_size, seq_len, vocab_size)的概率张量，满足概率约束（和为1），支持损失计算与生成任务。 Linear层 Linear层主要作用是计算解码器向量与每个词嵌入的点积，得到词汇表中每个词的原始匹配分数，计算公式为。 $$Logits = X \cdot W^{T} + b$$ X：解码器最后一层输出（形状 [batch_size, seq_len, d_model]，例：[1, 4, 6]） W：权重矩阵（形状 [vocab_size, d_model]，例：50000×6） b:偏置项（可选） 最终的输出是词汇表中每个词的概率（形状 [batch_size, seq_len, vocab_size]，例：[1, 5, 10000]），假设这里的词库为10000个。 如下： logits = [ "I": 8.76, "have": 7.23, "a": 5.89, "an": 6.54, "apple": 7.91, ... # 其他99995个词 ] softmax层 $$P(\text{word}i) = \frac{e^{\text{logits}_i}}{\sum{j=1}^{V} e^{\text{logits}_j}}$$ V： 词汇表的大小 指数运算：放大高分优势。 如下 "I": 0.38, "have": 0.22, "an": 0.18, "apple": 0.15, "a": 0.04, ... # 其他词概率极小 总结一下： 时间步 解码器输入 Linear层Logits示例 Softmax后概率 选定词 1 <bos> I=9.8, He=1.2,... I=0.99,He=0.03,... I 2 <bos> I have=8.5, has=0.5,... have=0.97,has=0.02,.... have 3 <bos> I have an=7.9, a=2.1,... an=0.95,a=0.04 an 4 <bos> I have an apple=9.5, app=3.2,... apple=0.99,app=0.03,.... apple 到这里，transformer的原理就分析完了。 参考如下： 书籍：深度学习详解 https://arxiv.org/abs/1706.03762 https://jalammar.github.io/illustrated-transformer/ https://zhuanlan.zhihu.com/p/338817680

基本原理 简单总结一下什么是ACT算法。传统的机器算法过程是观测关节位置J1经过模型预测动作A2然后执行，观测到J2预测数A3，观测到J3遇到A4依次类推，这样就有一个问题，假设预测出的A2跟实际相比偏差就比较大那么对应的观测到的J2就偏离比较大。如果要连续预测K步，就要连续采集K步，缺点就是误差会累积同时预测效率也比较低。那么对于ACT算法是怎么进行优化的了？ ACT算法是一下观测连续的K个动作，然后预测出K个动作，这样相对于传统算法效率就提升了K倍。同时也可以解决累积误差，计时K个连续的动作中，有某个动作偏差比较大，但是整体经过模型就会弱化不至于累积。假设K是10 ，简单举个例子理解过程，T0时刻观测到J1数据（开始时只有一个数据），模型直接预测数10个动作序列，等机器按顺序依次执行完这10个动作后，模型下一次就直接把这10个动作当做输入然后预测下一批的10个动作，依次类推。 基于transformer的动作分块（ACT）架构。分为训练模式和测试模式。 当为训练模式是，ACT为左图的编码器+右图的解码器。左图可以理解为一个CVAE的编码器，将关节序列、动作序列、CLS经过transformer编码压缩为风格变量Z。然后将Z再加上采集的摄像头数据、关节序列作为输入给到右边的解码器最终输出动作序列。 当为测试模式时，左图丢弃不再，只需要使用右图的部分，输入为摄像头数据、关节序列、Z（被简单设置为0，表示先验的平均值）。可以这么理解Z为CVAE模型中的风格，经过训练后，Z已经让模型的参数定型，在后续的测试过程中就不需要了，因为参数已经固定了就不用了。 以lerobot的机械臂为例，个人理解关节序列指的是从臂的舵机位置，而动作序列是主臂的舵机位置。 动作分块 动作分块Action Chunking机制，传统机器人每执行一步都要重新观测环境（如拍摄一张照片），走一步采集一步预测一步，而ACT采用的是"分块执行"策略。 具体就是累积到每K步观测一次（如K=100），然后一次性输出K个动作序列，执行这就可以按顺序执行这组K个动作序列。 动作分块也可以理解为决策频率进行了压缩，传统的单步策略需每一步观测环境并生成动作（如T次决策），而ACT是每K步观测一次，一次性生成后续K个动作序列（决策点将至T/K个），例如若K=10,1000步的任务仅需100次决策，效率提升了10倍。 将各个动作组合在一起并作为一个单元的执行，从而使起存储和执行更有效率，直观地讲一组动作可以对应抓住糖果包装纸的一角或将电池插入插槽，在实现中将块大小固定为K，每K步agent会收到一次观测然后预测生成K个动作然后机器按顺序执行。如上图所示假设K为4，t=0时刻策略观测到4个动作，然后就会生成4个动作序列，让机器按顺序执行；紧接着到t=4这个时刻，策略又观测到4个动作，生成4个预测动作机器按这个4个动作顺序执行。 分块的还可以帮助模拟人类演示中的非马尔可夫行为，具体来说是单步策略会难以应对时间相关的混杂因素，例如在采集演示过程中的停顿，会让模型这时候不知道该如何做，因为这些行为不仅仅取决于状态，还取决于时间步长，而动作分块就可以缓解当混杂因素位于一个块内是，不会引入历史条件策略的因果混淆问题。 时间集成 仅仅简单的是用动作分块实现还有一个问题，那就是每K步突然合并一个新的环境观测，可能会导致机器人运动不平稳，也就是说执行完一系列动作后，再到下一个序列动作时，可能差异比较大会导致机器抽搐。如下图中t0时刻开始执行的0~3序列切到t4时刻执行的4~7训练，这个切换过程可能会导致机器运动不平稳。 为了解决这个问题，提出了时间步查询策略。假设动作分块为K，那么每个时间刻都预测了K个序列，如上图t0时刻预测了0~3，t1时刻预测了1~4，t2时刻预测了2~5。然后每个时间刻真正要执行的序列为该时间集成加权平均，加权方案为wi = exp(−m ∗ i)，其中w0是最早的动作权重，合并新的观测速度由m控制，其中m越小表示合并越快。如上图1位置实际执行的动作为t0时刻预测的第2个动作与t1时刻预测的第1个动作加权平均，2位置实际执行的动作是t0时刻第3个预测动作、t1时刻第2个预测动作、t2时刻第1个预测动作加权平均，以此类推。靠得越紧的预测动作权重值越大，靠得远的权重值越小。 详细架构 训练 步骤1 采样数据 准备好采样数据： images：对应的4组RGB图像。 joints：2个机器，每个机器有7个自由度，那么对应14个关节位置信息。 action sequence：演示数据集长度为K组的目标动作序列，每组14个关节位置信息。 怎么理解joints和action sequence了？ 假设当前是T0时刻，采样到机器4组摄像头数据得到4 * （4806403）的图像数据，然后也采样到当前时刻机器的关节位置信息（14，）。那么action sequence数据怎么来了，要从T0时刻开始计时，到T0+K时刻进行记录K组（每组14关节位置信息）关节位置信息，然后将这些信息组合得到一组完整的数据。但一般采样的这K组数据一般使用领导臂，不使用机器的，作者在论文中提到主要是考虑因为机器是通过低级PID控制器来转换执行的，采用机器的记录数据可能会导致符合误差。 步骤2 推理Z 步骤3 预测动作 推理

模型结构 transform使用了自注意力机制，由编码器和解码器组成。 编码器 transformer的编码器输入一排向量，输出另外一排同样长度的向量。transformer的编码中加入了残差连接和层归一化，其中N X表示重复N此。首先在输入的地方需要加上位置编码，经过自注意力处理后，再嘉盛残差连接和层归一化。接下来经过全连接的前馈神经网络，再做一次残差连接和层归一化，这就是一个完整的块输出，而这个块重复N此。 上图中的块就是前面说的多头注意力+残差连接和层归一化+全连接前馈神经网络等组成。编码器可以理解为就是对输入进行编码处理。 解码器 解码器分为自回归解码和非自回归解码。 自回归解码（Autoregressive，AT） 以语言识别为例，输入一段声音，输出一串文字。 首先，将一段"机器学习"的音频输入给编码器，编码器会输出一排向量。然后将这一排向量送入到编码器中。 其次，解码器输入一个代表开始的特殊符号BOS（Begin of Sequence）,这是一个特殊的词元（token），代表开始。编码器读入BOS后，就会输出一个向量。这个向量代表了词表中每个词的概率，跟分类一样，经过了softmax操作，总和为1。向量的长度和词表一样大，每个中文一对应一个分值。 接着，在向量中挑选分数最高的作为解码器的第一个输出。这里应该就是"机"。 最后，把编码器的输出"机"当成解码器新的输入，输入为特殊符号"BOS"和"机"，解码器同样输出一个向量，这个向量里面给出了每一个中文字的分数，这里应该是"器"分数最高，这个过程反复持续下去。 上面的运作过程中，解码器把上次的输出当做输入反复下去，那么如何让解码器停止了？要让解码器停止，也需要准备一个特别的结束符号"EOS"，当产生完"习"之后，再把"习"当做编码器输入以后，解码器要能够输出"EOS"，这个EOS的概率必须最大，输出了EOS，整个解码产生的序列就结束了。 总结一下，自回归模型就是，解码器先读入编码的输入，然后输入BOS,输出W1，再把W1当做输入，再输出W2，直到输出EOS为止。 非回归解码（NAT） 自回归编码是根据上次解码器的输入一个字一个字的输出，假设要输入长度一百个字的句子，就需要做一百次的解码。那能不能一次性全部输出了？这就是非自回归解码器，假设产生的是中文的句子，非自回归不是一次产生一个字，而是一次把整个具体都产生出来。那要怎么做了，有两个做法。 方法1：用分类器来解决，将编码器的的输出结果先给分类器，分类器得到一个数字，这个数字达标的是解码器要输出的长度，比如输入是5，非自回归的解码器就是吃5个BOS，这样就产生了5个中文的子。 方法2：给编码器一堆的BOS词元，因为输出的句子有上限，假设不超过300个字，那就输入300个BOS，解码器就输出300个字，输出句子中EOS右边的输出就裁掉。 简单来说，非自回归解码是一次性输出句子，与自回归解码不同的是，非字回归解码输入的全是BOS，而自回归解码输入的是上一轮的输出。 transform的训练 既然要训练，就要去衡量误差，这个误差怎么衡量了？ 解码器的输出一个是概率分布，以输出的"机"为例，当输入"BOS"的时候，输出的答案应该要跟"机"这个向量越接近越好。 参考书籍：《深度学习详解》

运作原理 自注意力机制要解决的是让机器根据输入序列能根据上下文来理解。举个例子，输入句子为"我有一个苹果手机"，对于机器来说这里的"苹果"应该是指水果还是手机品牌了？所以要解决这个问题，就需要在上下文中去理解，那怎么在上下文中去理解了？那就是由句子中的其他词对于施加权重，让"苹果"更靠近"手机"。具体怎么做了？来看看下面的图。 上图中的a1~a4是输入的词，每个输入的词都需要跟句子中的其他词做运算得到一个输出b1~b4。如a1要得到b1，那么a1需要与a2、a3、a4输入的词进行相关运算得到b1，同理其他a2、a3、a4对应输出b2、b3、b4。注意这里a1到b1的输出并不是a1与其他a2~a4的简单相乘或相加，那具体是怎么个相关运算了？ 计算向量关联程度的方法有点积和相加，目前比较常用的是点积。下面以点积来进行说明。在自注意力模型中，采样查询-键-值（Query-Key-Value）的模式。主要分为3个步骤，分别是计算QK内积、再计算V向量、最后加权得到b。 QK内积 q： q称为查询，就是使用搜索引擎查找相关文章的关键字。q的计算方式为输入乘上Wq矩阵得到，如把a1乘上Wq得到q1。 k: k称为键值，输入乘上Wk得到向量k。如a2,a3,a4乘以Wk得到k2,k3,k4。 qk：把q和k做点积就得到a12,a13,a14，即表征a1与a2,a3,a4之间的关联性了。 通常情况下，得到最终的qk内积结果（记为axx）会进行一次归一化处理得到a'，可以使用softmax也可以使用别的激活函数，如下图所示。 最终处理的结果a'表示的是输入a1与其他a2~a4存在的关联性分数，也称为注意力分数，也可以说是一个权重值，上下文中其他的词对a1最终词的解释权重。 V向量 qk内积计算了注意力分数，那接下来需要根据注意力的分数提取出信息得到最终的b。那么要进行提取，那必然需要先获取到其他词的特征信息，怎么获取了，获取的方式非常简单，就是让各自输入乘以Wv矩阵得到一个向量V。比如a1乘以Wv得到V1,a2乘以Wv得到V2。 加权和b 得到了各自的注意力分数qk，也获取到了各自输入的特征信息，最后就可以计算最终的输出b了。公式为： $b^1 = \sum_{i} \alpha_{1,i}' v^i$ 。就是特征信息V和注意力分数进行相乘，然后把所有结果加起来。 如果a1和a2的关联性很强，那么a12'的值就大，跟V2相乘值对应也就大，这样b1的值就可能比较接近V2。所以谁的注意力分数越大，谁的V就会主导抽出的结果。 小结 上面通过以a1进行相关运算后输出b1过程，a2、a3、a4计算过程同理，同时输入的各自计算是并行的，不需要各自依赖，这也是与RNN的本质区别。同时计算过程中出现的Wq、Wk、Wv都是要学习的参数。而在实际过程中，并行运算都是通过矩阵的方式进行的，这里就不再过多阐述了。 多头注意力,所谓多头注意力，就是对应的qk有多个，也就是说W参数也有多个。 位置编码，在计算QKV的时候，引入位置编码，让输入的位置也占一定的权重。 参考书籍：《深度学习详解》

YOLOv2 回顾一下YOLOv1有哪些缺陷？ 边界框训练时回归不稳定，导致定位误差大。 每个网格只能预测两个边界框且只能识别一类目标。 小目标检测效果差。 针对以上的问题，YOLOv2进行了改进，下面从检测机制优化、网络结构优化、训练策略优化3个维度进行。 检测机制优化 锚框（Anchor Box）机制 YOLOv1每个网格只会预测一个目标，因为每个网格预测的B个边界框的类别概率都是共享的，要是有多2个目标的中心都落在了一个网格中，那么有一个目标就没法预测了。怎么解决了？ 让每个边界框都对应一个类别概率，这样就能做到每个网格可以预测多个目标了。 每个边界框训练是没有基准的，这样训练的时候就很不稳定。如果预先定义边界框，使训练的时候按照这些预定义的边界框作为基准进行训练调整。这里做个类比来理解，假设我们的目标坐标是（8，8），那么如果没有设置基准，从坐标（0,0）找到(8,8)就相对比较远，那假设我们从（6,6）这个基准开始找，那找到（8,8）的概率就大了。 上面预先定义的边界框就称为先验框（anchor Box），那么新的问题来了，这个anchor Box我们每个网格设置多少个？设置什么样的形状了？实际的数据集中Ground Truth（真实标签）边界框有些是长方形、有些是正方形。 YOLOv2使用了K均值聚类算法用于生成先验框（Anchor Boxes)，其核心目标是从训练数据中自动学习边界框的尺寸和比例，替代人工预设的锚框，从而提升检测召回率与定位精度。YOLOv2通过聚类COCO数据集，得到5个先验框尺寸（如(0.25,0.33), (0.5,0.75)...），覆盖常见物体形状。 pw，ph是先验框anchor的宽高（根据K类均值聚类得来），tx,ty,tw,th模型预测的偏移量（训练得到）。所以通过pw,ph,tx,ty,tw,th就可以计算出实际要预测的框bx,by,bw,bh。模型最终预测出tx,ty,tw,th这四个值就可以计算出bx,by,bw,bh。 这里需要注意 YOLOv2中对tx,ty进行了sigmod归一化，防止训练初期，中心点数值极大训练不稳定。 YOLOv2预测边界框的宽和高初始值是基于先验框而来，是模型对每个锚框输出宽高缩放因子（t_w, t_h)，通过聚类生成的先验框指数变换得到最终宽高。而YOLOv1是根据图像实际宽高缩放而来。 全卷积网络与先验框 YOLOv1最后阶段使用的是全连接层，使用全连接层不仅仅参数量大，同时会将先前的特征图包含的空间信息破坏，在YOLOv2中改成了全卷积结构。 可以看到输出也发生了变化YOLOv1的输出是7 x 7 x （1+4+1+4+20），而YOLOv2输出是13 x 13 x k x (1 + 4 + 20)，这里的k是每个网格的先验框数量，一般为5。（1+4+20）分别是锚框的置信度、边界框坐标、类别概率，每个anchor先验框都对应一个(1+4+20)，也就是说每个先验框可以检测一个目标，这样就解决了YOLOv1中每个网格只能检测一个目标的问题，YOLOv2中每个网格有5个先验框，就可以检测最多5个类别。 网络结构优化 加入批量归一化： YOLOv1中每层卷积都是由线性卷积+非线性激活函数组成，由于批量归一化得到越来越普遍的应用，并且效果较好，因此在YOLOv2每层卷积层都加入了批量归一化。所以卷积层就变成了线性卷积+归一化+非线性激活函数组成。 融合高分辨率特征图：YOLOv1输出的特征图是13 x 13 x 1024，分辨率越低丢失的特征就越多。为了解决这个问题，YOLOv2在第17层单独抽出一层26 x 26 x 512的特征图，然后通过特殊的降采样得到13 x 13 x 256的特征图，最后将这个13 x 13 x 256的特征图与前面13 x 13 x 1024的相加，这样达到提高特征信息保留。 多尺度训练 YOLOv2在训练上也做了进一步的优化，因为同一张图像，缩放到不同尺寸，不同尺寸包含的图像信息也不同。因此为了提高精度，引入了多尺度训练训练机制。 具体就是在训练网络时，对图像按照320、352、384、416、448、480、512、544、576、608等不同输入尺寸进行训练。 总结一下，YOLOv2针对YOLOv1的改进点有以下。 增加先验框机制：每个网格使用K类均值聚类预设K个先验框作为基准训练。每个先验框负责预测一个目标。 加入批量归一化：每个卷积层对训练数据做批量归一化处理。 高分辨率特征图：网格划分13 x 13，主干网络中抽离一路高分辨率特征图进行特殊处理然后再加回去。 对尺度训练：训练阶段使用不同尺度的图像数据进行训练。 YOLOv3 对应目标检测网络可以由主干网络、颈部网络、检测头。 主干网络：提取多尺度特征。通过卷积层、池化层等操作，将输入图像逐层抽象化，生成不同层级的特征图。有浅层特征和深层特征。浅层特征是保留细节（如边缘、纹理），适合小目标检测；深层特征是蕴含语义信息（如物体整体结构），适合大目标识别。 颈部网络：融合与优化特征。连接主干网络与检测头，整合不同层级的特征图，增强模型对不同尺度目标的感知能力。 检测头：执行具体检测任务。基于融合后的特征，输出目标的位置、类别及置信度。 YOLOv2对于小目标的检测还是不够精确，这一缺陷的主要原因是YOLOv2只使用了32倍的降采样率。 浅层卷积层：没有经过更多的卷积层处理，提出的语义信息较少，具有较浅的语义信息；但对应没有过多的降采样因此具备较多的位置信息。 深层卷积层：经过更多的卷积层处理，提取更多的语义信息；但是位置信息经过了太多的降采样，丢失了位置信息。 语义信息可以理解为是什么类别的物品，位置信息是这个物品在图中的什么坐标位置。浅层卷积层更适合检测小目标（语义信息不需要这么多），深层卷积层适合检测大目标（需要更多的语义信息）。根据这个认知，YOLOv3主干网络就使用了3个不同尺寸的特征图，分布对应的降采样是32、16、8倍。对于小尺度目标使用的是8倍将采样并在浅层网络进行先提出输出针对性处理。而大尺度目标使用32倍降采样在最深层的网络中进行输出。 输入是416 x 416的图像，输出的是3个特征图，分布是C1=B X 256 X 52 X 52；C2=B x 512 x 26 x 26;C3=B x 1024 x 13 x 13，这里的B是先验框，一般为3。针对输入图像做了52x52、26x26、13x13三种不同疏密度的网格。 3个特征图根据多级检测结构推理后，得到最终预测的3个结果。y1= B x (4 + 1 + Nc) x 13 x 13;y2= B x (4 + 1 + Nc) x26 x 26;y3= B x (4 + 1 + Nc) x 52 x 52; 其中B为先验框数量，一般是3。Nc是类别个数，根据实际数据集，YOLOv3使用的是COCO数据集，有80个类别。 参考： 书籍《YOLO目标检测》

介绍 YOLO在目标视觉检测应用广泛，You Only Look Once的简称。作者期望YOLO能像人一样只需要看一眼就能够立即识别其中的物体、位置及交互关系。能够达到快速、实时检测的效果。 YOLO检测系统可以简要分为3个步骤： Resize image：调整输入图像的大小为448 x 448。 Run Convolutional network:CNN卷积网络处理。 Non-max suppression:使用非极大值抑制。 YOLO与其他目标检测系统有什么不同或优势？ YOLO 非常简单，如上图。单个卷积网络可以同时预测多个边界框及其类别概率。YOLO 使用完整图像进行训练，并直接优化检测性能。与传统的目标检测方法相比，这种统一的模型具有诸多优势。 首先，YOLO速度极快。由于YOLO将检测视为一个回归问题，因此无需复杂的流程。只需在测试时对一张新图像运行神经网络即可预测检测结果。 其次，YOLO在进行预测时会全局推理图像。与滑动窗口和基于区域提议的技术不同，YOLO在训练和测试期间会查看整幅图像，因此它隐式地编码了关于类别及其外观的上下文信息。Fast R-CNN 是一种领先的检测方法，由于无法看到更大的背景，它会将图像中的背景块误认为是物体。与 Fast R-CNN相比，YOLO 的背景错误率不到一半。 最后，YOLO学习的是可泛化的对象表征。在使用自然图像进行训练并在艺术作品上进行测试时，YOLO 的表现远超DPM和R-CNN 等领先的检测方法。由于 YOLO 具有高度的泛化能力，因此在应用于新领域或意外输入时，它不太可能崩溃。 更为详细的结构如下： 该网络包含24个卷积层和2个全连接层。不同于GoogLeNet使用的Inception模块，我们采用1×1降维层接3×3卷积层的简单设计。输入是448 x 448 x 3张量，最终输出是7×7×30的预测张量。 检测原理 YOLO是做统一检测，其网络使用整幅图像的特征来预测每个边界框。它还能同时预测图像所有类别的所有边界框。这意味着YOLO网络对整幅图像及其中的所有物体进行全局推理。 划分网格： 将输入图像划分为S X S个网格（grid）。 预测边界框：每个网格预测B个边界框（包含4个预测值x、y、w、h）并计算这些边界框的置信度分数以及C个条件类别概率。 置信度分数计算方式为：当网格中不存在任何物体，则为0，如果存在则等于预测框与真实框的交并比IOU。 C个条件类别概率：是C个预测类别，每个类别的概率值。因此总结一下，预测值为S X S X (B X 5 + C)个tensor。这里要注意的是，边界框的中心点并不是网格中心点，但中心点落在的这个网格负责这B个边界框的预测。 上面的图出之YOLOv1论文中的第5版本，如果不是很直观可以看看第1个版本，只不过第一个版本每个网格只预测一个边界框并且没有包含置信度。 为什么YOLOv1改进加了一个置信度？ 预测框与真实框的交并比（定位质量），这样可以预测质量。YOLO将图像划分为网格，每个网格仅预测一组类别概率（与预测框数量无关），若直接用类别概率判断物体存在性，会忽略定位质量。例如一个网格预测出“狗”的概率为90%，但预测框可能严重偏离真实物体（IoU低），此时置信度会因低IoU而降低，避免高类别概率但定位差的误检。 为什么YOLOv1最开始每个网格是一个边界框后面变成了多个？ 单框局限：每个网格仅预测一个边界框时，模型难以适应不同长宽比的物体（如瘦高的行人和扁平的汽车）。 多框设计：通过预测两个不同长宽比的边界框（如一个方形、一个长方形），模型可灵活匹配不同形状的目标，提高定位精度。 训练机制：训练时，选择与真实框IoU更高的预测框负责该物体，另一个框则被抑制（不参与损失计算），从而驱动网络学习多样化的边界框表达。 单框瓶颈：网格内若存在多个重叠目标（如密集人群），单框设计只能检测其中一个物体，导致漏检49。 冗余预测：两个边界框提供双重检测机会，即使一个框被错误抑制，另一框仍可能捕获未被覆盖的目标811。 但是这里需要注意的是，在YOLOv1中，同一个网格内的两个边界框（边界框1和边界框2）预测的类别结果是同一个类，因为类别的预测是共享的，也就是说预测的类别概率是共享的，每个网格只能预测一个类别目标。这也是YOLOv1的缺陷，如果有2个不同类别的物体中心都落在了同一个网格中，这样就没有同时预测两个物体。 总结：YOLO系统将检测建模为回归问题，它将图像划分为 S × S 的网格，并为每个网格单元预测 B 个边界框、这些框的置信度以及 C 个类别概率。这些预测被编码为S × S × (B ∗ 5 + C) 张量。为了在 PASCAL VOC 上评估 YOLO，作者使用 S = 7，B = 2。PASCAL VOC 有 20 个标记类别，因此 C = 20，最终预测是一个结果是7 × 7 × 30的张量。 损失函数 YOLOv1的损失函数使用的是边界框坐标（x,y,w,h）、置信度、类别概率计算而来，公式如下图。 边界框坐标损失：第一第二行公式，计算的是边界框坐标的损失。 置信度损失：分为有目标和无目标，无目标学习标签就是0，有目标学习标签是1. 类别损失：每个类别的损失，针对的是每个网格单元的损失，不是预测框的。 关于边界框的位置参数是怎么样的？下面总结一下： tx, ty： 是边界框中心坐标相对于当前网格（第5行第二列）左上角的偏移量（归一化到 [0,1] 区间）。 w, h: 是边界框的实际宽度和高度归一化到 [0,1]，相对于整张图像的尺寸宽和高进行进行缩小比例。 详细的计算公式： 中心点坐标：x = (C_x + tx) / S, y = (C_y + ty) / S，（C_x, C_y为网格左上角坐标，S为网格划分数量） 宽高：w = 框宽 / 图宽, h = 框高 / 图高 YOLOv1的边界框参数优点是直接预测实际位置，无需先验框（Anchor Box），模型结构简单。缺点就宽高直接回归导致训练不稳定，定位精度较低； 模型后处理 YOLOv1模型训练完成后，给定一个448 x 448 x 3的tensor，模型输出是一个7 x 7 x 30的 tensor，也就是每个网格位置包含2个边界框的置信度输出C1和C2，两个边界框的位置参数（tx1,ty1,w1,h1）和（tx2,ty2,w2,h2）以及20个类别的概率p1~p20。 显然上面的输出结果不是我们想要的，我们要进行处理，筛选出最优的值，具体的处理步骤如下： 计算所有边界框得分：每个网格预测的边界框进行计算得分，计算公式分数=置信度值 x 类别概率中最大的值。 阈值剔除： 根据上一个步骤计算的得分，设定一个阈值比如0.3， 剔除小于阈值分数的边界框。 计算边界框位置：剔除一部分阈值后，计算编辑框的参数位置包括x,y,w,h。 非极大值抑制：经过前面的步骤后，同一个目标可能还是有多个预测边界框，最后试用非极大值抑制将重复检查的框去掉。最后就得到下面的示例结果。 总结一下YOLOv1的优缺点： 优点： 速度快，实时性强：首次实现端到端训练，推理速度达 45 FPS，简化了检测流程。 结构简单： 统一为单一回归问题，避免了区域提议（Region Proposal）的复杂步骤。 计算效率高：全卷积网络设计，适合资源受限的嵌入式设备。 缺点： 检测精度低：每个网格仅预测2个边界框且只能识别单一物体，同时对密集小目标检测效果差网络划分7x7精度不够。 定位不准确：边界框回归不稳定，导致定位误差大，与边界框的宽高定义为实际宽高缩放有关。 灵活性差：输入分辨率固定（448×448），不支持多尺度训练，网格划分（如 7×7）限制检测数量上限（最多 49 个物体）。 泛化能力弱：对非常规长宽比或重叠物体处理效果差。 参考： 1. 论文：https://arxiv.org/pdf/1506.02640v5 2. 书籍《YOLO目标检测》