从数学角度理解flow matching中的线性插值

什么是插值

插值的核心问题是：在已知两个点的情况下，如何找到它们之间的中间点。

举个人走路的例子，起点在家门口(A点)，终点在公司(B点)，总的路程为1000米，假设人是匀速移动，如果走到一半(t=0.5)，那么人就在家和公司的正中间，如果走到四分之一(t=0.25)，那么离家250米，离公司750米。

线性插值（LERP） 是最简单的一种：它假设两个点之间的变化是“直线型、匀速”的。

---

公式

x_t = (1-t)x_0 + t x_1, \quad t \in [0,1]

把两个量x_0和x_1按加权1-t与t做加权平均，得到他们之间的线性过渡点。x_0是起点，x_1是终点，t是插值因子，控制起点与重点的位置。当 t=0，结果是 x_0；当 t=1，结果是 x_1；当 t=0.5，结果是中点；t从0到1连续变化时，x_t沿着二者之间等速变化（为什么是等速，待会解释）。

先上个图看看直观体会一下。

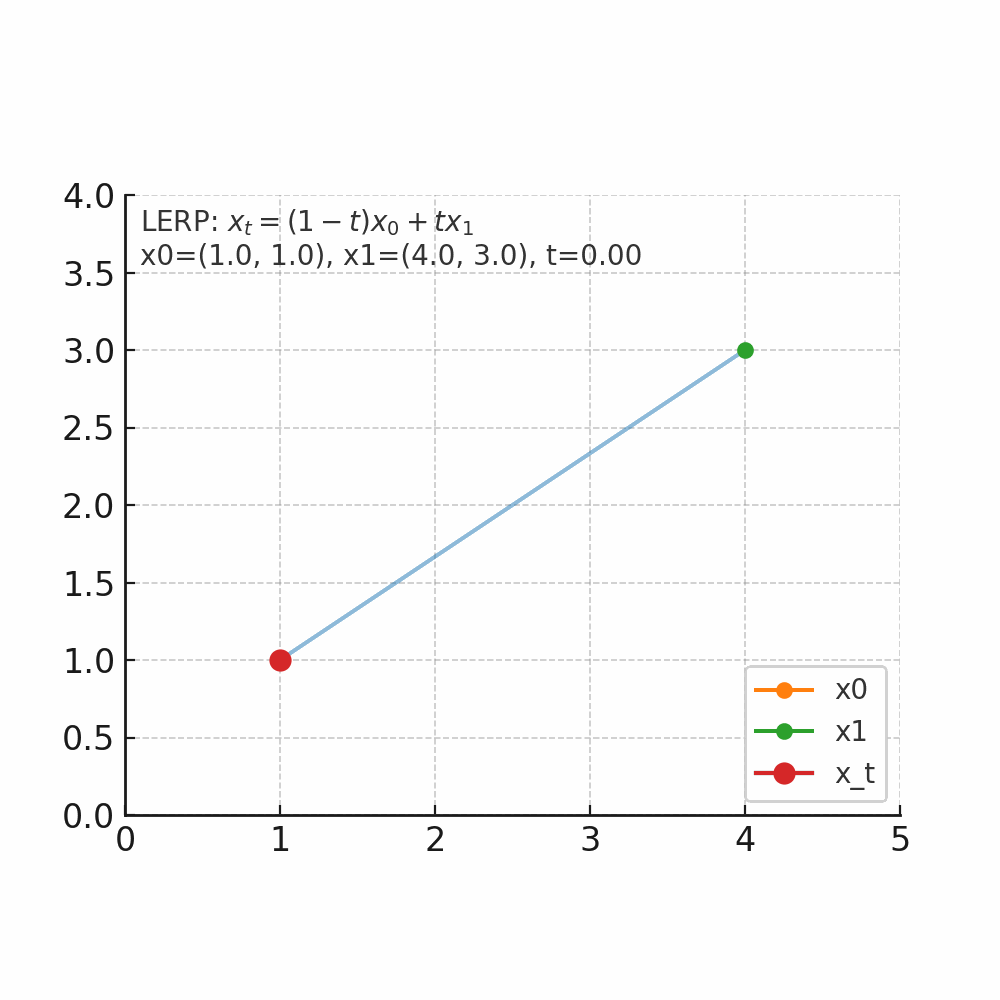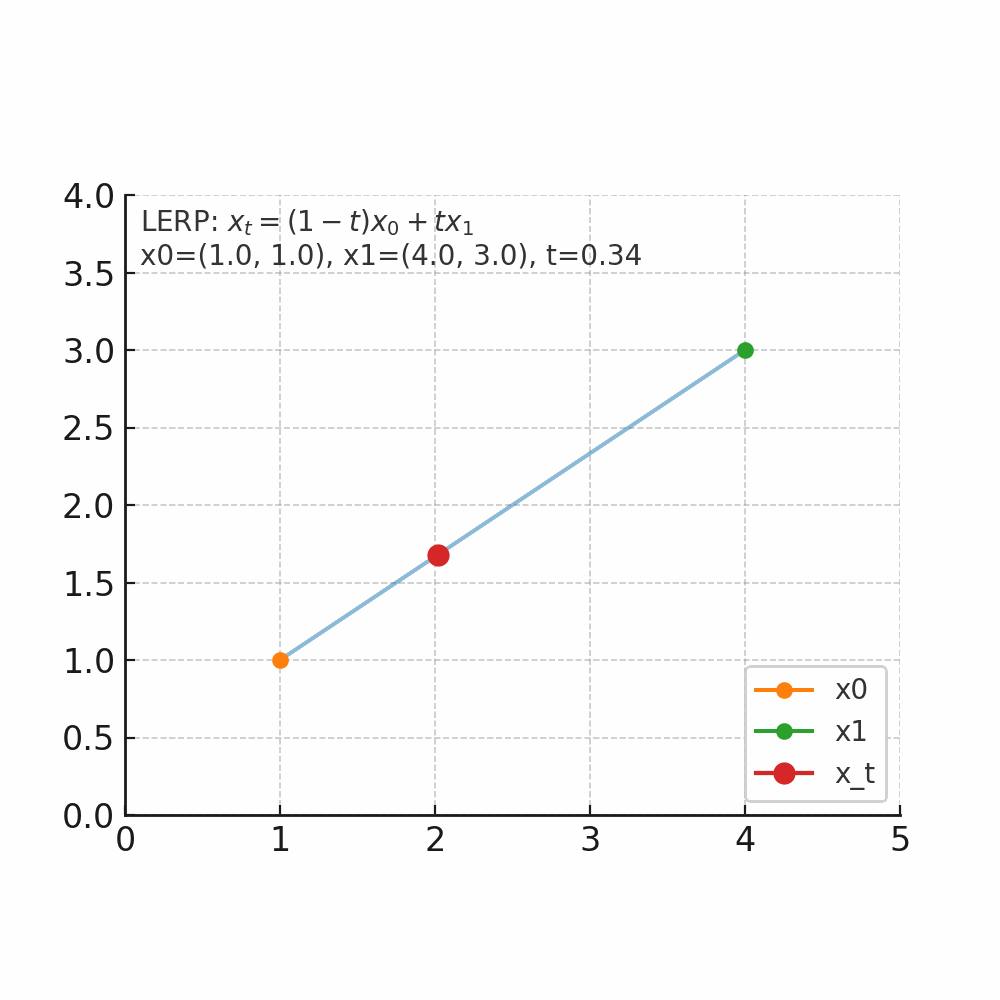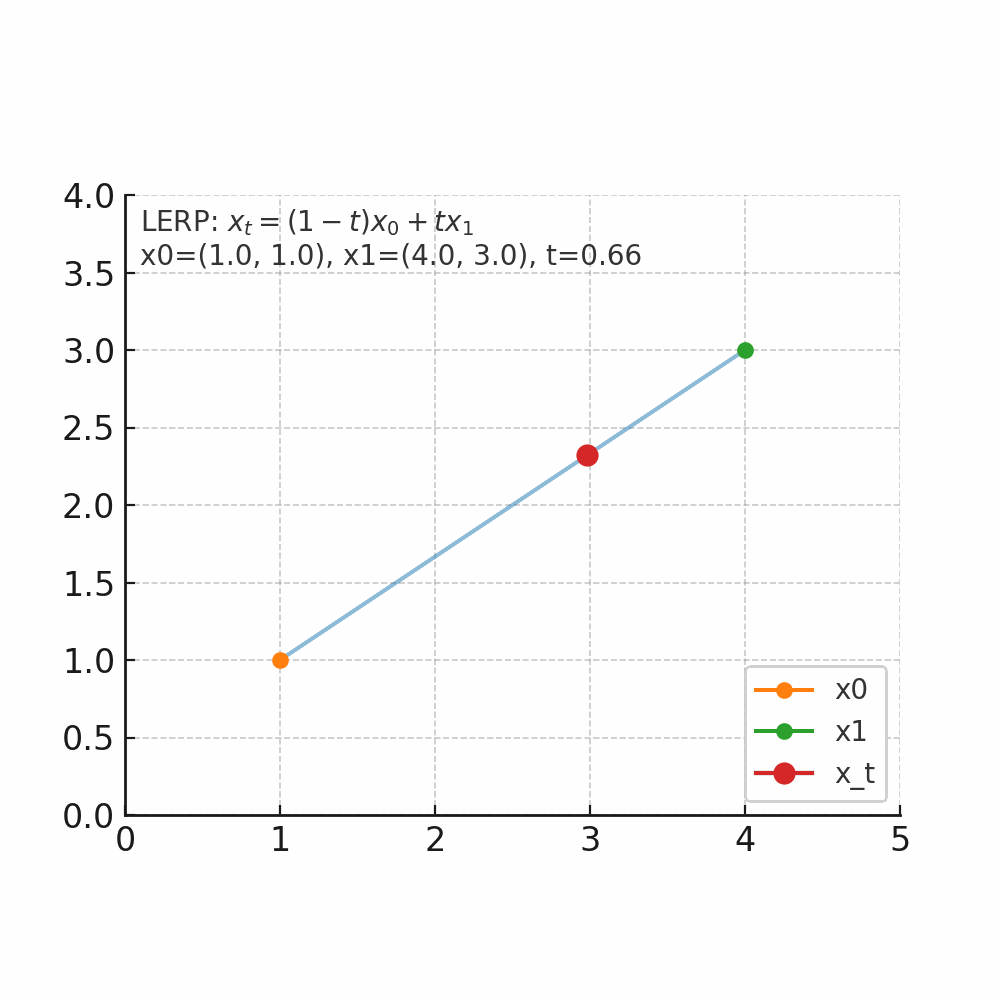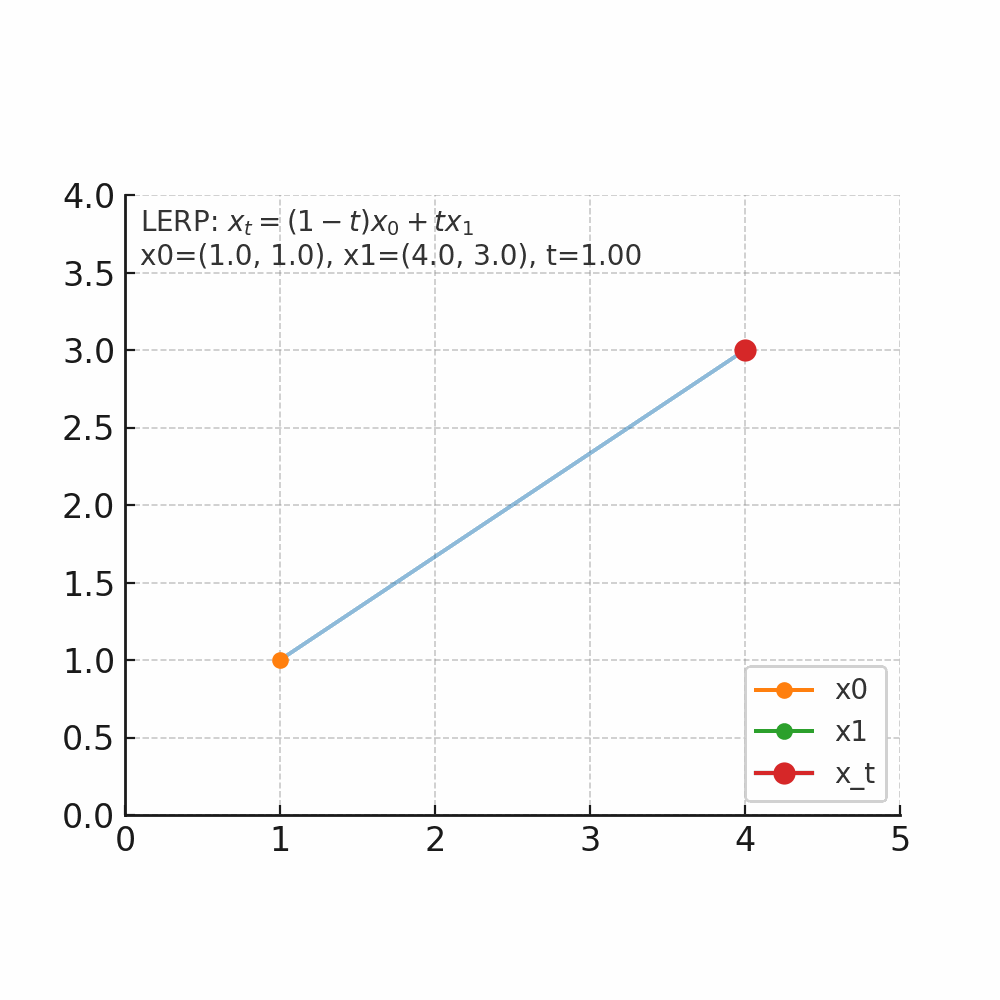
如图所示起点x_0为坐标（1，1），终点x_1（4，3），当t从0开始连续变化是，x_t的位置会朝着x_1的方向变化。

• 当t=0时，坐标为(1 – 0) x (1, 1) + 0 x (4, 3) = (1, 1)。
• 当t=0.2时，坐标为(1 – 0.2) x (1, 1) + 0.2 x (4, 3) = (1.6, 1.4)。
• 当t=0.5时，坐标为(1 – 0.5) x (1, 1) + 0.5 x (4, 3) = (2.5, 2)。
• 当t=1时，坐标为(1 – 01) x (1, 1) + 1 x (4, 3) = (4, 3)。

通过公式可以算出每个时间的位置，但是如果要知道每个位置变化的速度/趋势我们应该怎么来衡量了？

那自然就是要求导数了。

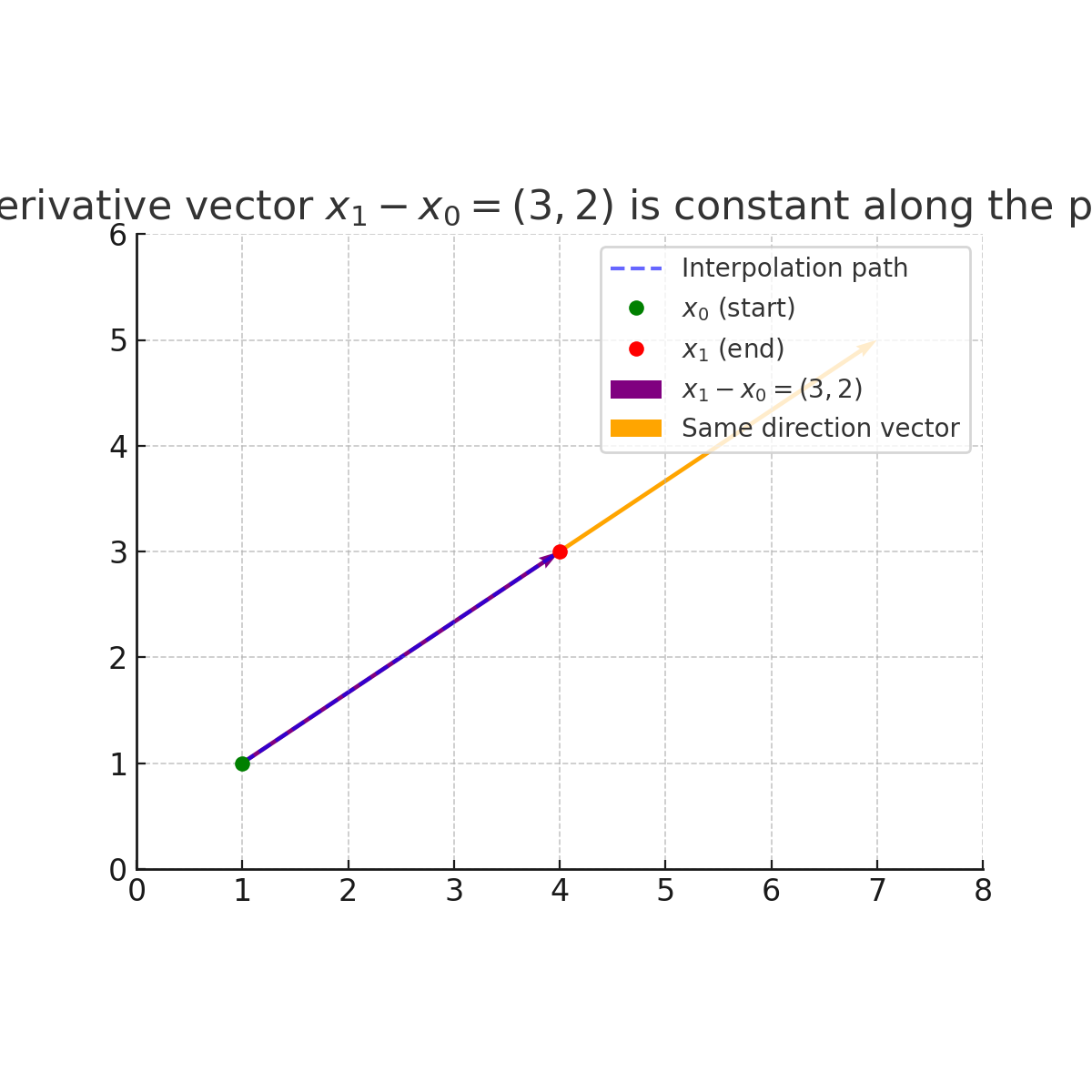
\frac{d}{dt}x_t = x_1 – x_0

可以看到其倒数是一个常数，那就意味着变化是匀速的，以上图为例，都是朝着(4,3)-(1,1)=(3,2)的向量方向去变化。

有了这个变化量，假设我们时间步\Delta t=0.1，那么意味着每次变化的位置是0.1 x (3,2) = (0.3, 0.2)；假设当前位置是(1,1)那么就可以计算出下一个时间步的位置为(1,1)+(0.3,0.2)=(1.3,0.2)。这就与我们此前flow matching里面的公式x_{k+1} = x_k + v_\theta(x_k, t_k)\Delta t。