GGML的CPU算子解读:矩阵乘法
算子实现
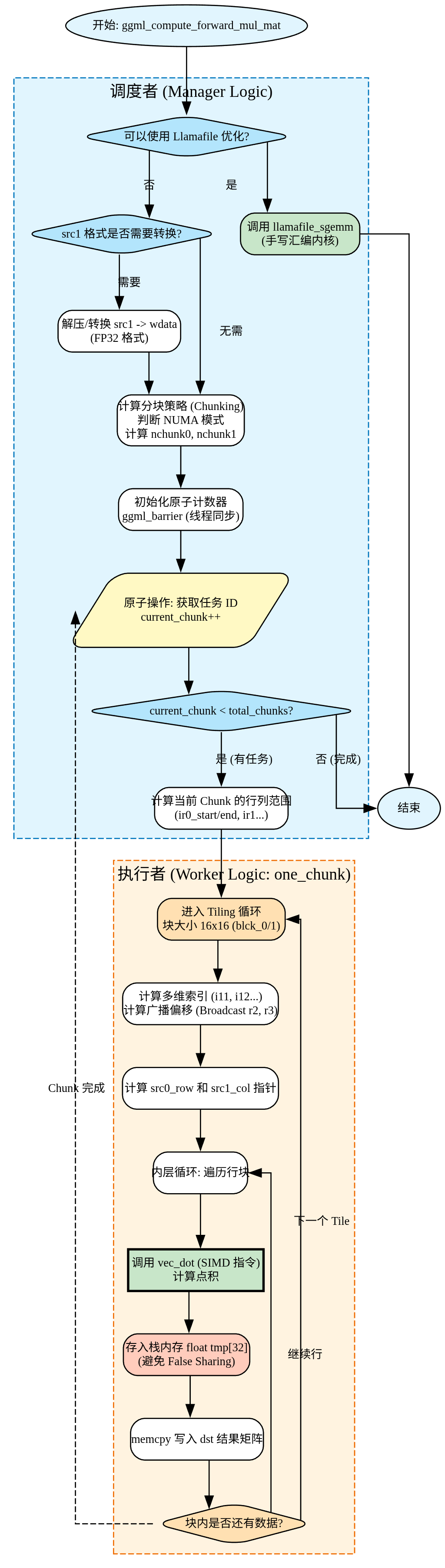
调用流程
主要是ggml_compute_forward_mul_mat函数,该函数把任务拆分,最终计算执行调用ggml_compute_forward_mul_mat_one_chunk实现。
任务拆分
void ggml_compute_forward_mul_mat(
const struct ggml_compute_params * params,
struct ggml_tensor * dst) {
// 1. 获取输入和输出张量的指针
const struct ggml_tensor * src0 = dst->src[0];
const struct ggml_tensor * src1 = dst->src[1];
// 2. 初始化一堆本地变量 (ne0, nb0 等),方便后面写公式
GGML_TENSOR_BINARY_OP_LOCALS
// 3. 获取当前线程的信息
const int ith = params->ith; // 我是第几个线程?
const int nth = params->nth; // 总共有几个线程?
// 4. 获取src0(权重)的数据类型,用于后续查询src1(输入/激活值)必须转换为什么类型才能进行计算。
//在大语言模型中,为了省内存,src0(权重矩阵)通常是经过量化的比如Q4_0,Q5_1,Q8_0等格式。
enum ggml_type const vec_dot_type = type_traits_cpu[src0->type].vec_dot_type;
// ... (省略一堆 GGML_ASSERT 检查,确保维度合法,比如 src0 和 src1 能不能相乘) ...
#if GGML_USE_LLAMAFILE
// 5. 【极速通道】如果系统支持 llamafile 的手写汇编优化,直接丢给它算,算完直接返回。
// 这比下面的 C 代码快得多。
if (src1_cont) {
// ... 尝试调用 llamafile_sgemm ...
if (!llamafile_sgemm(...)) goto UseGgmlGemm1; // 如果失败,就跳回下面的普通通道
return;
}
UseGgmlGemm1:;
#endif
// 6. 如果src1的类型与src0的类型不匹配,需要将src1转换成vec_dot_type类型。
if (src1->type != vec_dot_type) {
char * wdata = params->wdata;
// ... (循环遍历 src1,把数据解压并复制到 wdata) ...
// 这里用了 from_float 函数进行转换
}
// 7. 【同步】确保所有线程都知道数据准备好了
//只让线程0做一次初始化,把 current_chunk 设为 nth:因为每个线程先从 current_chunk = ith
//开始领一个“私有起始 chunk”,所以下一个“公共可抢”的 chunk 从 nth 开始。
if (ith == 0) {
atomic_store_explicit(¶ms->threadpool->current_chunk, nth, memory_order_relaxed);
}
ggml_barrier(params->threadpool);
// barrier 等待:确保所有线程都完成了“src1 预处理/计数器初始化”,再进入真正的 chunk 计算阶段。
// ... (再次尝试 llamafile 优化,省略) ...
// 8. 【切蛋糕】决定每个任务块 (chunk) 有多大
// nr0 是结果矩阵的行数,nr1 是其余维度的大小
const int64_t nr0 = ne0; //nr0 代表结果矩阵在“第一维”的长度(可以理解为输出的行数/一个主维度)。
const int64_t nr1 = ne1 * ne2 * ne3;
//nr1 把其余维度展平成第二维(把 ne1*ne2*ne3 看成“列块/批次展平后的列方向”)。
int chunk_size = 16; // 默认每块按 16 规模做分块(和 one_chunk 内的 16×16 tiling 呼应)。
if (nr0 == 1 || nr1 == 1) { chunk_size = 64; } // 如果矩阵很细长,就切大一点
// 算出总共有多少块蛋糕 (nchunk0 * nchunk1)
int64_t nchunk0 = (nr0 + chunk_size - 1) / chunk_size;
int64_t nchunk1 = (nr1 + chunk_size - 1) / chunk_size;
// 9. 【NUMA 优化】如果是多路 CPU 服务器,或者切得太碎了,就改用保守策略
if (nchunk0 * nchunk1 < nth * 4 || ggml_is_numa()) {
nchunk0 = nr0 > nr1 ? nth : 1;
nchunk1 = nr0 > nr1 ? 1 : nth;
}
// 计算每个块实际包含多少行/列 (dr0, dr1)
//把 nr0/nr1 平均分给 nchunk0/nchunk1,得到每块在两维上的跨度 dr0/dr1。
const int64_t dr0 = (nr0 + nchunk0 - 1) / nchunk0;
const int64_t dr1 = (nr1 + nchunk1 - 1) / nchunk1;
// 10. 【开始干活】线程开始领任务
// 一开始,第 ith 个线程领第 ith 块蛋糕
//每个线程先从 current_chunk = ith 开始,保证一开始每个线程都有活(减少原子争用)。
int current_chunk = ith;
while (current_chunk < nchunk0 * nchunk1) {
// 算出当前蛋糕块在矩阵的哪个位置 (start 到 end)
const int64_t ith0 = current_chunk % nchunk0;
const int64_t ith1 = current_chunk / nchunk0;
const int64_t ir0_start = dr0 * ith0;
const int64_t ir0_end = MIN(ir0_start + dr0, nr0);
// ... (同理算出 ir1 的范围) ...
// 11. 【核心调用】把这一小块任务交给工人去算
// num_rows_per_vec_dot 是看 CPU 是否支持一次算两行 (MMLA 指令)
ggml_compute_forward_mul_mat_one_chunk(..., ir0_start, ir0_end, ir1_start, ir1_end);
// 如果线程数比蛋糕块还多,干完这一块就可以下班了
if (nth >= nchunk0 * nchunk1) { break; }
// 12. 【抢任务】否则,去原子计数器里“取号”,领下一块没人干的蛋糕
current_chunk = atomic_fetch_add_explicit(¶ms->threadpool->current_chunk, 1, memory_order_relaxed);
}
}
计算执行
static void ggml_compute_forward_mul_mat_one_chunk(
// ... 参数省略,主要是范围 ir0_start 等 ...
) {
// 1. 获取数据指针
const struct ggml_tensor * src0 = dst->src[0];
const struct ggml_tensor * src1 = dst->src[1];
// ... 初始化本地变量 ...
// 2. 准备点积函数 (vec_dot)
// type_traits_cpu 是一张表,根据数据类型查到最优的计算函数
ggml_vec_dot_t const vec_dot = type_traits_cpu[type].vec_dot;
// 3. 【广播因子】计算 src1 比 src0 大多少倍
// 比如 src1 有 2 个头,src0 只有 1 个头,那 r2 就是 2。计算时 src0 要重复用。
const int64_t r2 = ne12 / ne02;
const int64_t r3 = ne13 / ne03;
// 如果任务范围是空的,直接返回
if (ir0_start >= ir0_end || ir1_start >= ir1_end) { return; }
// 4. 【Tiling 分块参数】
// 即使是这一小块任务,也要再切碎,为了放进 CPU 缓存 (L1 Cache)
const int64_t blck_0 = 16;
const int64_t blck_1 = 16;
// 5. 定义临时缓冲区,防止多个线程写内存冲突 (False Sharing)
float tmp[32];
// 6. 【双重 Tiling 循环】开始遍历任务块
// iir1 每次跳 16 行
for (int64_t iir1 = ir1_start; iir1 < ir1_end; iir1 += blck_1) {
// iir0 每次跳 16 列
for (int64_t iir0 = ir0_start; iir0 < ir0_end; iir0 += blck_0) {
// 7. 【处理块内的每一行】
for (int64_t ir1 = iir1; ir1 < iir1 + blck_1 && ir1 < ir1_end; ir1 += num_rows_per_vec_dot) {
// 8. 【计算索引】这部分数学很绕,简单说就是:
// 根据当前的行号 ir1,反推出它在 src1 的第几层、第几页 (i13, i12, i11)
const int64_t i13 = (ir1 / (ne12 * ne1));
const int64_t i12 = (ir1 - i13 * ne12 * ne1) / ne1;
const int64_t i11 = (ir1 - i13 * ne12 * ne1 - i12 * ne1);
// 9. 【应用广播】算出对应的 src0 的位置
// 如果 src0 比较小,就除以倍率 r2, r3 来复用数据
const int64_t i03 = i13 / r3;
const int64_t i02 = i12 / r2;
// 拿到 src0 这一行的内存地址
const char * src0_row = (const char*)src0->data + (0 + i02 * nb02 + i03 * nb03);
// 拿到 src1 这一列的内存地址 (wdata 是之前解压好的数据)
const char * src1_col = (const char*)wdata + ...; // (省略复杂的偏移量计算)
// 拿到 结果 dst 的写入地址
float * dst_col = (float*)((char*)dst->data + ...);
// 10. 【核心计算循环】
// 遍历 src0 的行 (分块内),调用 SIMD 指令进行计算
for (int64_t ir0 = iir0; ir0 < iir0 + blck_0 && ir0 < ir0_end; ir0 += num_rows_per_vec_dot) {
// vec_dot:一次性计算 ne00 个元素的点积
// 结果先存在 tmp 数组里,而不是直接写回 dst
vec_dot(ne00, &tmp[ir0 - iir0], ..., src0_row + ir0 * nb01, ..., src1_col, ...);
}
// 11. 【写回结果】
// 把算好的 tmp 里的数据,一次性拷贝 (memcpy) 到最终的目标 dst_col
for (int cn = 0; cn < num_rows_per_vec_dot; ++cn) {
memcpy(&dst_col[iir0 + ...], tmp + ..., ...);
}
}
}
}
}
以一个例子来总结一下。
void ggml_compute_forward_mul_mat(
const struct ggml_compute_params * params, // 计算参数(包含线程信息)
struct ggml_tensor * dst // 结果矩阵 C = A × B
)
功能是矩阵乘法:结果矩阵C=矩阵A x 矩阵B。其并行的策略如下:
- 切分对象: 结果矩阵C(不是A和B)
- 并行方式:2D切分+work_stealing(工作窃取)
- 写入方式:每个线程直接写入结果矩阵的不同位置。
矩阵A (m×k) × 矩阵B (k×n) = 结果矩阵C (m×n)
↑ ↑ ↑
只读 只读 切分这个!
如上,矩阵A和B是只读的,所有线程都需要读取完整的A和B,结果矩阵C需要写入,每个线程写入不同的位置,切分C可以让多个线程并行计算不同的部分,互不干扰。
示例演示
输入数据
矩阵A (4行×3列):
┌─────────┐
│ 1 2 3 │
│ 4 5 6 │
│ 7 8 9 │
│ 10 11 12│
└─────────┘
矩阵B (3行×4列):
┌─────────────┐
│ 1 2 3 4 │
│ 5 6 7 8 │
│ 9 10 11 12 │
└─────────────┘
要计算:结果矩阵C = A × B (4行×4列)
分配结果矩阵
结果矩阵C(内存已分配,4×4 = 16个float):
┌─────────────────────┐
│ ? ? ? ? │ ← 行0
│ ? ? ? ? │ ← 行1
│ ? ? ? ? │ ← 行2
│ ? ? ? ? │ ← 行3
└─────────────────────┘
列0 列1 列2 列3
计算切分参数
假设:2个线程,chunk_size = 2
nr0 = 4, nr1 = 4
nchunk0 = (4 + 2 - 1) / 2 = 3
nchunk1 = (4 + 2 - 1) / 2 = 3
总块数 = 3 × 3 = 9
检查:9 < 2 * 4 = 8? 不,9 >= 8
-> 不触发优化,保持3×3切分
dr0 = (4 + 3 - 1) / 3 = 2 // 每个块2行
dr1 = (4 + 3 - 1) / 3 = 2 // 每个块2列
切分结果矩阵
结果矩阵C (4×4) 被切分成9个块:
┌──────┬──────┬──────┐
│ 块0 │ 块1 │ 块2 │ ← 行块0(行0-1)
│[0,0] │[0,1] │[0,2] │
│[1,0] │[1,1] │[1,2] │
├──────┼──────┼──────┤
│ 块3 │ 块4 │ 块5 │ ← 行块1(行2-3)
│[2,0] │[2,1] │[2,2] │
│[3,0] │[3,1] │[3,2] │
├──────┼──────┼──────┤
│ 块6 │ 块7 │ 块8 │ ← 行块2(超出边界)
│[0,3] │[1,3] │[2,3] │
│[1,3] │[2,3] │[3,3] │
└──────┴──────┴──────┘
映射表
列0 列1 列2 列3
┌────┬────┬────┬────┐
│块0 │块0 │块3 │块3 │ ← 行0
│ │ │ │ │
├────┼────┼────┼────┤
│块0 │块0 │块3 │块3 │ ← 行1
│ │ │ │ │
├────┼────┼────┼────┤
│块1 │块1 │块4 │块4 │ ← 行2
│ │ │ │ │
├────┼────┼────┼────┤
│块1 │块1 │块4 │块4 │ ← 行3
└────┴────┴────┴────┘
块0: ith0=0, ith1=0 → C[0:2, 0:2] → 左上角 2×2
块1: ith0=1, ith1=0 → C[2:4, 0:2] → 左下角 2×2
块3: ith0=0, ith1=1 → C[0:2, 2:4] → 右上角 2×2
块4: ith0=1, ith1=1 → C[2:4, 2:4] → 右下角 2×2
转换的过程
// 步骤1:块编号 → 块坐标
current_chunk = 3
ith0 = 3 % 3 = 0 // 块在第0行(行方向的第0个块)
ith1 = 3 / 3 = 1 // 块在第1列(列方向的第1个块)
// 步骤2:块坐标 → 实际位置
ir0_start = dr0 * ith0 = 2 * 0 = 0 // 从第0行开始
ir0_end = MIN(0 + 2, 4) = 2 // 到第2行结束(不包括2,实际是0-1行)
ir1_start = dr1 * ith1 = 2 * 1 = 2 // 从第2列开始
ir1_end = MIN(2 + 2, 4) = 4 // 到第4列结束(不包括4,实际是2-3列)
// 步骤3:实际位置 → 结果矩阵元素
块3 = C[0:2, 2:4] = {
C[0][2], C[0][3],
C[1][2], C[1][3]
}
之所以要做一个映射,是因为work-stealing需要一维的变化,原子操作只能操作一个整数,线程并发是以块为最小运算单位。也是为了方便后面做负载均衡。
并行运算
(1)线程0的工作
current_chunk = 0 // 从块0开始
// 处理块0
ith0 = 0 % 3 = 0, ith1 = 0 / 3 = 0
ir0_start = 0, ir0_end = 2 // 行0-1
ir1_start = 0, ir1_end = 2 // 列0-1
计算:
C[0][0] = A[0行] · B[第0列] = [1,2,3]·[1,5,9] = 38
C[0][1] = A[0行] · B[第1列] = [1,2,3]·[2,6,10] = 44
C[1][0] = A[1行] · B[第0列] = [4,5,6]·[1,5,9] = 83
C[1][1] = A[1行] · B[第1列] = [4,5,6]·[2,6,10] = 98
直接写入结果矩阵:
dst->data[0*4 + 0] = 38 // C[0][0]
dst->data[0*4 + 1] = 44 // C[0][1]
dst->data[1*4 + 0] = 83 // C[1][0]
dst->data[1*4 + 1] = 98 // C[1][1]
// 完成后,抢下一个块
current_chunk = atomic_fetch_add(¤t_chunk, 1) = 2
// 处理块2(无效,会被跳过)
ir0_start = 4, ir0_end = 4 // 空
→ 跳过
// 继续抢下一个块
current_chunk = atomic_fetch_add(¤t_chunk, 1) = 3
// 处理块3
(2)线程1的工作
current_chunk = 1 // 从块1开始
// 处理块1
ith0 = 1 % 3 = 1, ith1 = 1 / 3 = 0
ir0_start = 2, ir0_end = 4 // 行2-3
ir1_start = 0, ir1_end = 2 // 列0-1
计算并写入 C[2:4, 0:2]...
// 完成后,抢下一个块
current_chunk = atomic_fetch_add(¤t_chunk, 1) = 4
// 处理块4
(3)最终的结果
所有线程完成后,结果矩阵C:
┌─────────────────────┐
│ 38 44 50 56 │ ← 所有元素都已计算并写入
│ 83 98 113 128 │
│ 128 152 176 200 │
│ 173 206 239 272 │
└─────────────────────┘