最新文章
-
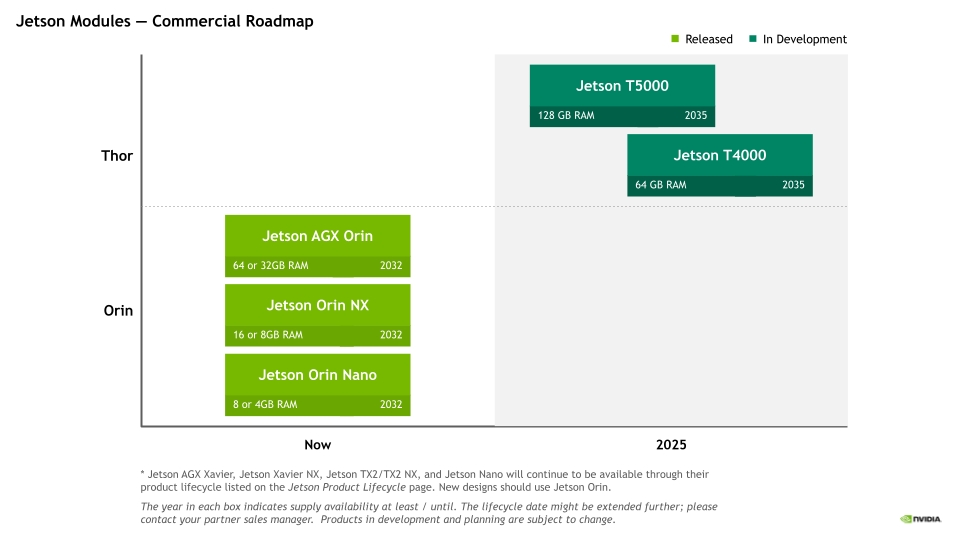
NVIDIA Jetson平台简介:机器人和边缘AI
简介 NVIDIA Jetson平台提供用于开发和部署AI赋能机器人、无人机、IVA(Intelligent Video Analytics,智能视频)应用和自主机器的工具。在边缘生成式AI、NVIDIA Metropolis和Isaac平台支持下,Jetson提供可拓展得软件、现代AI堆栈、灵活的微服务和API、生成就绪型ROS软件包以及特定于应用程序的AI工作流。 Jetson 硬件Roadmap,分为商业方向和工业方向。 上图是商业硬件roadmap,主要分为orin(欧林)和thor(雷神)两个系列。 而工业方向roadmap主要是entry、mainstream、perfromance三个方向。 在软件方面,jetson提供JetPack软件包,截止目前最新的发布版本是JetPack 7.0,主要是基于ubuntu 24.04,集成了CUDA 13.0以及holoscan sensor bride支持。 硬件 NVIDIA Jetson 模组可提供适合各种性能水平和价位的加速计算功能,从而能够满足各种自主应用的需求。从制造业到建筑业,从医疗健康到物流行业,Jetson 平台都能提供出色的性能、卓越的能效和无比轻松的开发体验。下面是jetson系列提供的模组规格简要对比。 上面是NVIDIAjetson系列的模组从最小0.5TFLOPS算力到最大2070 TOPS算力的平台矩阵。 Nano:四核A57@1.43G CPU+128核Maxwell架构GPU+4GB LPDDR内存,可提供472 FGLOP的AI算力;并行运行多个神经网络并同时处理多个高分辨率传感器,其功耗仅需5~10W;应用在网络硬盘录像机(NVR)、家用机器人以及具备全面分析功能的智能网关上面。 TX2:双核NVIDIA Denver™@1.95G+四核Arm® Cortex®-A57@1.92G CPU+256核 Pascal GPU+4GB/8GB LPDDR内存,可提供1.3TFLOPS的AI算力;计算性能翻倍,功耗仅7.5W。可应用在工厂机器人、商用无人机、便携式医疗设备和企业协作设备中。 Xavier NX:6核NVIDIA Carmel ARM®v8.2 64 位 CPU + 48 个 Tensor Core 的 384 核 NVIDIA Volta™ GPU+8/16GB LPDDR4x内存;可提供14TOPS+功耗10W~21TOPS+功耗20W的AI算力;应用在 适用于无人机、便携式医疗设备、小型商业机器人、智能摄像头、高分辨率传感器、自动光学检测、智能工厂和其他 IoT 嵌入式系统等高性能 AI 系统。 AGX Xavier:8 核 NVIDIA Carmel Armv8.2 64 位 CPU+512 个 NVIDIA CUDA Core 和 64 个 Tensor Core Volta 架构GPU+32/64GB内存,提供32TOPS的AI算力,功耗在10W~40W;非常适用于配送和物流机器人、工厂系统和大型工业UAV等自主机器。 Orin Nano、NX、AGX:6\~12核 Arm® Cortex® A78AE v8.2@1.7G\~2.2G +(32\~64)x (1024\~2048)核Ampere 架构 GPU+4G\~64G LPDDR5内存;功耗满足7\~60W,提供算力34 TOPS\~275 TOPS的AI算力;Orin系列是包含7个相同架构的模组其性能是上一代AI推理的8倍并支持高速接口;强大的软件堆栈包含预训练的 AI 模型、参考 AI 工作流和垂直应用框架,可加速生成性 AI 的端到端开发,以及边缘 AI 和机器人应用。 Thor:12\~14核 Arm® Neoverse®-V3AE 64 位 CPU@2.6G+(64\~96)X(1536\~2560)核Blackwell 架构 GPU+128G LPDDR5X内存,提供1200~2070TFLOPS(FP4)算力;功耗在40~75W,与AGX Orin相比,Jetson Thor 系列模组的 AI 计算性能提高至 7.5 倍以上,能效提高至 3.5 倍。应用在人形机器人、空间智能、多传感器处理、生成式AI等多个场景。 软件 NVIDIA Jetson软件是永远边缘构建、部署和扩展人形机器人及生成式AI应用的旗舰平台。它支持全系列Jetson模块,为从原型开发到量产提供统一且可扩展的基础。NVIDIA JetPack SDK赋能实时传感处理、多摄像头追踪,以及如操作和导航等先进机器人功能,集成于强大的AI生态之中。开发者可借助诸如NVIDIA Holoscan(传感器流式处理)和Metropolis VSS(视频分析)等集成框架。通过NVIDIA Isaac机器人工作流程,包括想NVIDIA GROOT N1等基础生成式AI模型,Jetson软件为机器人实现快速、精准、变革性的AI赋能和规模化部署提供支持。 JetPack SDK:是一套完整的软件套件,用于NVIDIA Jetson平台上开发和部署AI驱动的边缘应用。 Holoscan传感器桥接器:将边缘传感器连接到AI工作流,以实现实时、高性能的传感器数据处理。 Jetson AI Lab:由NVIDIA工具和社区项目提供支持,激发机器人和生成式AI领域的创新和动手探索。 NVIDIA Isaac:提供NVIDIA CUDA加速库、框架和AI模型,用一个构建自主机器人,包括ARM、机械臂和人形机器人。 NVIDIA Metropolis:为智慧城市、工业和零售业开发和部署视觉AI应用,并在边缘进行实时视频分析。 JetPack SDK JetPack是NVIDIA Jetson平台官方软件套件,涵盖丰富的工具和库,可用于大招AI赋能边缘应用。目前最新的版本是JetPack7,采用Linux kernel 6.8及ubuntu 24.04 LTS,模块化云原生架构,结合最新的NVIDIA计算堆栈,无缝衔接NVIDIA AI工作流。 JetPack组件由AI计算堆栈、AI框架、Linux组件几个部分组成。 AI计算堆栈:由CUDA、cuDNN、TensorRT组成;用于提供硬件GPU的加速底层接口;CUDA提供NVIDIA GPU 上编写和运行通用计算程序的能力;cuDNN在CUDA之上的深度神经网络算子库,提供高度优化的深度学习核心算子(卷积、池化、激活函数、RNN/LSTM、注意力等)。Pytorch/TensorFlow调用cuDNN中的Conv2d、RNN等。TensorRT推理优化器,只负责推理不负责训练,把训练好的模型转换成高效的 GPU 可执行引擎底层依赖CUDA/cuDNN。与pytorch、TensorFlow不同其即是训练+推理框架。但相对pytorch、TensorFlow的推理,TensorRT性能效率更高。 AI框架:由pytorch、vLLM、SGLang、Triton推理服务器等部分组成。vLLM是便捷、快速的大型语言模型推理与服务库,SGLang 是专为大语言模型及视觉语言模型打造的高效推理框架。 Linux组件:主要是基础系统组件,基于ubuntu系统构建,提供刷机、安全、OTA、图形库(OpenGL、Vulkan、EGL等)、多媒体API、计算机视觉库(OpenCV、VisionWorks)等。 其他组件:Jetson平台服务、云原生设计、Nsight开发工具组成;平台服务提供预构建和可定制的云原生软件服务;云原生设计师提供容器化开发、kubernetes和微服务;Nsight提供强大的分析、调试、性能分析功能,在AI、图形和计算工作负载中优化GPU加速应用。 在JetPack SDK上各种应用SDK,如提供NVIDIA DeepStream SDK、NVIDIA Isaac ROS、NVIDIA Holoscan SDK。 Metropolis VIDIA Metropolis 是一个视觉 AI 应用平台和合作伙伴生态系统,可简化从边缘到云端的视觉 AI 智能体的开发、部署和可扩展性。可以做自动化视觉检查、智能交通系统、工业自动化、智能零售商店等等。 模型:可访问各种先进的AI模型,构建视觉AI应用,支持VLM等;提供TAO工具套件。对模型训练、适应和优化上手简单,不需要专业的AI知识或大型训练数据集,使用自己的数据微调即可完成。 工具:提供AI智能体Blueprints,借助大模型构建智能体,分析、解释和处理大量视频数据,以提供关键见解,帮助各行各业优化流程、提高安全性并降低成本。提供NVIDIA NIM一套易于使用的推理微服务,NIM 支持各种 AI 模型 (包括基础模型、LLM、VLM 等) ,可确保使用行业标准 API 在本地或云端进行无缝、可扩展的 AI 推理。提供DeepStream SDK,是基于 GStreamer 的完整流分析工具包。 数据:Omniverse集成 OpenUSDNVIDIA RTX™ 渲染技术,以及 物理 AI 集成到现有软件工具和仿真工作流中进行开发和测试 。NVIDIA Cosmos™ 是一个先进的生成式AI平台世界基础模型( WFM) 、高级标记器、护栏以及加速数据处理和管护流程,旨在加速物理 AI系统。NVIDIA Isaac SIM开发者在物理精准的虚拟环境中生成合成图像和视频数据,以训练自定义视觉AI模型。 Isaac NVIDIA Isaac AI机器人开发平台有NVIDIA CUDA加速库、应用框架和AI模型组成,可加速自主移动机器人、手臂和操作器以及人形机器人等。 NVIDIA Robotis提供了全栈、加速库和优化的AI模型,能够高效开发、训练、仿真、部署机器人系统。 Isaac ROS:机器人操作系统,是基于开源ROS2构建,包含了NVIDIA CUDA加速计算包的集合,便于简化和加速高级AI机器人应用开发。 Isaac Manipulator:基于Isaac ROS构建,支持开发AI驱动的机械臂,这些机械臂可以无缝感知和理解环境并与环境进行交互。 Isaac Perceptor:基于Isaac ROS构建,支持开发先进的自主移动机器人,能够在仓库货工厂等非结构化环境中进行感知和定位。 Isaac GR00T:用于通用机器人基础模型和数据流水线,以加速人形机器人的开发。 还提供了基于物理的虚拟环境中设计、仿真、测试和训练的框架。NVIDIA Isaac Sim和NVIDIA Isaac Lab。 NVIDIA Isaac Sim:是一款基于 NVIDIA Omniverse 构建的开源参考应用,使开发者能够在基于物理的虚拟环境中模拟和测试 AI 驱动的机器人开发解决方案。 NVIDIA Isaac Lab:Isaac Lab 基于 NVIDIA Isaac Sim™ 开发,使用 NVIDIA®PhysX® 以及基于物理性质的 NVIDIA RTX™ 渲染提供高保真物理仿真。 Holoscan SDK NVIDIA Holoscan 将传感器数据传输到 GPU 进行实时推理,从而加速边缘 AI 开发。 Holoscan 传感器桥接器:可在高吞吐量传感器数据与 GPU 之间提供关键链接,从而无缝集成异构传感器数据。它可标准化并管理从各种传感器接口 (如摄像头输入、超声波或内窥镜视频) 中的数据提取,确保以低延迟、同步和可靠的方式传输数据,从而实现实时 AI 处理。 NVIDIA IGX ORIN:是一个结合了企业级硬件、软件和支持的工业级平台,可在生产就绪型硬件上进行部署。虽然 Holoscan SDK 可在您的目标设备上灵活部署,但 IGX 使公司能够专注于应用开发,并更快地实现 AI 的优势。 Jetson AI Lab Jetson AI Lab 由 NVIDIA 工具和社区项目提供支持,其提供了各种大模型的快速部署示例,如大语言模型LLM/SLM、视觉语言大模型VLM、Web UI等等。 如上图,如果要运行一个模型,就可以通过如上图示例直接获取到运行命令,还可以调整参数。更详细的教程参考:https://www.jetson-ai-lab.com/tutorial-intro.html 参考:https://www.nvidia.cn/autonomous-machines/ -
Jetson nano平台随记
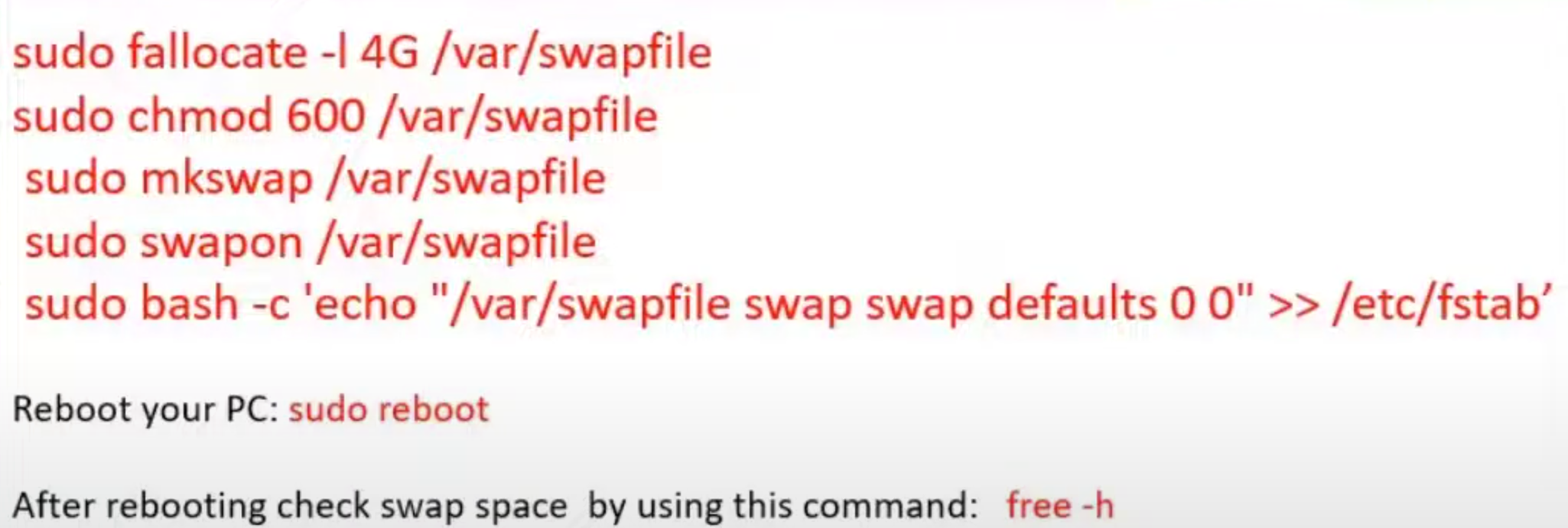
环境准备 烧录镜像 下载NVIDIA jetson nano镜像,其镜像是基于ubuntu18.04修改。使用开源的balenaEtcher烧录器写到SD卡上,然后插卡启动 网络准备 买一个无线网卡然后安装好驱动配置好wifi连接。 远程访问 方法1: 在nano上安装xrdp的方式,window就可以远程桌面访问。 方法2:在nano上安装VNC,远程访问设备需要下载VNC客户端,支持ubuntu系统。 pyhton独立环境 类型conda activate的环境 sudo apt-get install python3-pip pip3 install virturalenv 创建一个环境 python3 -m virtualenv -p python3 env --system-site-packages 激活环境 source env/bin/activate 图像和视频 主要是https://github.com/thehapyone/NanoCamera 安装opencv 创建一个swap空间,否则内存可能不够。 在安装opencv前,还要准备一下环境 使用wget下载opencv的包。 wget -O opencv_contrib.zip https://github.com/openc/opencv_corntrib/archive/4.5.1.1.zip 使用cmake进行编译。 使用jtop可以查看系统统计信息,前提是要按照pip install -U jeston-stats 硬件接上CSI的摄像头,接上之后可以在/dev/videox 看到节点。可以使用下面的命令测试就可以看到图像。 nvgstcaptrue-1.0 --orientation=2 --cap-dev-node=1指定节点如/dev/video1 读取显示 import cv2 img = cv2.imread('/assets/a.jpg') cv2.imshow("Output",img) cv2.waitkey(0) 对于平台CSI摄像头需要import nanocamera import nanocamera as nano camera = nano.Camera(flip=2, width=640,height=480,fps=30) -
SmolVLA 异步推理:远程 Policy Server 与本地 Client 实操
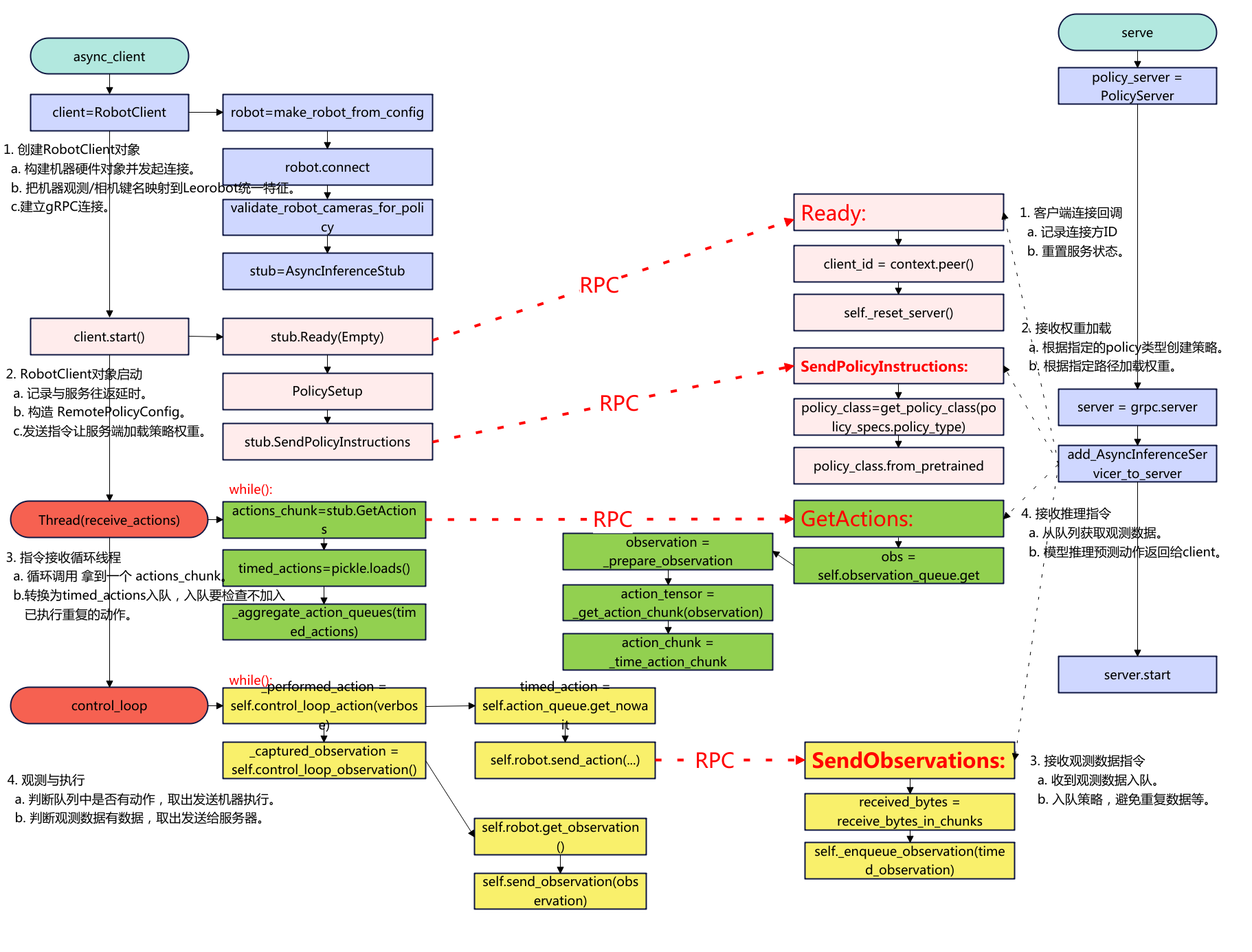
概述 本文记录lerobot smolvla异步推理实践,将SmolVLA的策略server部署到AutoDL上,真机client在本地笔记本上运行。 下面是代码的流程图: 环境准备 先登录AutoDL事先搭建好lerobot的环境,这里就不再重复了,参考往期文章。lerobot环境搭建好后,需要先安装smolvla和gRPC。 # 建议先升级打包工具 python -m pip install -U pip setuptools wheel pip install -e ".[smolvla]" # 安装 gRPC 及相关 python -m pip install grpcio grpcio-tools protobuf 服务器 python src/lerobot/scripts/server/policy_server.py --host=127.0.0.1 --port=8080 --fps=30 --inference_latency=0.033 --obs_queue_timeout=2 启动成功后的日志如下: python src/lerobot/scripts/server/policy_server.py --host=127.0.0.1 --port=8080 --fps=30 --inference_latency=0 --obs_queue_timeout=2 INFO 2025-08-28 10:33:07 y_server.py:384 {'fps': 30, 'host': '127.0.0.1', 'inference_latency': 0.0, 'obs_queue_timeout': 2.0, 'port': 8080} INFO 2025-08-28 10:33:07 y_server.py:394 PolicyServer started on 127.0.0.1:8080 被客户端连接后的日志: INFO 2025-08-28 10:40:42 y_server.py:104 Client ipv4:127.0.0.1:45038 connected and ready INFO 2025-08-28 10:40:42 y_server.py:130 Receiving policy instructions from ipv4:127.0.0.1:45038 | Policy type: smolvla | Pretrained name or path: outputs/smolvla_weigh_08181710/pretrained_model | Actions per chunk: 50 | Device: cuda Loading HuggingFaceTB/SmolVLM2-500M-Video-Instruct weights ... INFO 2025-08-28 10:40:54 odeling.py:1004 We will use 90% of the memory on device 0 for storing the model, and 10% for the buffer to avoid OOM. You can set `max_memory` in to a higher value to use more memory (at your own risk). Reducing the number of VLM layers to 16 ... Loading weights from local directory INFO 2025-08-28 10:41:14 y_server.py:150 Time taken to put policy on cuda: 32.3950 seconds INFO 2025-08-28 10:41:14 ort/utils.py:74 <Logger policy_server (NOTSET)> Starting receiver INFO 2025-08-28 10:41:14 y_server.py:175 Received observation #0 | Avg FPS: 3.45 | Target: 30.00 | One-way latency: -9.22ms INFO 2025-08-28 10:41:14 y_server.py:205 Running inference for observation #0 (must_go: True) INFO 2025-08-28 10:41:15 ort/utils.py:74 <Logger policy_server (NOTSET)> Starting receiver INFO 2025-08-28 10:41:15 y_server.py:175 Received observation #0 | Avg FPS: 3.45 | Target: 30.00 | One-way latency: -9.58ms 服务器仅本地监听(12.0.0.1),这样不暴露公网,客户端通过SSH隧道安全转发。 nohup python src/lerobot/scripts/server/policy_server.py --host=127.0.0.1 --port=8080 --fps=30 --inference_latency=0.033 --obs_queue_timeout=2 >/tmp/policy_server.log 2>&1 & 也可以选择后台运行。 客户端 建立SSH转发 在本地客户端线建立SSH本地端口转发(隧道) ssh -p <服务器ssh的port> -fN -L 8080:127.0.0.1:8080 <用户名@服务器ssh的ip或域名> 如:ssh -p 20567 -fN -L 8080:127.0.0.1:8080 root@connect.xx.xxx.com 如果不想后台运行,运行在前台(Crtl+C结束) ssh -p 20567 -N -L 8080:127.0.0.1:8080 root@connect.xx.xxx.com 本地运行 python src/lerobot/scripts/server/robot_client.py \ --robot.type=so101_follower --robot.port=/dev/ttyACM0 --robot.id=R12252801 \ --robot.cameras="{ handeye: {type: opencv, index_or_path: 6, width: 640, height: 480, fps: 30}, fixed: {type: opencv, index_or_path: 0, width: 640, height: 480, fps: 30}}" \ --policy_type=smolvla \ --pretrained_name_or_path=outputs/smolvla_weigh_08181710/pretrained_model \ --policy_device=cuda \ --actions_per_chunk=50 \ --fps=30 \ --server_address=localhost:8080 \ --chunk_size_threshold=0.8 \ --debug_visualize_queue_size=True 其他参数 --debug_visualize_queue_size=True: 执行结束后可视化队列情况。 需要安装 pip install matplotlib。 --aggregate_fn_name=conservative:当新动作到达时,如果队列中已经存在相同时间步的动作,系统会使用聚合函数来合并它们。如果为latest_only(默认),只用最新动作,这样可能会抖动剧烈。 --pretrained_name_or_path 会在“服务器上”加载。需要确保服务器上outputs/smolvla_weigh_08181710路径有权重文件。 连接执行的日志如下: python src/lerobot/scripts/server/robot_client.py --robot.type=so101_follower --robot.port=/dev/ttyACM0 --robot.id=R12252801 --robot.cameras="{ handeye: {type: opencv, index_or_path: 6, width: 320, height: 240, fps: 25}, fixed: {type: opencv, index_or_path: 0, width: 320, height: 240, fps: 25}}" --policy_type=smolvla --pretrained_name_or_path=outputs/smolvla_weigh_08181710/pretrained_model --policy_device=cuda --actions_per_chunk=50 --chunk_size_threshold=0.8 --fps=30 --server_address=localhost:8080 --aggregate_fn_name=average INFO 2025-08-28 10:40:38 t_client.py:478 {'actions_per_chunk': 50, 'aggregate_fn_name': 'average', 'chunk_size_threshold': 0.8, 'debug_visualize_queue_size': False, 'fps': 30, 'policy_device': 'cuda', 'policy_type': 'smolvla', 'pretrained_name_or_path': 'outputs/smolvla_weigh_08181710/pretrained_model', 'robot': {'calibration_dir': None, 'cameras': {'fixed': {'color_mode': <ColorMode.RGB: 'rgb'>, 'fps': 25, 'height': 240, 'index_or_path': 0, 'rotation': <Cv2Rotation.NO_ROTATION: 0>, 'warmup_s': 1, 'width': 320}, 'handeye': {'color_mode': <ColorMode.RGB: 'rgb'>, 'fps': 25, 'height': 240, 'index_or_path': 6, 'rotation': <Cv2Rotation.NO_ROTATION: 0>, 'warmup_s': 1, 'width': 320}}, 'disable_torque_on_disconnect': True, 'id': 'R12252801', 'max_relative_target': None, 'port': '/dev/ttyACM0', 'use_degrees': False}, 'server_address': 'localhost:8080', 'task': '', 'verify_robot_cameras': True} INFO 2025-08-28 10:40:40 a_opencv.py:179 OpenCVCamera(6) connected. INFO 2025-08-28 10:40:41 a_opencv.py:179 OpenCVCamera(0) connected. INFO 2025-08-28 10:40:41 follower.py:104 R12252801 SO101Follower connected. WARNING 2025-08-28 10:40:42 ils/utils.py:54 No accelerated backend detected. Using default cpu, this will be slow. WARNING 2025-08-28 10:40:42 /policies.py:80 Device 'cuda' is not available. Switching to 'cpu'. WARNING 2025-08-28 10:40:42 ils/utils.py:54 No accelerated backend detected. Using default cpu, this will be slow. WARNING 2025-08-28 10:40:42 /policies.py:80 Device 'cuda' is not available. Switching to 'cpu'. INFO 2025-08-28 10:40:42 t_client.py:121 Initializing client to connect to server at localhost:8080 INFO 2025-08-28 10:40:42 t_client.py:140 Robot connected and ready INFO 2025-08-28 10:40:42 t_client.py:163 Sending policy instructions to policy server INFO 2025-08-28 10:41:14 t_client.py:486 Starting action receiver thread... INFO 2025-08-28 10:41:14 t_client.py:454 Control loop thread starting INFO 2025-08-28 10:41:14 t_client.py:280 Action receiving thread starting INFO 2025-08-28 10:41:15 t_client.py:216 Sent observation #0 | INFO 2025-08-28 10:41:15 t_client.py:469 Control loop (ms): 288.72 INFO 2025-08-28 10:41:15 t_client.py:216 Sent observation #0 | INFO 2025-08-28 10:41:15 t_client.py:469 Control loop (ms): 132.22 INFO 2025-08-28 10:41:15 t_client.py:216 Sent observation #0 | INFO 2025-08-28 10:41:15 t_client.py:469 Control loop (ms): 127.84 INFO 2025-08-28 10:41:15 t_client.py:216 Sent observation #0 | INFO 2025-08-28 10:41:15 t_client.py:469 Control loop (ms): 123.95 INFO 2025-08-28 10:41:15 t_client.py:216 Sent observation #0 | INFO 2025-08-28 10:41:15 t_client.py:469 Control loop (ms): 140.21 INFO 2025-08-28 10:41:15 t_client.py:469 Control loop (ms): 0.54 INFO 2025-08-28 10:41:15 t_client.py:469 Control loop (ms): 0.42 如果使用ACT策略,对于ACT来说chunk_size_threshold不要设置太大,实测发现不然一个chunk到下一个chunk抖动比较严重 python src/lerobot/scripts/server/robot_client.py \ --robot.type=so101_follower \ --robot.port=/dev/ttyACM0 \ --robot.id=R12252801 \ --robot.cameras="{ handeye: {type: opencv, index_or_path: 6, width: 640, height: 480, fps: 30}, fixed: {type: opencv, index_or_path: 0, width: 640, height: 480, fps: 30}}" \ --policy_type=act \ --pretrained_name_or_path=outputs/act_weigh_07271539/pretrained_model \ --policy_device=cuda \ --actions_per_chunk=100 \ --fps=30 \ --server_address=localhost:8080 \ --chunk_size_threshold=0.1 以上就是用SSH隧道的方式实现异步推理的过程。 参考:https://hugging-face.cn/docs/lerobot/async 常见问题 (0)服务器监控日志分析 Received observation #136:服务器接收到第136个观察数据 Avg FPS: 11.52:实际观测数据帧率,根据客户端每秒采样时间计算,跟服务端没有关系。 Target:目标设置的观测数据帧率,如15帧/s。 One-way latency: 客户端到服务器的单向网络延迟为1.71ms。 inference time: 模型推理耗时时长为1667ms。 action chunk #136:生成了第136个动作块。 Total time: 推理+序列化总处理时长。 (1)服务端实际的观测帧率低 INFO 2025-08-29 09:47:05 y_server.py:175 Received observation #573 | Avg FPS: 1.20 | Target: 30.00 | One-way latency: 35.78ms 可以看到上面的收到的观测帧率平均只有1.2,看看服务端计算FPS的逻辑。 # 每次接收观测时调用 self.total_obs_count += 1 # 包括所有接收的观测(包括被过滤的) total_duration = current_timestamp - self.first_timestamp avg_fps = (self.total_obs_count - 1) / total_duration 影响服务端的接受观测帧帧率的有客户端观测发送频率低,服务端观测被过滤,推理时间长间接影响 关于客户端观测数据的发送限制如下: # 只有当队列大小/动作块大小 <= 阈值时才发送观测 if queue_size / action_chunk_size <= chunk_size_threshold: send_observation() 可以看到只有满足上面的小于动作阈值才会发送,所以要加大发送的帧率需要改大阈值chunk_size_threshold,减少actions_per_chunk,减少queue_size。 对于ACT策略的FPS 低可能不是问题,这是观察发送频率,不是控制频率,因为ACT 策略就是低频观察,高频执行,主要看机器是不是以30FPS动作执行就好。smolvla也是同样的。因此有时候不要过于误解这个观测帧率,太高的观测帧率也不一定是好事。 (2)观测数据被过滤 y_server.py:191 Observation #510 has been filtered out 服务端会根据这次和上次的关节角度计算欧拉来判断相似性,默认的阈值参数是1,可以改小一点,对相似性的判断严苛一下。 def observations_similar( obs1: TimedObservation, obs2: TimedObservation, lerobot_features: dict[str, dict], atol: float = 1 ) -> bool: ...... return bool(torch.linalg.norm(obs1_state - obs2_state) < atol) 如上修改atol的值,可以改小为如0.5。 总结一下: 对于分布式推理不要过于去纠结实际的观测帧率,而是应该看控制的实际帧率,只要控制动作的帧率(如下的延时,大概就是30fps)是满足的就是可以的,也就是说动作队列中动作不要去获取的时候是空。 对于参数优化重点看服务端的推理延时和客户端的队列管理。 服务端是可以设置推理延时的 # 推理延迟控制 --inference_latency=0.033 # 模型推理延迟(秒) # 观察队列管理 --obs_queue_timeout=2 # 获取观测队列超时时间(秒) 客户端动作管理 --actions_per_chunk=100 # 一个动作块的序列大小,越大推理负载就重 --chunk_size_threshold=0.5 # 队列阈值,越大缓存的动作序列越多,越小实时性越好。 --fps=30 # 控制频率 如果要低延时那么就需要把fps提高,也就是服务端的推理时间设置小,客户端的chunk、threshold要小,fps要高。 -

网站github page同步
准备 下载同步的仓库 mkdir blog git clone git@github.com:laumy0929/wordpress-export-to-markdown.git git clone git@github.com:laumy0929/notes.git git clone git@github.com:laumy0929/note_page.git wordpress-export-to-markdown: 为wordpress转换为markdown工具。 notes:生成github page的工具。 note_page:实际的github io page网站。 导出转换 在wordpress后台导出文档,得到一个备份文件laumy.WordPress.2025-10-26.xml。 cd wordpress-export-to-markdown/ ./auto.sh ../laumy.WordPress.2025-08-15.xml ../output 这样就将wordpress转换为markdown文件了,转换完成之后将源文件拷贝到notes/doc目录下。 wordpress-export-to-markdown需要安装node.js,如果没有安装按照下面方法安装。 curl -fsSL https://deb.nodesource.com/setup_21.x | sudo -E bash - sudo apt-get install -y nodejs npm install chalk npm install markdown转换网站 先创建环境 cd notes/ python3 -m venv .venv && source .venv/bin/activate pip install -r requirements.txt 接着执行命令将会自动上传 ./deploy.sh --deploy 网站地址:https://laumy0929.github.io/note_page/ -
LeRobot SmolVLA:从训练到推理链路剖析
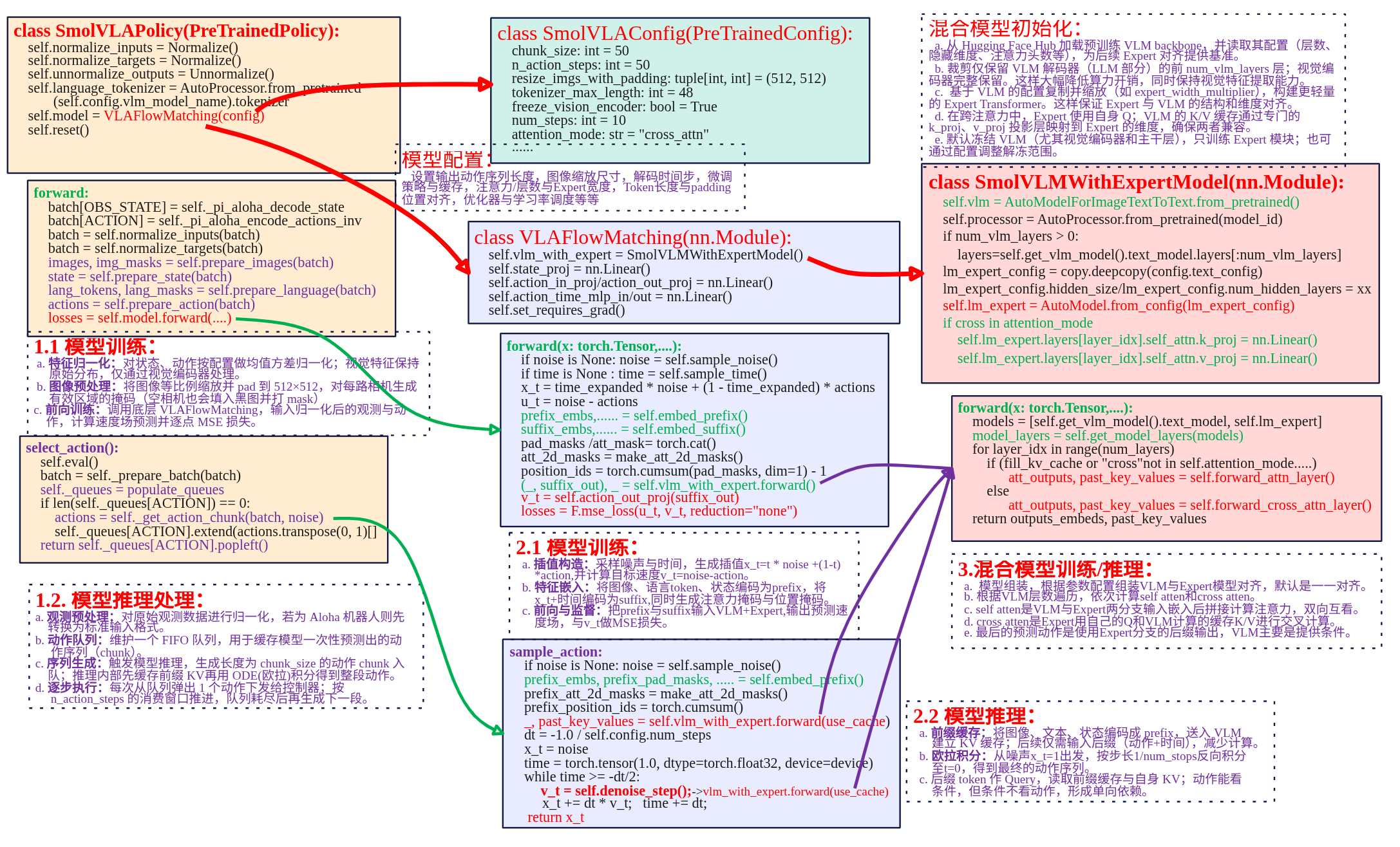
框架 本文主要对lerobot SmolVLA策略代码进行分析,下面是策略实现关键部分框图。 SmolVLAPolicay类封装向上提供策略的调用。SmolVLAConfig是对SmolVLA策略的配置,用于配置输出动作序列长度、观测图像输入后到模型的缩放尺寸以及微调策略等等。SmolVLAPolicay类中关键的成员是VLAFlowMatching类,是实现SmolVLA模型flow matching机制训练、推理的核心。在VLAFlowMatching类中关系成员是SmolVLMWithExpertModel类,其定义了VLM+Expert模型具体实现。 SmolVLA策略实现主要涉及SmolVLAPolicy、VLAFlowMatching 、SmolVLMWithExperModel三个类来实现。就以模型训练、模型推理两条主线来进行总结。 训练 训练过程可以分为一下几个核心部分: 数据输入处理:图像、文本和状态通过各自处理方法嵌入并标准化,合并成统一的输入,供后续层次处理。 VLM与专家模型交互前向传播:图像、文本和状态数据通过VLM和专家模型进行多层次的自注意力和交叉注意力计算,得到联合特征表示。 损失计算与优化:通过计算预测动作和目标动作之间的损失,具体是速度场的损失,使用反向传播更新参数。 模型参数冻结与训练策略:通过冻结不必要的模型部分(VLM),专注优化重要部分,减少计算的开销。 输入处理 SmolVLA模型分为前缀prefix、后缀suffix输入。前缀主要是观测端数据由图像、文本和机器的状态嵌入构成,提供给VLM处理,目的是为模型提供上下文信息,理解任务的背景。后缀是用于生成过程中,输入的是噪声动作+时间步,经过Expert模型处理输出具体的预测动作。 (1)前缀prefix嵌入 def embed_prefix(self, images, img_masks, lang_tokens, lang_masks, state: torch.Tensor = None): embs = [] pad_masks = [] att_masks = [] # 处理图像 for _img_idx, (img, img_mask) in enumerate(zip(images, img_masks)): img_emb = self.vlm_with_expert.embed_image(img) embs.append(img_emb) pad_masks.append(img_mask) # 处理语言 lang_emb = self.vlm_with_expert.embed_language_tokens(lang_tokens) embs.append(lang_emb) pad_masks.append(lang_masks) # 处理状态 state_emb = self.state_proj(state) embs.append(state_emb) state_mask = torch.ones_like(state_emb) pad_masks.append(state_mask) # 合并所有嵌入 embs = torch.cat(embs, dim=1) pad_masks = torch.cat(pad_masks, dim=1) att_masks = torch.cat(att_masks, dim=1) return embs, pad_masks, att_masks 代码的流程是依次对输入图像、语言、机器状态进行分别做embedding,然后进行按列合并为一个前缀输入。 图像嵌入:通过embed_image方法转换为嵌入表示,每个图像的嵌入被添加到embs列表中,img_mask则记录图像的有效区域。 文本嵌入:通过embed_language_tokens() 被转换为嵌入表示,lang_emb 是语言的嵌入,包含了语言的语法和语义信息。 状态嵌入:状态信息通过 state_proj() 映射到与图像和文本相同维度的空间,得到 state_emb。 最终图像嵌入、文本嵌入和状态嵌入通过 torch.cat() 方法按列合并成一个大的 前缀输入(Prefix)。pad_masks 和 att_masks 也被合并成一个统一的输入,确保每个模态的信息能够与其他模态的输入一起传递。 图像和文本嵌入调用已经隐式包含了位置编码,状态信息state_proj 转换为嵌入,尽管没有显式的位置信息,但会在模型中通过与其他模态嵌入的融合获取上下文信息。 (2)后缀Suffix嵌入 def embed_suffix(self, noisy_actions, timestep): embs = [] pad_masks = [] att_masks = [] # 使用 MLP 融合时间步长和动作信息 action_emb = self.action_in_proj(noisy_actions) device = action_emb.device bsize = action_emb.shape[0] dtype = action_emb.dtype # 使用正弦-余弦位置编码生成时间嵌入 time_emb = create_sinusoidal_pos_embedding( timestep, self.vlm_with_expert.expert_hidden_size, self.config.min_period, self.config.max_period, device=device, ) time_emb = time_emb.type(dtype=dtype) # 将时间嵌入和动作嵌入结合 time_emb = time_emb[:, None, :].expand_as(action_emb) action_time_emb = torch.cat([action_emb, time_emb], dim=2) action_time_emb = self.action_time_mlp_in(action_time_emb) action_time_emb = F.silu(action_time_emb) # swish == silu action_time_emb = self.action_time_mlp_out(action_time_emb) # 将生成的动作嵌入加入到输入中 embs.append(action_time_emb) bsize, action_time_dim = action_time_emb.shape[:2] action_time_mask = torch.ones(bsize, action_time_dim, dtype=torch.bool, device=device) pad_masks.append(action_time_mask) # 设置注意力掩码,防止图像、语言和状态的输入与动作输入相互影响 att_masks += [1] * self.config.chunk_size embs = torch.cat(embs, dim=1) pad_masks = torch.cat(pad_masks, dim=1) att_masks = torch.tensor(att_masks, dtype=embs.dtype, device=embs.device) att_masks = att_masks[None, :].expand(bsize, len(att_masks)) return embs, pad_masks, att_masks 后缀的输入主要是提供给Expert专家模型用于flow matching预测出输出,输入是噪声动作(noisy actions)+时间步长(timestep)。上述代码可以分为以下几个部分: 时间步长嵌入:时间步长(timestep)用于表示当前的生成步骤,生成一个正弦-余弦位置编码(Sine-Cosine Positional Embedding)。create_sinusoidal_pos_embedding() 使用正弦和余弦函数生成时间嵌入,增强模型对时序的理解。 动作嵌入:动作通过 action_in_proj 进行嵌入,得到 action_emb。这一步是将生成的动作(采样的噪声动作)转化为嵌入表示。 融合时间和动作:动作嵌入与时间嵌入(time_emb)通过 torch.cat() 进行拼接,形成一个新的包含时间信息的动作嵌入。这样,生成的动作不仅包含来自环境的信息,还加入了时间步长的变化。 MLP处理:合并后的动作嵌入通过 action_time_mlp_in 和 action_time_mlp_out 层进行处理。这个过程是对动作嵌入进行进一步的处理,确保其能够适应后续的生成任务。 最终,生成的动作嵌入被加入到 embs 列表中,并通过 torch.cat() 合并为一个统一的后缀输入。这个后缀输入将与前缀输入一起通过 Transformer 层进行处理。 前向传播 forward是整个前向传播的核心,将将输入组合后通过模型计算输出。 def forward( self, images, img_masks, lang_tokens, lang_masks, state, actions, noise=None, time=None ): # 1. 前缀输入的生成 prefix_embs, prefix_pad_masks, prefix_att_masks = self.embed_prefix( images, img_masks, lang_tokens, lang_masks, state ) # 2. 后缀输入的生成 suffix_embs, suffix_pad_masks, suffix_att_masks = self.embed_suffix(actions, time) # 3. 拼接前缀和后缀的嵌入 pad_masks = torch.cat([prefix_pad_masks, suffix_pad_masks], dim=1) att_masks = torch.cat([prefix_att_masks, suffix_att_masks], dim=1) # 4. 计算注意力掩码 att_2d_masks = make_att_2d_masks(pad_masks, att_masks) position_ids = torch.cumsum(pad_masks, dim=1) - 1 # 5. 前向计算 (_, suffix_out), _ = self.vlm_with_expert.forward( attention_mask=att_2d_masks, position_ids=position_ids, past_key_values=None, inputs_embeds=[prefix_embs, suffix_embs], use_cache=False, fill_kv_cache=False, ) # 6. 速度场预测计算损失 suffix_out = suffix_out[:, -self.config.chunk_size :] suffix_out = suffix_out.to(dtype=torch.float32) v_t = self.action_out_proj(suffix_out) losses = F.mse_loss(v_t, actions, reduction="none") return losses 代码调用前缀、后缀输入然后进行拼接得到inputs_embeds,然后再计算注意力的掩码就可以调用VLM+Expert模型进行前向计算。在前向计算中有两个参数use_cache 和 fill_kv_cache 参数,这两个参数的设置控制 key-value 缓存 的使用。 (1)模型组合 models = [self.get_vlm_model().text_model, self.lm_expert] model_layers = self.get_model_layers(models) def get_model_layers(self, models: list) -> list: vlm_layers = [] expert_layers = [] multiple_of = self.num_vlm_layers // self.num_expert_layers for i in range(self.num_vlm_layers): if multiple_of > 0 and i > 0 and i % multiple_of != 0: expert_layer = None else: expert_layer_index = i // multiple_of if multiple_of > 0 else i expert_layer = models[1].layers[expert_layer_index] vlm_layers.append(models[0].layers[i]) expert_layers.append(expert_layer) return [vlm_layers, expert_layers] 模型混合主要是生成一个混合的模型层列表,通过get_model_layers函数计算并返回 VLM 层和 Expert 层的对齐关系,VLM层和Expert层对齐是基于multiple_of来进行层级分配的。如果某些 VLM 层 没有对应的 Expert 层,则设置为 None,仅由 VLM 层处理。默认情况下VLM和Expert的层数一样都为16,下图看看VLM=8,Expert=4的示例。 因此最终对于SmolVLA来说,模型是一个混合的模型层列表model_layers。可以通过model_layers[i][layer_idx]来访问具体的模型,model_layers[0][x]为VLM模型,model_layers[1][x]为Expert模型。如model_layers[0][2]为第二层的VLM,model_layers[1][2]为第二层的Expert,model_layers[1][1]为None。 (2)处理输入嵌入 for hidden_states in inputs_embeds: if hidden_states is None: continue batch_size = hidden_states.shape[0] 遍历输入嵌入(inputs_embeds),检查是否有无效的输入(即 None),并获取当前批次的大小batch_size。 inputs_embeds:模型的输入嵌入数据,可能包含多种模态的输入(例如,图像嵌入、文本嵌入等)。 hidden_states.shape[0]:获取当前输入数据的批次大小。 (3)自注意力与交叉注意力 num_layers = self.num_vlm_layers head_dim = self.vlm.config.text_config.head_dim for layer_idx in range(num_layers): if ( fill_kv_cache or "cross" not in self.attention_mode or (self.self_attn_every_n_layers > 0 and layer_idx % self.self_attn_every_n_layers == 0) ): att_outputs, past_key_values = self.forward_attn_layer() else: att_outputs, past_key_values = self.forward_cross_attn_layer() 使用VLM层数来进行遍历,因为VLM侧的层数是Expert的一倍。进行如循环根据条件来判断是进行自注意力计算还是交叉注意力计算。 判断使用自注意力的条件是有3种情况(其中一种满足即可): fill_kv_cache:如果需要填充 键值缓存(key-value cache),则使用自注意力计算。 "cross" not in self.attention_mode:如果当前没有启用交叉注意力模式,则使用自注意力。 self_attn_every_n_layers:在每隔 n 层计算自注意力时,执行该条件。通常用于启用跨层的自注意力机制。 具体关于自注意力与交叉注意力计算的细节见后续章节。 (4)残差连接与前馈网络 out_emb += hidden_states after_first_residual = out_emb.clone() out_emb = layer.post_attention_layernorm(out_emb) out_emb = layer.mlp(out_emb) out_emb += after_first_residual 残差连接:每一层都使用残差连接,将当前层的输出与原始输入相加,防止深层网络的梯度消失问题。 前馈网络(MLP):通过前馈神经网络(通常包括一个隐藏层和激活函数)进行处理,进一步捕捉输入的非线性关系。 (5)输出处理 outputs_embeds = [] for i, hidden_states in enumerate(inputs_embeds): if hidden_states is not None: out_emb = models[i].norm(hidden_states) outputs_embeds.append(out_emb) else: outputs_embeds.append(None) return outputs_embeds, past_key_values 遍历输入嵌入(inputs_embeds),对每个有效的 hidden_states 进行 归一化处理(models[i].norm())。如果嵌入无效(即 None),则直接将 None 放入输出列表中,以保持输入结构的对齐。最终返回 处理后的嵌入 和 past_key_values(如果有的话)。 归一化(通常是层归一化)确保嵌入在后续计算中具有更好的数值稳定性,帮助模型学习。对缺失的嵌入(None)进行特殊处理,主要是VLM+Expert对齐时,Expert通常为VLM的一半,而模型遍历是时按照VLM层次来遍历的,所以有一半的Expert是None,但是这部的None不能在处理VLM层的时候断掉Expert的输入,否则Expert模型梯度链就断了。 损失计算 SmolVLAPolicy.forward(...) ...... 调 VLAFlowMatching 计算逐样本/逐步/逐维损失(不聚合) losses = self.model.forward(images, img_masks, lang_tokens, lang_masks, state, actions, noise, time) if actions_is_pad is not None: in_episode_bound = ~actions_is_pad losses = losses * in_episode_bound.unsqueeze(-1) # 去掉为对齐而pad出的 action 维度 losses = losses[:, :, : self.config.max_action_dim] # 聚合为标量 loss(反向传播用) loss = losses.mean() return loss, {"loss": loss.item()} 在SmolVLAPolicy.forward(...)调用VLAFlowMatching.forward计算返回损失,下面直接来看VLAFlowMatching.forward。 def forward(self, images, img_masks, lang_tokens, lang_masks, state, actions, noise=None, time=None) -> Tensor: # ① 采样噪声与时间 if noise is None: noise = self.sample_noise(actions.shape, actions.device) # ~N(0,1) if time is None: time = self.sample_time(actions.shape[0], actions.device) # Beta(1.5,1.0)→偏向 t≈1 # ② 合成中间点 x_t 与“真向量场” u_t time_expanded = time[:, None, None] # [B,1,1] x_t = time_expanded * noise + (1 - time_expanded) * actions # convex组合 u_t = noise - actions # ③ 前缀/后缀嵌入(图像+文本+状态 | 动作+时间),拼注意力mask/位置id prefix_embs, prefix_pad_masks, prefix_att_masks = self.embed_prefix(images, img_masks, lang_tokens, lang_masks, state) suffix_embs, suffix_pad_masks, suffix_att_masks = self.embed_suffix(x_t, time) pad_masks = torch.cat([prefix_pad_masks, suffix_pad_masks], dim=1) att_masks = torch.cat([prefix_att_masks, suffix_att_masks], dim=1) att_2d_masks = make_att_2d_masks(pad_masks, att_masks) position_ids = torch.cumsum(pad_masks, dim=1) - 1 # ④ 走双塔文本Transformer:prefix + suffix(训练时不建缓存) (_, suffix_out), _ = self.vlm_with_expert.forward( attention_mask=att_2d_masks, position_ids=position_ids, past_key_values=None, inputs_embeds=[prefix_embs, suffix_embs], use_cache=False, fill_kv_cache=False, ) suffix_out = suffix_out[:, -self.config.chunk_size :] # 取后缀对应的输出token # ⑤ Expert头→动作向量场 v_t,并与 u_t 做逐元素 MSE suffix_out = suffix_out.to(dtype=torch.float32) # 数值稳定 v_t = self.action_out_proj(suffix_out) losses = F.mse_loss(u_t, v_t, reduction="none") # [B, T, A] 不聚合 return losses 核心思想还是学习一个向量场 $v_{\theta}(x_t,t)$ 去逼近真实向量场 $u_t = \epsilon - a$,其中 $$ x_t = t \cdot \epsilon + (1 - t) \cdot a, \quad \epsilon \sim \mathcal{N}(0,I) $$ $a$ 是机器真实的动作如舵机的角度,对应上述代码的action;$\epsilon$是noisy action,最开始随机生成采样而来,对应上述的noise。 模型参数 模型参数冻结主要是以下两个方法决定 SmolVLMWithExpertModel.set_requires_grad(管 VLM/Expert的大部分参数); VLAFlowMatching.set_requires_grad(只管 state 的投影头)。 (1)VLM/Expert大部分参数 def set_requires_grad(self): # 1) 冻结视觉编码器(可选) if self.freeze_vision_encoder: self.get_vlm_model().vision_model.eval() for p in self.get_vlm_model().vision_model.parameters(): p.requires_grad = False # 2) 只训练 Expert(常见默认) if self.train_expert_only: self.vlm.eval() for p in self.vlm.parameters(): p.requires_grad = False else: # 3) 非“只训 Expert”时,VLM 只冻结一小部分层,避免 DDP unused params last_layers = [self.num_vlm_layers - 1] if (self.num_vlm_layers != self.num_expert_layers and self.num_vlm_layers % self.num_expert_layers == 0): last_layers.append(self.num_vlm_layers - 2) frozen = ["lm_head", "text_model.model.norm.weight"] for L in last_layers: frozen.append(f"text_model.model.layers.{L}.") for name, p in self.vlm.named_parameters(): if any(k in name for k in frozen): p.requires_grad = False # 4) Expert 侧不训练 lm_head(没用到 LM 头) for name, p in self.lm_expert.named_parameters(): if "lm_head" in name: p.requires_grad = False 冻结视觉编码器:把 VLM 的 vision encoder 切到 eval(),并把其所有参数 requires_grad=False。对于VLM视觉部分已经比较稳定了,若下游数据量不大,继续训练易带来不稳定与显存开销;冻结能省资源并保持视觉表征稳定。 只训练 Expert:把VLM的(视觉编码+LLM)都起到eval且全部冻结。这是一种轻量微调策略——只训练 Expert+ 动作/时间/状态投影头,能在小数据上快速稳定收敛,避免对大模型语义分布造成破坏。 非“只训 Expert”时,VLM 只冻结一小部分层:永远冻结 VLM 的 lm_head(语言模型头,动作任务用不到),冻结text_model.model.norm.weight,降低训练不稳定,冻结最后 1 层; 总结一下: 目标 典型设置 实际可训练部分 轻量微调(默认/推荐起步) freeze_vision_encoder=True + train_expert_only=True Expert 全部层(除 lm_head) + 动作/时间/状态头(VLAFlowMatching 里的 action_in/out_proj、action_time_mlp_、state_proj) 加强表达(部分放开 VLM) freeze_vision_encoder=True/False + train_expert_only=False Expert 全部层 + 大多数 VLM 文本层(但冻结 lm_head、末尾 norm、最后 1–2 层) + 动作/时间/状态头 除了上面的参数之外在 SmolVLMWithExpertModel.train 中又做了一层保险: def train(self, mode=True): super().train(mode) if self.freeze_vision_encoder: self.get_vlm_model().vision_model.eval() if self.train_expert_only: self.vlm.eval() 即使外部调用了 model.train(),被冻的模块仍保持 eval(),避免 Dropout/BN 等训练态行为干扰。是否参与反向仍由 requires_grad 决定;两者配合保证“真冻结”。 (2)state 的投影头 class VLAFlowMatching(nn.Module): def __init__(self, config): super().__init__() self.config = config self.vlm_with_expert = SmolVLMWithExpertModel( ... ) # —— 与动作/状态/时间相关的投影头 —— self.state_proj = nn.Linear( self.config.max_state_dim, self.vlm_with_expert.config.text_config.hidden_size ) self.action_in_proj = nn.Linear(self.config.max_action_dim, self.vlm_with_expert.expert_hidden_size) self.action_out_proj = nn.Linear(self.vlm_with_expert.expert_hidden_size, self.config.max_action_dim) self.action_time_mlp_in = nn.Linear(self.vlm_with_expert.expert_hidden_size * 2, self.vlm_with_expert.expert_hidden_size) self.action_time_mlp_out = nn.Linear(self.vlm_with_expert.expert_hidden_size, self.vlm_with_expert.expert_hidden_size) self.set_requires_grad() # ← 这里调用 ... def set_requires_grad(self): for params in self.state_proj.parameters(): params.requires_grad = self.config.train_state_proj 根据 config.train_state_proj(布尔值)开/关状态投影层 state_proj 的可训练性。这里只对state_proj做控制,这个是把机器人状态(关节角、抓取开合等)映射到 VLM 文本编码器的隐藏维度。不同机器人/任务,状态分布差异很大(量纲、范围、相关性);是否需要学习这个映射,取决于你的数据规模与分布,所以可以根据train_state_proj=True/False来决定是否要训练或冻结。其它头(action_in/out_proj、action_time_mlp_*)对动作/时间更直接,通常都需要学习,因此默认不在这里冻结。 推理 推理的入口函数入口:SmolVLAPolicy.predict_action_chunk ->select_action-> VLAFlowMatching.sample_actions(...),推理跟训练流程大致相同,这里只简单总结一下不同点。 前缀缓存 prefix_embs, prefix_pad_masks, prefix_att_masks = self.embed_prefix(...) prefix_att_2d_masks = make_att_2d_masks(prefix_pad_masks, prefix_att_masks) prefix_position_ids = torch.cumsum(prefix_pad_masks, dim=1) - 1 # 只喂前缀,构建 KV cache _, past_key_values = self.vlm_with_expert.forward( attention_mask=prefix_att_2d_masks, position_ids=prefix_position_ids, past_key_values=None, inputs_embeds=[prefix_embs, None], # ★ 只有前缀 use_cache=self.config.use_cache, # 通常 True fill_kv_cache=True, # ★ 建缓存 ) 与训练的差别是训练不建缓存,推理先把 VLM 的 Q/K/V(更准确:K/V)算出来并存起来(past_key_values),这步只走 self-attn 分支(因为 fill_kv_cache=True),Expert 不参与。另外需要注意的时传递的输入只有prefix_embs而训练是inputs_embeds=[prefix_embs, suffix_embs]既要传递prefix_embs也有传递suffix_embs,这里的后缀编码为插值点的嵌入,即x_t = time_expanded * noise + (1 - time_expanded) * actions。因为没有Expert的输入,所以自注意力算的也只有VLM的输入。 后缀循环 dt = -1.0 / self.config.num_steps x_t = noise # 初始噪声 time = torch.tensor(1.0, ...) while time >= -dt/2: v_t = self.denoise_step(prefix_pad_masks, past_key_values, x_t, time) x_t += dt * v_t # Euler 更新 time += dt return x_t # 作为动作 做 ODE 去噪循环(Euler),每一步只算后缀。与训练的差别是“采一个随机 t 直接监督向量场”,推理是“从 t=1 积分到 t=0”(ODE 解)。这里的 num_steps 控制积分步数(精度/速度权衡)。 denoise_step(...)----> suffix_embs, suffix_pad_masks, suffix_att_masks = self.embed_suffix(x_t, timestep) # 组装 prefix/suffix 的联合注意力掩码(prefix 只提供 pad_2d 以允许被看) full_att_2d_masks = torch.cat([prefix_pad_2d_masks, suffix_att_2d_masks], dim=2) position_ids = prefix_offsets + torch.cumsum(suffix_pad_masks, dim=1) - 1 outputs_embeds, _ = self.vlm_with_expert.forward( attention_mask=full_att_2d_masks, position_ids=position_ids, past_key_values=past_key_values, # ★ 复用 prefix KV inputs_embeds=[None, suffix_embs],# ★ 只有后缀 use_cache=self.config.use_cache, # True fill_kv_cache=False, # ★ 不再建缓存 ) suffix_out = outputs_embeds[1][:, -chunk_size:] v_t = self.action_out_proj(suffix_out) denoise_step(...)拿缓存 + 只喂后缀(前缀为None),分层走 cross/self。VLM 不再重算 Q/K/V,层内 cross-attn 时,Expert 的 Query 去看 prefix 的 K/V 缓存;若该层被 self_attn_every_n_layers 强制 self,则只做 Expert 自注意(VLM 旁路,因为没有输入前缀)。与训练的差别是训练时两侧一起算(inputs_embeds=[prefix, suffix]),且无缓存。 训练 vs 推理 维度 训练(VLAFlowMatching.forward) 推理(sample_actions + denoise_step) 是否用真动作 用,参与构造 x_t,t 与 u_t=noise-actions,形成监督 不用(没有 label),从噪声解 ODE 得动作 时间使用 随机采样 t~Beta(1.5,1.0),单步监督 从 t=1 到 t=0 迭代(步长 dt=-1/num_steps) 是否建 KV Cache 否(use_cache=False, fill_kv_cache=False) 是:先prefix-only 建缓存;循环中 suffix-only 复用缓存 两塔前向喂法 一次性 inputs_embeds=[prefix, suffix] 两段:① [prefix, None](建缓存);② [None, suffix](复用缓存) 层内注意力路由 由 attention_mode / self_attn_every_n_layers 决定,但无缓存上下文 相同路由;cross 时 Expert-Q × cached VLM-KV;self 时只 Expert 自注意 位置编码(RoPE) 每层对参与计算的 Q/K 应用 同上;prefix 的位置在建缓存时用过;suffix 在每步都重算 损失/梯度 MSE(u_t, v_t) → 反向 无损失、无反向 输出后处理 返回标量 loss(policy 中聚合/掩码后) x_t 作为动作 → unnormalize →(可选)Aloha 映射;支持 n-step 队列 注意力 注意力的计算是模型训练和推理的核心,主要涉及自注意力和交叉注意力,这里单独总结一章节进行梳理分析。 自注意力 自注意力的代码注意在forward_attn_layer函数中,接下来根据代码来进行分析。 (1)自注意力QKV计算 query_states = [] key_states = [] value_states = [] 首先定义了Self-Attention 中的 Query、Key 和 Value。这些将用于计算注意力权重。 for i, hidden_states in enumerate(inputs_embeds): layer = model_layers[i][layer_idx] if hidden_states is None or layer is None: continue hidden_states = layer.input_layernorm(hidden_states) inputs_embeds 是一个包含不同模态输入的列表或张量。例如,它可能包含 VLM 的前缀输入(图像、文本、状态)和 Expert 的后缀输入(动作、时间)。enumerate(inputs_embeds) 会遍历 inputs_embeds 中的每个元素,并返回 i(当前元素的索引)和 hidden_states(对应的输入嵌入)。通过 enumerate 我们可以分别处理每个输入模态,i 用来区分是处理 VLM 还是 Expert。i=0 对应 VLM 的输入,i=1 对应 Expert 的输入。 因此model_layers[i][layer_idx]根据 i 来选择当前是处理 VLM 层还是 Expert 层。如果 i=0,则选择 VLM 的层;如果 i=1,则选择 Expert 的层。layer_idx是当前处理的层的索引,指定当前模型中的哪一层进行处理。 当判断hidden_states is None或layer is None是则跳过不处理,对于Expert侧来说会为空,因为外层是按照VLM层数来遍历的,Expert只有VLM的一半,因此每隔VLM一层就会有一个Expert为空。 先使用input_layernorm对当前输入hidden_states进行归一化。然后就各自进行Q/K/V计算。 hidden_states = hidden_states.to(dtype=layer.self_attn.q_proj.weight.dtype) query_state = layer.self_attn.q_proj(hidden_states).view(hidden_shape) key_state = layer.self_attn.k_proj(hidden_states).view(hidden_shape) value_state = layer.self_attn.v_proj(hidden_states).view(hidden_shape) query_states.append(query_state) key_states.append(key_state) value_states.append(value_state) 在for循环中,遍历VLM和Expert各自计算Q/K/V,然后把VLM和Expert计算的Q/K/V都分类各自加入到相同的列表中,如VLM和Expert的Q加入列表query_states.append。 (2)拼接QKV query_states = torch.cat(query_states, dim=1) key_states = torch.cat(key_states, dim=1) value_states = torch.cat(value_states, dim=1) 将VLM和Expert计算出来的Query、Key、Value各自拼接成一个大的张量,用于后续的注意力计算,从这里可以看出。VLM和Expert的注意力计算是使用一个transformer同时对VLM+Expert的输入拼接输入计算的。相当于VLM和Expert的输入可以双向注意力。 (3)EoPE编码 seq_len = query_states.shape[1] if seq_len < position_ids.shape[1]: _position_ids = position_ids[:, :seq_len] _attention_mask = attention_mask[:, :seq_len, :seq_len] else: _position_ids = position_ids _attention_mask = attention_mask attention_mask_ = _attention_mask position_ids_ = _position_ids query_states = apply_rope(query_states, position_ids_) key_states = apply_rope(key_states, position_ids_) 这段代码主要处理的是位置编码和注意力掩码,这里主要是引入了RoPE编码,计算两个位置之间的相对距离来构造编码,而不是仅仅依赖于绝对位置,提高增强模型的泛化能力。 (4)缓存机制 if use_cache: if fill_kv_cache: past_key_values[layer_idx] = { "key_states": key_states, "value_states": value_states, } else: # TODO here, some optimization can be done - similar to a `StaticCache` we can declare the `max_len` before. # so we create an empty cache, with just one cuda malloc, and if (in autoregressive case) we reach # the max len, then we (for instance) double the cache size. This implementation already exists # in `transformers`. (molbap) key_states = torch.cat([past_key_values[layer_idx]["key_states"], key_states], dim=1) value_states = torch.cat([past_key_values[layer_idx]["value_states"], value_states], dim=1) 将每一层的Key和Value缓存到past_key_values[layer_idx]中,模型训练时这里的use_cache设置为0,当模型是推理时use_cache设置为1,fill_kv_cache设置为1。主要是在推理阶段,会先调用VLM+Expert模型推理一次将Key、Value进行缓存保存起来,后续就只是推理Expert了,VLM将不再计算了,通过这样的方式以提高计算效率。 (5)注意力输出 att_output = attention_interface( attention_mask_, batch_size, head_dim, query_states, key_states, value_states ) return [att_output], past_key_values 注意力计算时会把可用来源(VLM 前缀、Expert 后缀)各自算出的 Q/K/V在序列维度拼接后统一做一次注意力,但掩码保证了“单向可见”,即VLM 与 Expert 的 Q/K/V都参与拼接,但二维掩码使 VLM 基本不看 Expert,Expert 能看 VLM。 交叉注意力 交叉注意力在forward_cross_attn_layer中实现。下面来进行分析。 (1)前缀自注意力 if len(inputs_embeds) == 2 and not past_key_values: seq_len = inputs_embeds[0].shape[1] position_id, expert_position_id = position_ids[:, :seq_len], position_ids[:, seq_len:] prefix_attention_mask = attention_mask[:, :seq_len, :seq_len] layer = model_layers[0][layer_idx] # 选 VLM 的第 layer_idx 层 hidden_states = layer.input_layernorm(inputs_embeds[0]) # 投影出 VLM 的 Q/K/V query_state = layer.self_attn.q_proj(hidden_states).view(B, Lp, H, Dh) key_state = layer.self_attn.k_proj(hidden_states).view(B, Lp, H, Dh) value_state = layer.self_attn.v_proj(hidden_states).view(B, Lp, H, Dh) # 对 Q/K 施加 RoPE(相对位置编码) query_states = apply_rope(query_state, position_id) key_states = apply_rope(key_state, position_id) # 只在 prefix 上自注意力(用 prefix 的方阵 mask) att_output = attention_interface(prefix_attention_mask, batch_size, head_dim, query_states, key_states, value_state) att_outputs.append(att_output) else: expert_position_id = position_ids 当满足inputs_embeds有前缀+后缀的数据且没有缓存的时,只取VLM的输入prefix用于计算自注意力,输出结果为att_outputs。同时如果这层是Expert的交叉注意力,那么VLM计算出来的K/V后面要给到后面Expert用作cross的K/V。 上面前缀自注意力只有只有训练的模型的时候进入交叉注意力每次都会跑,在推理阶段时每次推理只会跑一次。 (2)K/V cache缓存处理 if use_cache and past_key_values is None: past_key_values = {} if use_cache: if fill_kv_cache: past_key_values[layer_idx] = {"key_states": key_states, "value_states": value_states} else: key_states = past_key_values[layer_idx]["key_states"] value_states = past_key_values[layer_idx]["value_states"] 推理的时候会用到缓存,在推理时会调用两次forward。 建缓存阶段(prefix-only):外层会先单独跑一遍,只给 inputs_embeds=[prefix_embs, None],fill_kv_cache=True,把 VLM prefix 的 K/V 存到 past_key_values[layer_idx]。 后缀阶段(真正 cross):用 inputs_embeds=[prefix_embs, suffix_embs] 或者只给 suffix,fill_kv_cache=False,此时直接复用缓存里的 prefix K/V,不用再算。 (3)Expert的交叉注意力 expert_layer = model_layers[1][layer_idx] # 取 Expert 的第 layer_idx 层(可能是 None) if expert_layer is not None: expert_hidden_states = expert_layer.input_layernorm(inputs_embeds[1]) expert_layer is None 的出现是由 get_model_layers 对齐规则决定的,multiple_of = num_vlm_layers // num_expert_layers。Expert要能够计算交叉注意力也要满足当前层是否有Expert层。因为VLM和Expert是对齐的,不一定每一层都有Expert,而当self_attn_every_n_layers设置为2时,相当于是奇数层才会自注意力,而当VLM为16,Expert为8,那么正好Expert都在偶数层基数层没有,所以整个模型都没有注意力机制计算。 expert_query_state = expert_layer.self_attn.q_proj(expert_hidden_states) \ .view(B, Ls, He, Dhe) # 先把 VLM 的 K/V 合并 head 维,变为 [B, Lp, H*Dh] _key_states = key_states.to(dtype=expert_layer.self_attn.k_proj.weight.dtype).view(*key_states.shape[:2], -1) _value_states = value_states.to(dtype=expert_layer.self_attn.v_proj.weight.dtype).view(*value_states.shape[:2], -1) # 再喂给 Expert 自己的 k_proj/v_proj,把维度映射到 Expert 的头数与 head_dim expert_key_states = expert_layer.self_attn.k_proj(_key_states) \ .view(*_key_states.shape[:-1], -1, expert_layer.self_attn.head_dim) # [B, Lp, He, Dhe] expert_value_states = expert_layer.self_attn.v_proj(_value_states) \ .view(*_value_states.shape[:-1], -1, expert_layer.self_attn.head_dim) Expert的expert_query_state来自自己的输入,而expert_key_states、expert_value_states来之与key_states、value_states即为VLM计算过来的缓存K/V。也就是Expert计算注意力是Q使用自己的,而K/V使用的是VLM的。但是需要注意的是可能两边的模型VLM和Expert的hidden宽度、KV头数/维度不一样,先把 VLM K/V 的多头维合并(view(*, H*Dh)),再用 Expert 自己的 k_proj/v_proj 做一次线性变换,映射到 Expert 的多头维度。这就是代码里 “cross K/V 适配层” 的作用;对应到 init,当 attention_mode 包含 "cross" 时,会把 Expert 的 k_proj/v_proj 重定义成输入维=VLM 的 kv_heads x head_dim,输出维=Expert 的。 # 让 Expert 的 token 位置从 0 开始(RoPE 需要相对位置) expert_position_id = expert_position_id - torch.min(expert_position_id, dim=1, keepdim=True).values # 行选择 Expert 的 queries(后缀那段),列只到 prefix 的 K/V 长度(严格 cross,不看自己) expert_attention_mask = attention_mask[:, -inputs_embeds[1].shape[1]:, : expert_key_states.shape[1] ] # 对 Expert 的 Query 施加 RoPE expert_query_states = apply_rope(expert_query_state, expert_position_id) att_output = attention_interface(expert_attention_mask, batch_size, head_dim, expert_query_states, expert_key_states, expert_value_states) att_outputs.append(att_output) 接下来就是计算mask,确保Expert计算cross时只看到前缀(纯cross-attn),不能自回看(不看后缀自身)。再计算RoPE的位置编码,最后调用attention_interface计算交叉注意力得到结果输出。 return att_outputs, past_key_values 最终返回的是两个流对应的自注意力输出,att_outputs 的 长度与 inputs_embeds 对齐,索引0代表VLM 流的输出(前面 prefix 自注意力的结果);索引 1 代表Expert 流的输出(本层 cross 的结果;没有 Expert 就是 None)。外层主循环会据此对两个流分别过 o_proj + 残差 + MLP 等,继续下一层。 总结一下:cross-attn 分支“不拼接 Expert 的 K/V”:Expert 的 Q 只对 VLM 的 K/V(经投影到 Expert 维度)做注意。训练时VLM K/V现场算出并可选择写入缓存;Expert Q 只看这份 VLM K/V。推理时先用前缀阶段填好 VLM KV 缓存;去噪时 Expert Q 直接用缓存的 VLM K/V。VLM 不产生 Q,不会“看”Expert。 Expert要计算交叉注意力需要满足什么条件? 主要看3个参数 L = num_vlm_layers:VLM 总层数 E = num_expert_layers:Expert 总层数(必须 > 0 且能整除 L) S = self_attn_every_n_layers:每隔 S 层强制走一次自注意力(=这层不做 cross) 某层做 cross 的条件 : i % M 0 且(S = 0 或 i % S != 0) 举例1:L=16, E=8;有Expert的层是{0,2,4,6,8,10,12,14},若S=2这些层全是S的倍数,那么没有一层做cross。若S=3,做cross的为{2,4,8,10,14}。 总结一下就是能做cross的,先看每隔几层做cross(间接有self_attn_every_n_layers决定)同时要满足能做cross的这几层有没有Expert。一般情况下,当VLM和Expert具有相同层数是,奇数层做Cross,如果Expert为VLM的一半是需要设置self_attn_every_n_layers设置大于2以上的奇数才能做cross。 层类型 训练时 推理时 Self-Attn VLM & Expert 各自算 QKV → 拼接 → 双向注意 → 切分结果 同训练,但 prefix KV 在首轮缓存,后续复用;双向依旧存在,但 VLM 冻结 Cross-Attn VLM 自注意更新自身 KV;Expert 只算 Q,从 VLM KV(线性投影后)读条件 prefix KV 已缓存;Expert 只算 Q,直接读缓存的 VLM KV;无需重复计算 模型配置 SmolVLAConfig 模型配置主要是SmolVLAConfig类,其决定了训练/推理是模型结构、预处理、优化器/调度器、以及VLM骨干选择与冻结策略。 class SmolVLAConfig(PreTrainedConfig): # Input / output structure. n_obs_steps: int = 1 chunk_size: int = 50 n_action_steps: int = 50 normalization_mapping: dict[str, NormalizationMode] = field( default_factory=lambda: { "VISUAL": NormalizationMode.IDENTITY, "STATE": NormalizationMode.MEAN_STD, "ACTION": NormalizationMode.MEAN_STD, } ) # Shorter state and action vectors will be padded max_state_dim: int = 32 max_action_dim: int = 32 # Image preprocessing resize_imgs_with_padding: tuple[int, int] = (512, 512) # Add empty images. Used by smolvla_aloha_sim which adds the empty # left and right wrist cameras in addition to the top camera. empty_cameras: int = 0 # Converts the joint and gripper values from the standard Aloha space to # the space used by the pi internal runtime which was used to train the base model. adapt_to_pi_aloha: bool = False # Converts joint dimensions to deltas with respect to the current state before passing to the model. # Gripper dimensions will remain in absolute values. use_delta_joint_actions_aloha: bool = False # Tokenizer tokenizer_max_length: int = 48 # Decoding num_steps: int = 10 # Attention utils use_cache: bool = True # Finetuning settings freeze_vision_encoder: bool = True train_expert_only: bool = True train_state_proj: bool = True # Training presets optimizer_lr: float = 1e-4 optimizer_betas: tuple[float, float] = (0.9, 0.95) optimizer_eps: float = 1e-8 optimizer_weight_decay: float = 1e-10 optimizer_grad_clip_norm: float = 10 scheduler_warmup_steps: int = 1_000 scheduler_decay_steps: int = 30_000 scheduler_decay_lr: float = 2.5e-6 vlm_model_name: str = "HuggingFaceTB/SmolVLM2-500M-Video-Instruct" # Select the VLM backbone. load_vlm_weights: bool = False # Set to True in case of training the expert from scratch. True when init from pretrained SmolVLA weights add_image_special_tokens: bool = False # Whether to use special image tokens around image features. attention_mode: str = "cross_attn" prefix_length: int = -1 pad_language_to: str = "longest" # "max_length" num_expert_layers: int = 8 # Less or equal to 0 is the default where the action expert has the same number of layers of VLM. Otherwise the expert have less layers. num_vlm_layers: int = 16 # Number of layers used in the VLM (first num_vlm_layers layers) self_attn_every_n_layers: int = 2 # Interleave SA layers each self_attn_every_n_layers expert_width_multiplier: float = 0.75 # The action expert hidden size (wrt to the VLM) min_period: float = 4e-3 # sensitivity range for the timestep used in sine-cosine positional encoding max_period: float = 4.0 可以分为几个部分 (1)输入输出与时序 n_obs_steps: 输入观测的历史步数,默认为1。 chunk_size:每次模型生成的动作序列长度(后缀序列长度)。 n_action_steps:外部消费的动作步数,需要满足n_action_steps <= chunk_size(代码中已校验)。 采样与训练的后缀长度在 VLAFlowMatching.sample_actions/forward 中使用,动作队列在 SmolVLAPolicy 中按 n_action_steps 出队。 (2)归一化与特征维度 normalization_mapping:各模态的标准化策略,视觉默认 Identity,状态与动作 MeanStd。 max_state_dim/max_action_dim:状态、动作向量的固定上限维度;短向量会 pad 到该维度(pad_vector)。 Normalize/Unnormalize 与 state_proj/action_ x _proj 的投影维度。 (3)图像预处理与空相机 resize_imgs_with_padding=(512,512):视觉输入 pad-resize 到固定分辨率,然后再做 [-1,1] 归一化(SigLIP 习惯)。 empty_cameras:允许在 batch 缺少图像时补空相机占位(用于多摄像头但部分缺失的场景)。 (4)Aloha 相关开关 adapt_to_pi_aloha:状态/动作与 Aloha 空间的双向转换(关节翻转、夹爪角度/线性空间互转)。 use_delta_joint_actions_aloha:将关节维度转为相对量(目前未在 LeRobot 中实现,置 True 会报错)。 (5)文本与采样步数 tokenizer_max_length=48:语言 token 最大长度。 num_steps=10:Flow Matching 反推理的 Euler 步数(越大越精细,越慢)。 prepare_language、sample_actions 的迭代去噪循环。 (6)缓存与注意力 use_cache=True:是否使用 KV-Cache(前缀只算一次,后续重复用)。 attention_mode="cross_attn":与 SmolVLMWithExpertModel 的交叉注意力对齐策略。 prefix_length=-1/pad_language_to="longest":前缀长度/语言 padding 策略;用于构造 attention_mask 与 position_ids。 (7)微调的策略 freeze_vision_encoder=True:冻结 VLM 视觉编码器。 train_expert_only=True:只训练动作 expert(VLM 其它部分冻结)。 train_state_proj=True:是否训练状态投影层。 影响SmolVLMWithExpertModel.set_requires_grad 以及 VLM 参数的 requires_grad 设置。 (8)优化器与调度器 optimizer_* 与 scheduler_*:在训练入口 TrainPipelineConfig.validate() 使用,生成默认的 AdamW + 余弦退火带预热调度。 可被 CLI 覆写(如 --optimizer.lr 等)。 (9)VLM骨干与权重加载 vlm_model_name="HuggingFaceTB/SmolVLM2-500M-Video-Instruct":指定用哪个 VLM 仓库(用于取 tokenizer/processor,和构建骨干结构)。 load_vlm_weights=False:是否直接从该 VLM 仓库下载骨干权重。为 False时只拿 AutoConfig 构结构,权重随机初始化,随后通常被策略检查点覆盖。为 True时用 AutoModelForImageTextToText.from_pretrained 加载骨干权重(仅在 --policy.type=smolvla 路线下常用)。 与 --policy.path 的关系为用 --policy.path=lerobot/smolvla_base 时,实际权重来自本地/Hub 的策略检查点(包含 VLM+expert),不会使用骨干权重,但仍会用 vlm_model_name 主要是加载 tokenizer/processor。用 --policy.type=smolvla 时,vlm_model_name 决定骨干结构,load_vlm_weights 决定是否拉骨干权重,expert 按本地配置新建训练。 (10)层数与宽度对齐 num_vlm_layers:把 VLM 的文本层裁剪为前 N 层再用。裁剪层数后设为 self.num_vlm_layers。 num_expert_layers:专家 expert 模型的层数;若 ≤0 则默认与 VLM 层数相同。决定 expert 与 VLM 的层对齐步长 multiple_of = num_vlm_layers // num_expert_layers。只有在 i % multiple_of = 0 的 VLM 层位点才映射到一个 expert 层用于交叉注意力;其他层的 expert_layer 为空。 self_attn_every_n_layers:每隔 n 层强制走“仅自注意力”而不是交叉注意力。当 attention_mode 含 “cross” 且 fill_kv_cache=False 时,如果 layer_idx % n = 0 则走 self-attn 分支,否则走 cross-attn 分支。例如n=2 → 偶数层自注意、奇数层尝试交叉注意,但还需该层“有映射到的 expert 层”(见 multiple_of)才真正执行 cross-attn。 expert_width_multiplier:expert 的隐藏维度 = VLM 隐藏维度 × multiplier(同时重设 FFN 的 intermediate_size)。expert 更窄以降算力;但会改动线性层形状,需与加载的检查点一致,否则会维度不匹配。为实现 cross-attn,代码会按 VLM hidden 尺寸重建部分 q/k/v 投影,使其能接收来自 VLM 的输入(跳过“只自注意”层)。 在SmolVLAConfig配置集中定义了 SmolVLA 的“结构与训练/推理开关”。训练微调常用 --policy.path=lerobot/smolvla_base,此时多数结构参数不宜修改,微调时从smolvla_base中加载config.json配置;而从骨干自建训练时才需要精细调 num_expert_layers/num_vlm_layers/expert_width_multiplier/load_vlm_weights 等,并确保与骨干 hidden_size/层数一致。 加载流程 策略的加载主要分为两条入口路径,两者互斥,通过启动时参数指定。 (1)--policy.path=....方式 用 --policy.path=.....:指定一个已存在的策略checkpoint(Hub 上或本地目录)。如训练时微调可以指定lerobot/smolvla_base,推理时指定output/train/pretrained_model。会从 path/config.json 里反序列化成 SmolVLAConfig;会加载同目录下的 model.safetensors(整个策略权重:VLM骨干 + 动作专家 + 投影层等);训练开始时,模型已经有了一套完整的初始化参数(通常是预训练好的)。 python -m lerobot.scripts.train \ --policy.path=lerobot/smolvla_base \ --dataset.repo_id=xxx \ --batch_size=64 --steps=200000 这里会拿 Hugging Face Hub 上的 lerobot/smolvla_base(含 config.json + model.safetensors,整个策略权重:VLM骨干 + 动作专家 + 投影层等)来初始化。 (2)--policy.type=smolvla方式 指定一个 策略类别(由 @PreTrainedConfig.register_subclass("smolvla") 注册)。会创建一个全新的 SmolVLAConfig 对象(带默认超参),而不是加载 checkpoint。没有预训练权重,除非配合 load_vlm_weights=True,这时只会拉取纯VLM背骨的预训练权重(而动作专家层仍然是随机初始化)。可以用命令行参数覆盖任意超参(比如 --policy.num_expert_layers=4)。 python -m lerobot.scripts.train \ --policy.type=smolvla \ --dataset.repo_id=xxx \ --batch_size=64 --steps=200000 \ --policy.load_vlm_weights=True 从零(或仅用 VLM 预训练骨干)开始训练一个新策略。 下面以推理和训练举例说明其调用流程。 (1)训练使用policy.path方式 在 validate() 中读取 path,并把所有 --policy.xxx 作为“同层覆写”传入配置加载。 policy_path = parser.get_path_arg("policy") self.policy = PreTrainedConfig.from_pretrained(policy_path, cli_overrides=cli_overrides) self.policy.pretrained_path = policy_path 判断是从本地目录还是Hub下载获取配置文件,然后应用得到 SmolVLAConfig。只加载“配置”(config.json),不加载模型权重。权重加载发生在后续 policy_cls.from_pretrained(...)(另一个类,见 policies/pretrained.py)。 @classmethod def from_pretrained(cls, pretrained_name_or_path, *, ..., **policy_kwargs) -> T: model_id = str(pretrained_name_or_path) # 1) 决定从本地目录还是Hub取配置文件(只取config,不取权重) if Path(model_id).is_dir(): if CONFIG_NAME in os.listdir(model_id): config_file = os.path.join(model_id, CONFIG_NAME) else: print(f"{CONFIG_NAME} not found in {Path(model_id).resolve()}") else: try: config_file = hf_hub_download(repo_id=model_id, filename=CONFIG_NAME, ...) except HfHubHTTPError as e: raise FileNotFoundError(...) from e # 2) 应用CLI覆写(如 --policy.xxx=...) cli_overrides = policy_kwargs.pop("cli_overrides", []) with draccus.config_type("json"): return draccus.parse(cls, config_file, args=cli_overrides) 构建策略,注入数据集特征与统计,若存在 pretrained_path 则连同权重加载。 cfg.input_features/output_features = ... if cfg.pretrained_path: policy = policy_cls.from_pretrained(**kwargs) else: policy = policy_cls(**kwargs) 加载权重(目录或 Hub 的 model.safetensors),随后迁移到 device、设 eval()(训练循环里会再切回 train())。 if os.path.isdir(model_id): policy = cls._load_as_safetensor(...) policy.to(config.device); policy.eval() SmolVLA 特定初始化,即使走 path,仍按 vlm_model_name 加载 tokenizer/processor(非权重),并实例化骨干+expert。 self.language_tokenizer = AutoProcessor.from_pretrained(self.config.vlm_model_name).tokenizer self.model = VLAFlowMatching(config) (2)训练使用policy.type方式 draccus 按类型直接实例化 SmolVLAConfig(该类已注册)并解析 --policy.xxx。 @PreTrainedConfig.register_subclass("smolvla") class SmolVLAConfig(PreTrainedConfig): make_policy 同上;因无 pretrained_path,默认从零构建。若配置 load_vlm_weights=true,才会把骨干权重从 vlm_model_name 拉下来(expert 仍需训练)。 if load_vlm_weights: self.vlm = AutoModelForImageTextToText.from_pretrained(model_id, ...) else: config = AutoConfig.from_pretrained(model_id) self.vlm = SmolVLMForConditionalGeneration(config=config) (3)推理模式只能使用policy.path方式 policy_path = parser.get_path_arg("policy") self.policy = PreTrainedConfig.from_pretrained(policy_path, cli_overrides=cli_overrides) self.policy.pretrained_path = policy_path record 的配置按policy.path加载训练的模型,随后通过 predict_action/select_action 使用策略进行推理。 policy.path 对比 policy.type 维度 policy.path=... policy.type=smolvla 配置来源 从 checkpoint 目录/Hub 仓库里的 config.json 反序列化成 SmolVLAConfig 通过 @PreTrainedConfig.register_subclass("smolvla") 新建一个默认 SmolVLAConfig,命令行可覆写 权重来源 从 checkpoint 里的 model.safetensors 加载完整策略权重(VLM骨干 + 动作专家 + 投影层) 默认全随机;若 load_vlm_weights=True,则只加载 VLM骨干权重(SmolVLM2),动作专家仍随机 归一化统计 不从 checkpoint 恢复,而是来自数据集 dataset_stats(normalize_inputs/targets在加载时被忽略) 同左 Tokenizer/Processor 仍然会用 config.vlm_model_name(默认 HuggingFaceTB/SmolVLM2)加载 tokenizer/processor 同左 常见场景 - 直接推理- 微调已有策略 - 从零开始训练新策略- 换结构做实验(改 num_expert_layers、expert_width_multiplier等) 推理可用性 一键可用(权重完整) 不可直接用(专家没训练,输出无意义),除非后续手动加载你自己训练好的权重 是否需要 HuggingFaceTB/SmolVLM2 权重 不需要(只用到它的 processor/tokenizer) 如果 load_vlm_weights=True → 需要拉骨干权重;否则全随机 -
从数学角度理解flow matching中的线性插值
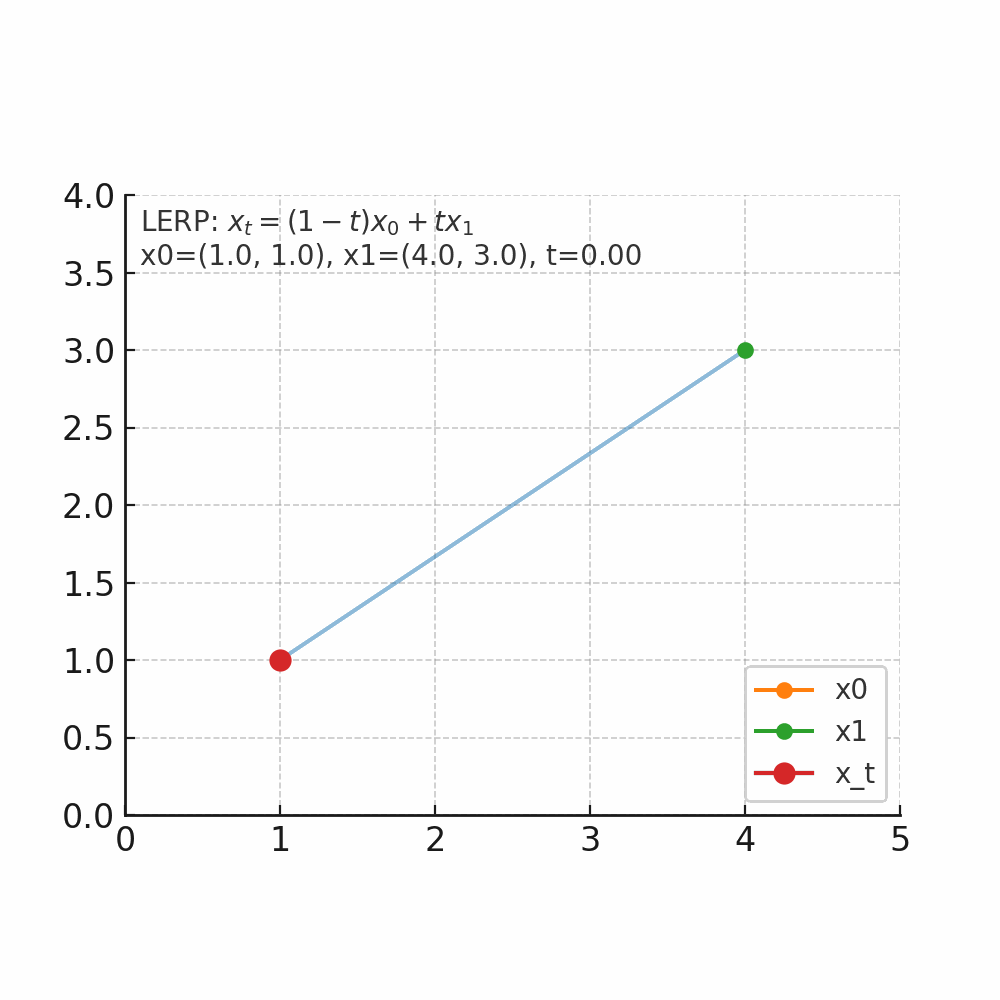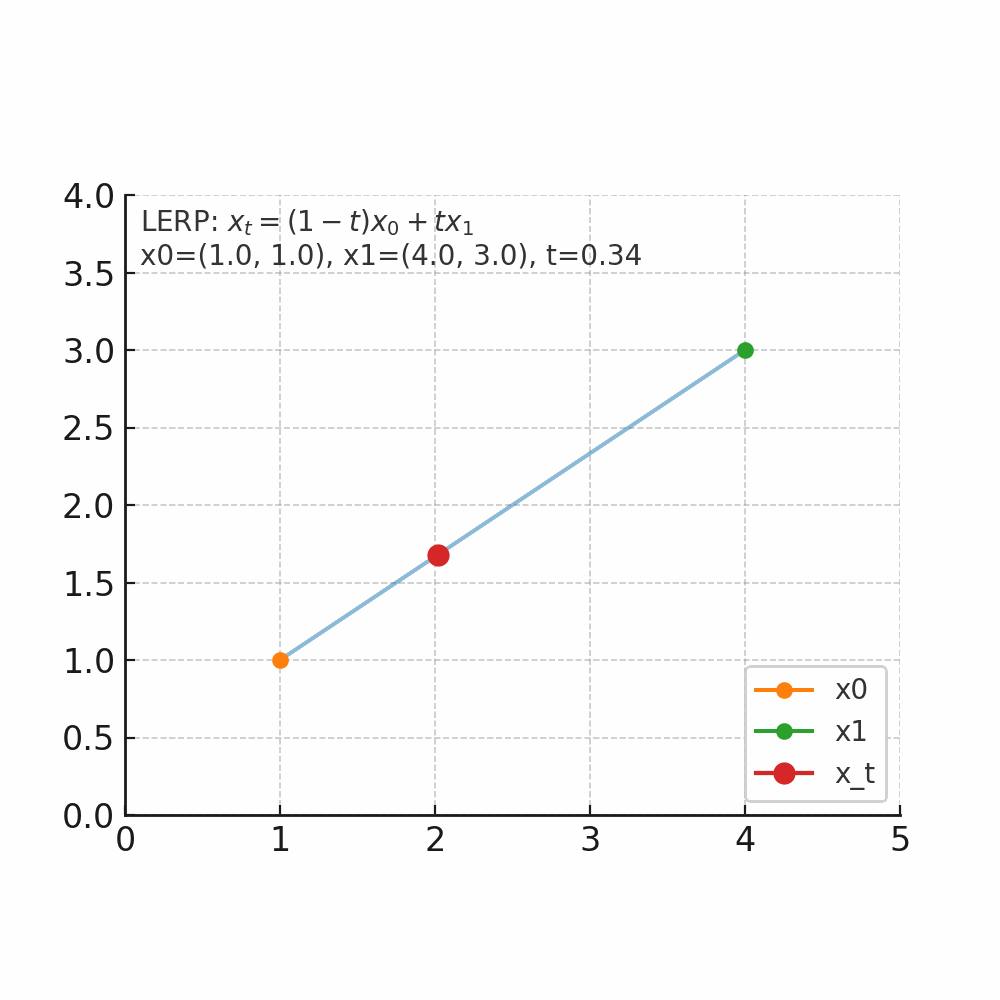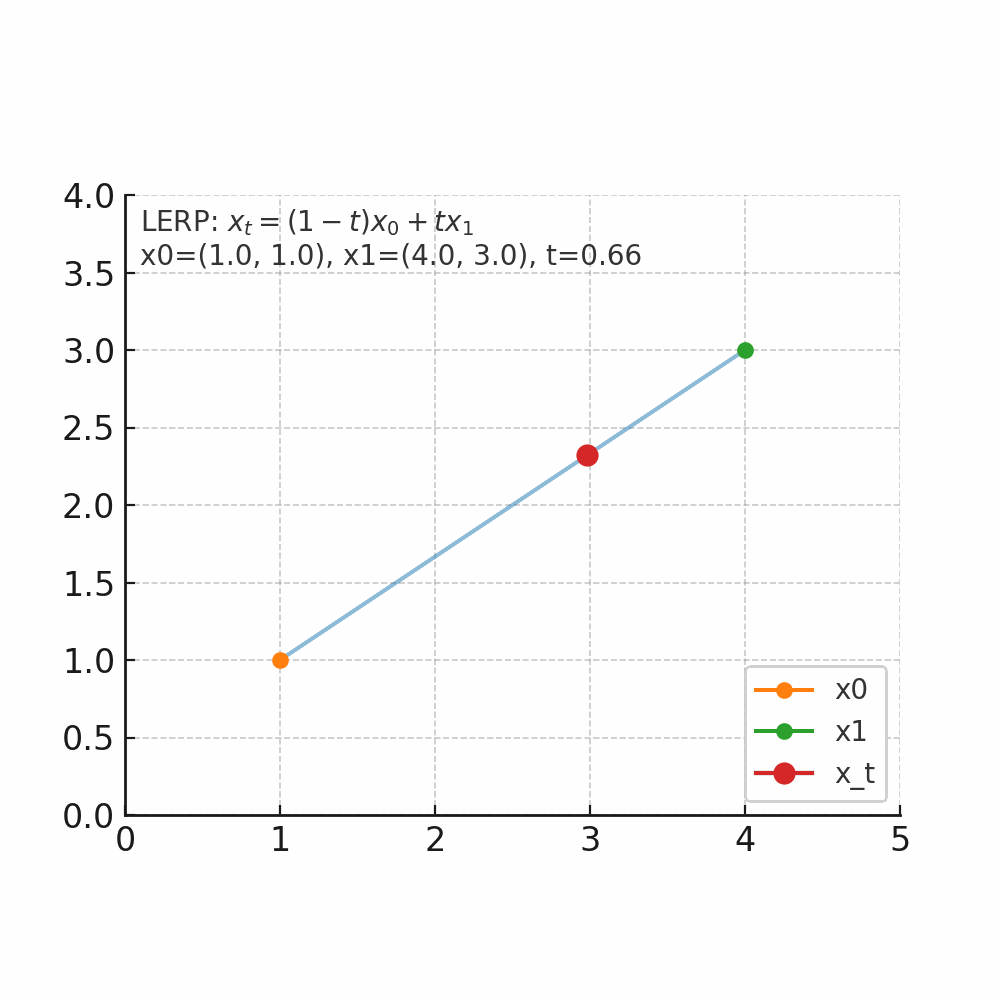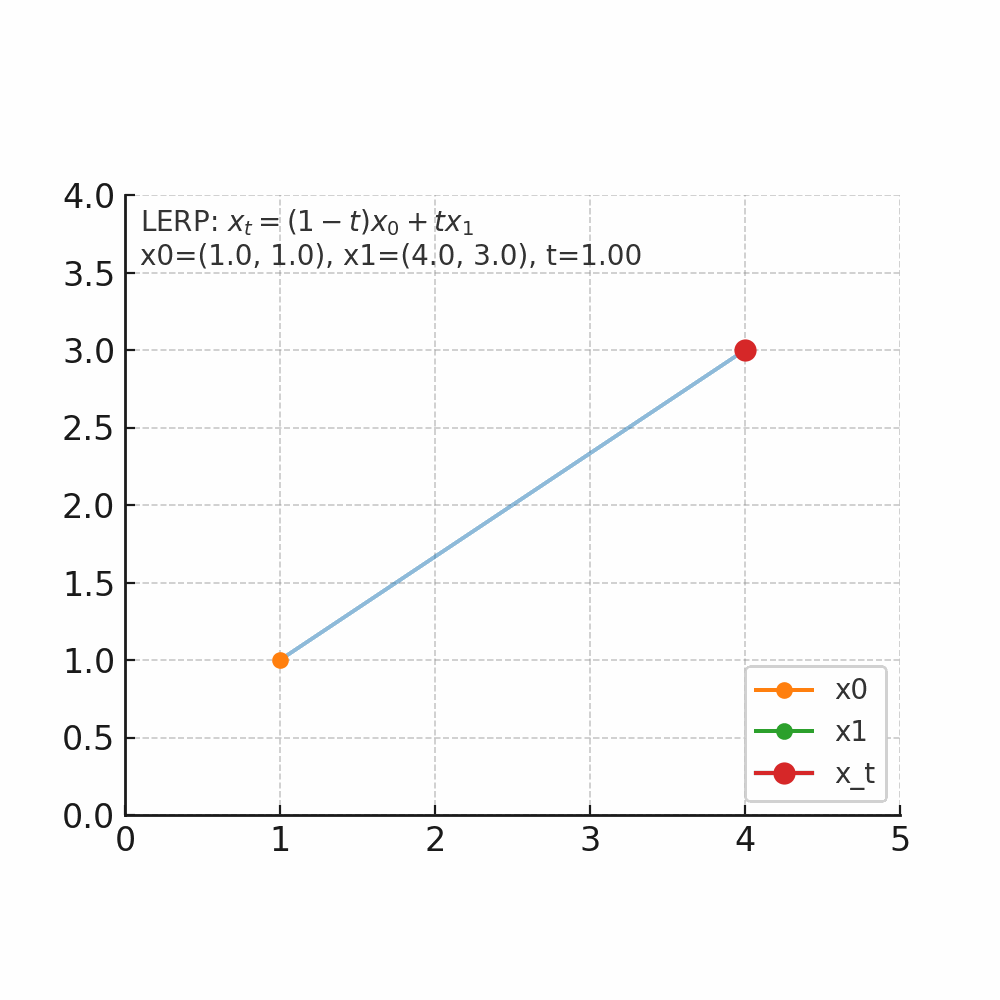
什么是插值 插值的核心问题是:在已知两个点的情况下,如何找到它们之间的中间点。 举个人走路的例子,起点在家门口(A点),终点在公司(B点),总的路程为1000米,假设人是匀速移动,如果走到一半(t=0.5),那么人就在家和公司的正中间,如果走到四分之一(t=0.25),那么离家250米,离公司750米。 线性插值(LERP) 是最简单的一种:它假设两个点之间的变化是“直线型、匀速”的。 公式 $$ x_t = (1-t)x_0 + t x_1, \quad t \in [0,1] $$ 把两个量$x_0$和$x_1$按加权$1-t$与$t$做加权平均,得到他们之间的线性过渡点。$x_0$是起点,$x_1$是终点,$t$是插值因子,控制起点与重点的位置。当 $t=0$,结果是 $x_0$;当 $t=1$,结果是 $x_1$;当 $t=0.5$,结果是中点;$t$从0到1连续变化时,$x_t$沿着二者之间等速变化(为什么是等速,待会解释)。 先上个图看看直观体会一下。 如图所示起点$x_0$为坐标(1,1),终点$x_1$(4,3),当$t$从0开始连续变化是,$x_t$的位置会朝着$x_1$的方向变化。 当$t=0$时,坐标为(1 - 0) x (1, 1) + 0 x (4, 3) = (1, 1)。 当$t=0.2$时,坐标为(1 - 0.2) x (1, 1) + 0.2 x (4, 3) = (1.6, 1.4)。 当$t=0.5$时,坐标为(1 - 0.5) x (1, 1) + 0.5 x (4, 3) = (2.5, 2)。 当$t=1$时,坐标为(1 - 01) x (1, 1) + 1 x (4, 3) = (4, 3)。 通过公式可以算出每个时间的位置,但是如果要知道每个位置变化的速度/趋势我们应该怎么来衡量了? 那自然就是要求导数了。 $$ \frac{d}{dt}x_t = x_1 - x_0 $$ 可以看到其倒数是一个常数,那就意味着变化是匀速的,以上图为例,都是朝着(4,3)-(1,1)=(3,2)的向量方向去变化。 有了这个变化量,假设我们时间步$\Delta t=0.1$,那么意味着每次变化的位置是0.1 x (3,2) = (0.3, 0.2);假设当前位置是(1,1)那么就可以计算出下一个时间步的位置为$(1,1)+(0.3,0.2)=(1.3,0.2)$。这就与我们此前flow matching里面的公式$x_{k+1} = x_k + v_\theta(x_k, t_k)\Delta t$。 -
轻量SmolVLA:半层VLM、视觉压缩与异步推理赋能具身智能
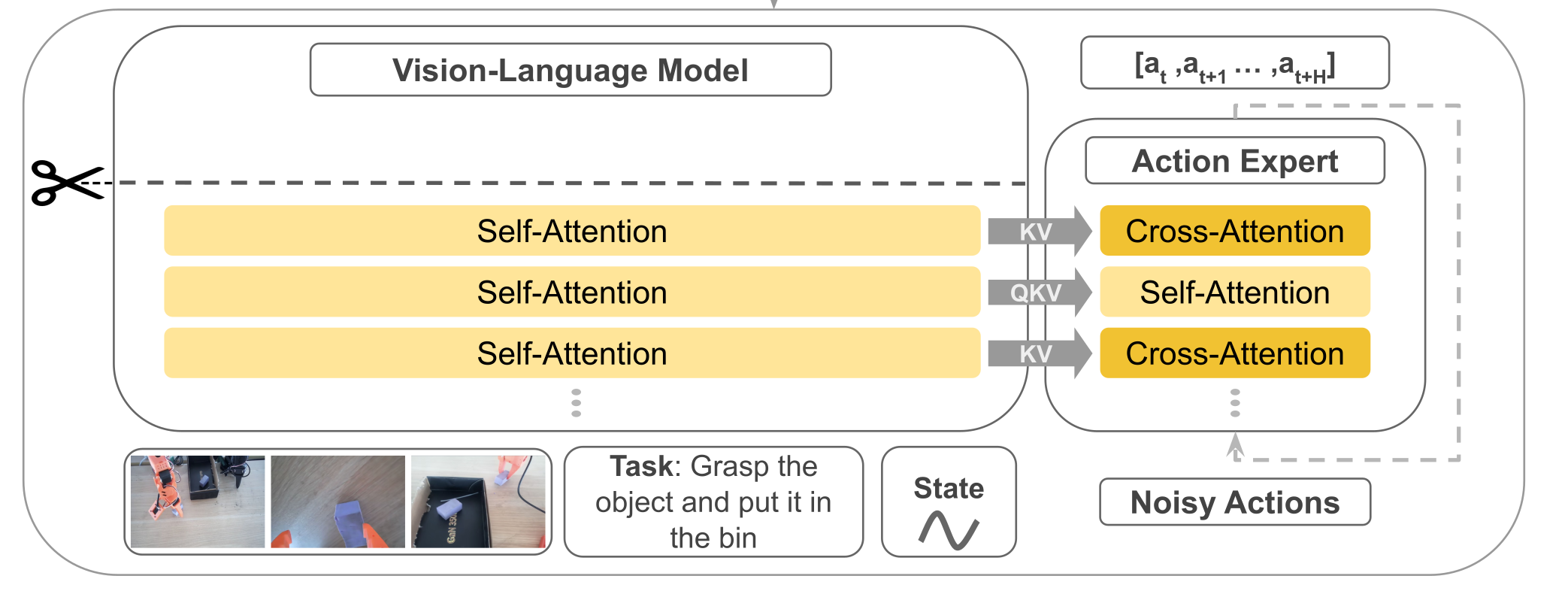
概述 SmolVLA 是一套轻量级视觉-语言-行动(VLA)策略:前端用小型 VLM(视觉 SigLIP + 语言 SmolLM2)做感知与理解;后端用一个“动作专家”专门预测一段连续的低层控制。它与Pi0相比,参数规模少了将近10倍只有约0.45B(450M)。它的目标是在低算力下也能稳定执行多任务机器人控制,并保持接近甚至超过更大模型的效果。 SmolVLA 通过冻结 VLM、只训练动作专家(Action Expert),再配上四件“硬核小技巧”——取 VLM 的前半层、把每帧视觉 token 压到 64、以及Self-Attn—>Cross-Attn交替方式、异步推理;在大幅降算力与时延的同时,保持/逼近甚至超过更大模型的性能;注意力计算交替方式让动作专家既能不断获取外部视觉/语言指导,又能在内部序列里建立自己的时序与物理一致性,从而在算力可控的前提下提升稳定性和表现;提供异步执行,把“算下一段动作”和“执行当前动作”并行起来,显著减少空窗时间。 原理 结构 其模型结构主要有前端的VLM+后端的动作专家Action Expert组成,结构组成与Pi基本一致但实现方式有很大差异不同。先总结一下组件,稍后我们在稍作展开补充。 输入:文本指令token+视觉token(多摄像头采集的图像)+机器的状态(关节角、传感器)。 VLM(感知端):采用SmolVLM-2,VLM共有L层,但是只N=⌊L/2⌋层隐藏表示喂给动作专家。 Action Expert(控制端):一个Flow Matching Transformer,以以Cross → Causal Self → Cross 的“三明治”层为基本单元,按块预测n步动作序列。 输出:一次预测长度为n的动作块,对应机器的控制指令。 SmolVLA与Pi0有很多相似之处,不过其背后有四个关键设计,分别是Layer Skipping(层跳过)、Visual tokens reduction(视觉token压缩)、动作专家交替Self-Attn与Cross-Attn、异步推理。本小节先围绕前面3部分进行解析,异步推理于后续章节展开。 (1)Layer Skipping 层跳过就是把感知端的VLM(视觉+语言)的解码器中间层拿来当条件特征,而不是等它把整个层都计算完再输出;具体的做法就是只去$N=L/2$层的隐藏层表示送给动作专家,VLM权重冻结不训练。之所以要这样做经验规律表示(论文中作者提到)深层 LLM 层更偏“词级生成/长链路语义”,而中层已经集中了“指令 + 视觉”的对齐语义,对控制足够;继续往后让语言头生成 token 既耗算,又不是控制必须。前半层就停下,少算一半的自注意 + MLP,显存开销也随之下降。 大概得实现是把“文本指令 token、图像 token、状态 token”拼接,送入解码器;在第$N$层获取特征信息H然后用一个线性投影到Action expert所需的维度$d_a$作为$K/V$。如果在长时、极强推理型任务(需要深层语言生成)时可以适当调大N。 (2)视觉token压缩 在transformer里面,“token”就是序列里的一个位置。对图像来说,我们把一张图拆成很多小块(patch)或网格上的特征点,每个块/点用一个向量表示,这个向量就是视觉 token(不明白的可以看看ViT原理解析介绍)。视觉token压缩具体的做法是保整图、不裁块,把空间上密的token折叠到通道里,从而让token数变少。 设 ViT patch 后得到的特征图大小为 $\frac{H}{p} \times \frac{W}{p} \times d$,选一个下采样因子 $r$ (整数),做 space-to-depth: $$ \underbrace{\frac{H}{p} \times \frac{W}{p}}{\text{原网格}} \xrightarrow{\div r} \underbrace{\frac{H}{pr} \times \frac{W}{pr}}{\text{更稀疏的网格}}, \quad \underbrace{d}{\text{通道}} \xrightarrow{\times r^2} \underbrace{d \cdot r^2}{\text{更厚的通道}} $$ 计算示例: 输入尺寸:$512 \times 512$ 图像 Patch大小 $p=16$ ⇒ $32 \times 32$ token网格 选$r=4$ ⇒ $\frac{32}{4} \times \frac{32}{4} = 8 \times 8$ 网格 Token数:$8 \times 8 = 64$(减少$4^2=16$倍) 通道维度:$d=3 \rightarrow d=3 \times 16=48$ 可以看到如果是按照ViT的默认方式patch数量为32x32=1024,每个patch的维度为3x16x16=768,然后如果输入编码的$d_mode=512$那么经过线性投影变成矩阵(1024,512),即1024个token数量,每个token维度是512;而如果进行压缩后patch数量为8x8=64,每个patch的维度为48x16x16=12288,经过线性投影后变成(64,512)即64个token,每个维度是512。这里也可以看到原来是768降为到512,压缩的是从12288降维到512,降得比较猛,效果真的没有衰减吗? 总结一下smolvla在视觉token上进行了压缩,使用space-to-depth,对于512X512的图每帧token从1024降低到了64帧,如ViT的patch操作后得到的特征图维度为$\mathbb{R}^{\frac{H}{p} \times \frac{W}{p} \times d}$,选择下采样因子 $r$(整数)进行space-to-depth操作: $$ \mathbb{R}^{\frac{H}{p}\times\frac{W}{p}\times d} \xrightarrow{\text{S2D}_{r}} \mathbb{R}^{\frac{H}{pr}\times\frac{W}{pr}\times(d\cdot r^{2})} $$ 这样token数减少$r^{2}$倍,把细节挪到通道数去。 (3)动作专家交替Self-Attn与Cross-Attn 在动作专家中使用了交叉注意力机制,具体的排布可以配置。VLM的每一层与右边的Expert是一一对齐的,当然也可以配置Expert模型只有VLM层数的一半,每两层VLM才有一层Expert,那么其中VLM对齐层将为NONE,下图以VLM和Expert都为4层来示例交替注意力的实现。 Self-Attn(管自己,守时序):只允许第 i 步看 ≤i 的历史步(因果掩码),在动作序列内部传播动力学与约束,做轨迹的时间一致性与平滑。这一步相当于“内化刚才读到的证据”并让各步动作彼此协调。在计算注意力时,会将VLM的QKV与Expert的QKV进行拼接起来一起送入transformer计算,但通过掩码保证 VLM 的Q只看自己(不去读 Expert),而 Expert 的 Q 可以访问 VLM 的 K/V(即“读”VLM 语义),这样既提供了计算效率也提升了Expert的语义丰富性。 Cross-Attn(看环境,取证):看环境取证,让每个动作 token 先从条件特征里“读”一遍(条件=VLM中间层输出,含文本指令+多路视觉+状态)。这样动作表示一开始就被场景锚定,知道当下该关注哪里/哪件物体。具体是交叉注意力计算Q来自Expert Action自己,而K/V 来自 VLM 对应层的输出缓存。 训练 目标让动作专家 在观测条件 $o_t$ 下输出$v_\theta$速度场,把“噪声动作”沿路径推向真实动作块 $A_t$。这里跟Pi0和Flow Matching是一样大同小异,就简要说明一下。 观测条件:$o_t=H^{(N)}\in\mathbb{R}^{T\times d_o}\ \xrightarrow{\text{proj}}\ O_N\in\mathbb{R}^{T\times d_a}$(VLM 冻结;$O_N$ 作为 Cross-Attn 的 K/V)。 真实动作块:$A_t\in\mathbb{R}^{n\times d_{\text{act}}}$(建议标准化/白化)。 噪声:$\varepsilon\sim\mathcal N(0,I)$(同形)。 路径时间:$\tau\sim\mathrm{Beta}(\alpha,\beta)$。这里与Pi0不同。 路径与目标速度场: $$ A_t^{\tau}=\tau A_t+(1-\tau)\varepsilon,\left(A_t^{\tau}\mid A_t\right)=\varepsilon-A_t $$ 计算损失函数: $$ \mathcal{L}^{\tau}(\theta) = \mathbb{E}{p\left(\mathbf{A}{t} \mid \mathbf{o}{t}\right), q\left(\mathbf{A}{t}^{\tau} \mid \mathbf{A}{t}\right)} \left[ \left|| \mathbf{v}{\theta}\left(\mathbf{A}{t}^{\tau}, \mathbf{o}{t}\right) - \mathbf{u}\left(\mathbf{A}{t}^{\tau} \mid \mathbf{A}{t}\right) \right||^{2} \right] $$ 这里 $||\cdot||^{2}$ 表示欧氏范数平方;实现即逐元素 MSE。 为提升推理效率,动作专家隐藏宽度取 $d_a=0.75\times d$($d$ 为 VLM 的隐藏宽度)。 以下是一个简单的示例,可看看过程理解一下。 # 条件:取 VLM 第 N 层隐藏(冻结) with torch.no_grad(): H = vlm_hidden_at_layer_N(obs_tokens) # [T, d_o] KV = proj(H) # [T, d_a] 供 Cross-Attn 作 K/V(可缓存) # 构造路径与目标速度 A = sample_action_chunk() # [n, d_act] (已标准化) eps = torch.randn_like(A) # [n, d_act] tau = Beta(alpha, beta).sample(()).to(A.device) A_tau = tau * A + (1 - tau) * eps u = eps - A # 前向与损失 pred = v_theta(A_tau, KV) # 与 u 同形 loss = F.mse_loss(pred, u) # 对应 ||·||^2 loss.backward(); optimizer.step(); optimizer.zero_grad() 推理 在SmolVLA提到了异步推理,先来看看同步推理。 取最新观测 → 得到 $O_N$; 以噪声初始化,做 $K\approx10$ 步显式积分(Euler/Heun)得到一个动作块 $[a_t,\dots,a_{t+n-1}]$; 执行动作块 → 重复。 同步(sync)推理一次性生成长度为 $n$ 的动作队列(chunk)$A_t=\big[a_t,\dots,a_{t+n-1}\big]$,执行完再用新观测预测下一段。执行与推理串行,会产生“空窗”(执行停下等待推理)。而异步(async)推理是解耦“动作执行”和“动作预测”。机器人端持续消费现有队列;当队列余额低于阈值就异步把当前观测发给策略端预测“下一段”,回来后与旧队列重叠拼接。这样执行与推理并行,显著降低总时延,同时仍保持接近的成功率。 异步推理在架构上可以分为两个部分: RobotClient(机器人端):以控制周期 $\Delta t$ 持续下发队列头部动作;本地维护动作队列 $A_t$ 与触发逻辑;可做相似度过滤(见下节)。 PolicyServer(策略端):接收观测 $o_t$,运行策略 $\pi$ 预测新队列 $\tilde A_{t+1}$ 后返回;可放在更强的远端算力(GPU/工作站/云)。 看看论文中给出的算法实现: 设时域 $T$、段长 $n$、触发阈值 $g\in[0,1]$。 初始化:采集 $o_0$,发送到策略端,得到首段 $A_0\leftarrow\pi(o_0)$。 主循环 对 $t=0\dots T$:取出并执行一步 $a_t\leftarrow\text{PopFront}(A_t)$;若 队列余额占比 $\dfrac{|A_t|}{n}<g$,采集新观测 $o_{t+1}$;若 NeedsProcessing$(o_{t+1})$ 为真(见“相似度过滤”),则异步触发:①发送 $o_{t+1}$ 到策略端,得到新段 $\tilde A_{t+1}\leftarrow\pi(o_{t+1})$(异步返回);②用重叠拼接函数 $f(\cdot)$ 合并:$A_{t+1}\leftarrow f(A_t,\tilde A_{t+1})$;若本轮异步推理尚未结束:$A_{t+1}\leftarrow A_t$(继续消费旧队列)。 论文中的 NeedsProcessing 用于避免重复观测触发;$f$ 表示对重叠步的拼接(线性渐入/平滑器等,见下重叠拼接(Overlap & Merge))。 关键触发量,队列余额阈值 $g$: 触发条件:当 $\dfrac{|A_t|}{n}<g$ 时触发一次异步预测。 直觉:$g$ 越大,越提前触发,越不容易见底;但也会更频繁地调用策略端(算力/网络开销更高)。 论文的三个代表场景:$g=0$(顺序极限):耗尽队列才发起新预测 → 一定出现空窗等待;$g=0.7$(典型异步):每段大约消耗 $1-g=0.3$ 的比例就触发,计算摊在执行过程中,队列不见底;$g=1$(计算密集极限):步步都发观测 → 几乎“满队列”,反应最快但计算最贵(等同每个 tick 都前向一次)。 对于相似性过滤做法:主要动机是观测几乎不变时没必要反复调用服务器 → 降低抖动与无效请求。具体做法(论文)是用关节空间距离作为近似(例如欧式距离),若两次观测间距离 $<\varepsilon$(阈值,$\varepsilon\in\mathbb{R}^+$)则丢弃本次请求。兜底做法是若队列真的耗尽,则无论相似度如何都要处理最近的观测,以防停摆。 重叠拼接(Overlap & Merge):核心思想通过重叠区域平滑过渡避免硬切抖动,数学上实现是设旧队列尾部与新队列头部重叠 $w$ 步,对第 $k=0,\dots,w-1$ 步做线性渐入融合: $$ a_{t+k}^{\text{merge}} = \alpha_k \tilde{a}{t+1+k} + (1-\alpha_k) a{t+k}, \quad \alpha_k = \frac{k+1}{w} $$ 也可用余弦窗、Slerp 或在位姿/速度层加滤波器;关键是重叠 + 平滑避免硬切抖动。 总结一下对于异步并发处理有优势,但是需要处理其中的细节主要是: 维护动作队列。前台执行当前队列,后台异步预测下一段;在重叠窗口内平滑拼接新旧段。 避免队列见底的解析下界,设控制周期为 $\Delta t$,则避免队列耗尽的充分条件为 $$ g\ \ge\ \frac{\mathbb E[\ell_S]/\Delta t}{n} $$ 其中 $\ell_S$ 为一次(本地/远端)推理延迟,$\Delta t$ 控制周期,$n$ 为动作块长度。从触发到返回的时间内(平均 $\mathbb{E}[\ell_S]$ 秒)你还要有足够的剩余动作可执行(约 $\mathbb{E}[\ell_S]/\Delta t$ 个),所以触发点的剩余比例至少为这部分占 $n$ 的比值。论文配合给出真实控制频率示例(如 $30$ FPS $\to \Delta t=33,$ms),并分析了不同 $g$ 对队列曲线的影响(下图)。 数据 论文中提到的复现配置如下: 模型与输入:冻结 VLM,仅训动作专家;取 前半层 $N=\lfloor L/2\rfloor$ 的 $H^{(N)}$ → 投影成 $O_N$。图像 512×512;64 视觉 token/帧;状态→1 token;bfloat16。 动作块与解算: 每段 $n=50$;推理 10 步 Flow-Matching 积分。 优化:训练 200k step;global batch 256;AdamW($\beta_1=0.9,\ \beta_2=0.95$);余弦退火学习率 $1\times10^{-4}\to2.5\times10^{-6}$。 参数量: 总计 ≈450M;动作专家 ≈100M;若 VLM 有 32 层,取前 16 层。 论文中提到需要关注的信息: 模拟(LIBERO/Meta-World):中等规模(~0.45B)已对标/超过若干更大基线;放大到 ~2.25B 继续提升。 真实机器人(SO100/101):多任务平均成功率 ≈78%,优于 π0 与 ACT。 异步 vs 同步:成功率相近,但异步平均完成时间缩短 ~30%,固定窗口内完成次数显著更多。 论文中提到的落地经验: 形状与缓存:把 $H^{(N)}(T\times d_o)$ 投到 $d_a$ 后当 K/V;两次 Cross 复用 KV 缓存。 因果掩码:Self-Attn 必须用因果掩码(第 $i$ 步不可看未来)。 视觉压缩:优先用 space-to-depth 固定 64/帧;任务特别细腻时用 $r=2$(256 token)或多尺度/ROI 方案。 起步超参:$n=50$、积分步数 10、$N=\lfloor L/2\rfloor$、$d_a=0.75d$。 异步阈值:按 $g\ge\frac{\ell_S/\Delta t}{n}$ 设定,取略高于下界更稳;配合相似度过滤与重叠拼接。 动作归一化:对不同量纲(角/位移/速度)做标准化,训练更稳、积分不发散。 交替注意力有效:Cross + 因果 Self 明显优于单一注意力;“用前半层”普遍优于“直接换小 VLM”。 参考:https://arxiv.org/abs/2506.01844 -
浅析Pi0 :VLM 与 Flow Matching 的结合之道
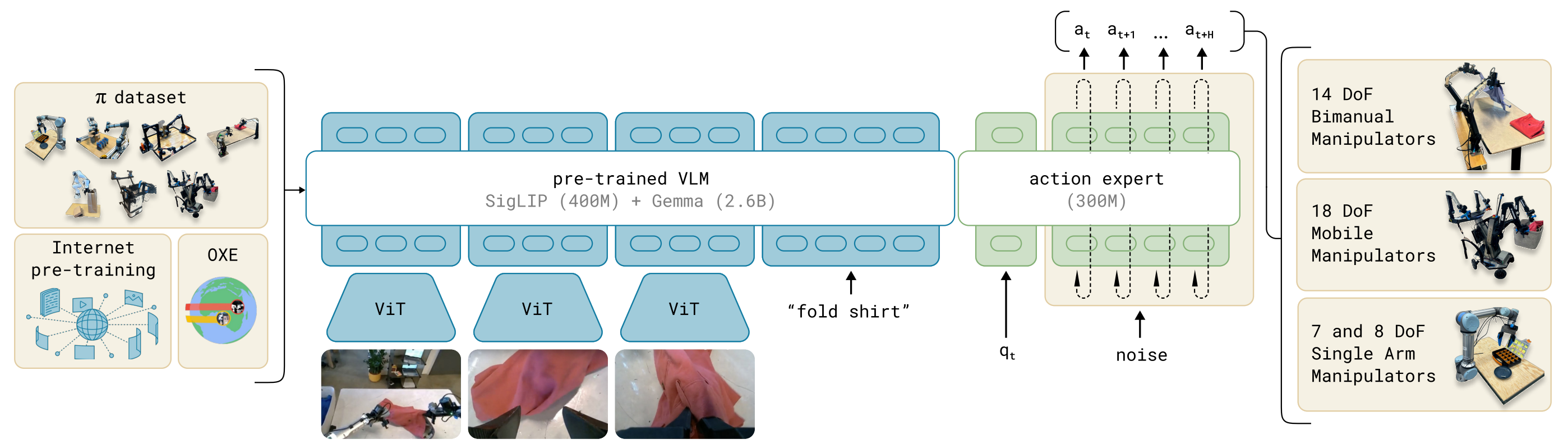
概述 传统机器人策略模型往往局限在单一任务或平台,难以跨场景泛化。与此同时,大规模 视觉-语言模型(VLM) 已展现出卓越的语义理解与任务指令解析能力。如果能将 VLM 的语义理解能力 与 Flow Matching 的连续动作建模能力 结合,有望构建具备泛化与实时性的机器人通用控制器。 Pi0 (π0)正是这样一个探索:基于 PaliGemma(3B 参数 VLM) 作为感知与语义主干,结合 Flow Matching 动作生成器,实现语言到多机器人动作的端到端建模。它借鉴了大语言模型的“预训练 + 微调”范式,把互联网级别的语义知识和机器人操控数据结合起来,从而实现跨平台、跨任务的通用机器人控制。 我们此前分析了VLM、Flow Matching原理,掌握这些之后理解Pi0是非常简单的。 原理 结构 模型结构主要有VLM主干+ Action Expert动作专家构成。 VLM主干:基于 PaliGemma(一个 3B 参数的 VLM),继承互联网规模的图像+语言知识。 Action Expert(动作专家):额外的子网络,负责用 Flow Matching 方法预测连续动作向量。 模型的输入包括观测的多视角RGB图像、语言指令、机器人自身状态(关节角、传感器),经过模型处理后输出为高频动作序列(每秒50HZ动作chunk),这些动作控制单臂、双臂、移动操作臂等多类机器人。 训练 我们训练的目标是让$A_t^0 \sim \mathcal{N}(0, I)$ ——>$A_t$(真实动作),希望模型学会如何把一个“噪声动作”流动成一个真实的动作。就像扩散模型是“噪声 → 图像”,这里是“噪声动作 → 专家动作”。 在训练的时候要让噪声动作流向真实动作,我们需要构建一个路径,这里依旧使用的是直线路径。 $$ A_t^\tau = \tau A_t + (1-\tau)\epsilon, \quad \epsilon \sim \mathcal{N}(0,I) $$ 这个公式跟我们在Flow Matching文章中的训练公式是不是一样的。我们在噪声动作$\epsilon$和真实动作$A_t$之间,采样一个"插值点"。$\tau $表示时间的进度,当$\tau = 0$时完全是噪声,当$\tau = 1$时完全是真实动作,这个就构造了一条噪声到动作的直线路径。 我们的目标是要让模型告诉我们"从当前点$A_t$应该往哪个方向移动,才能逐渐靠近真实动作",因此就是在计算在每个时间速度。 $$ u(A_t^\tau \mid A_t) \triangleq \frac{d}{d\tau} A_t^\tau $$ 代入公式可得: $$ \frac{d}{d\tau} A_t^\tau = A_t - \epsilon $$ 而论文中成$u(A_t^\tau \mid A_t) = \epsilon - A_t$,只是方向约定相反,本质上没有差异。上面的公式,目标速度就是噪声 - 动作,它定义了“流动的方向”。就像在地图上,目标向量场就是指路的“箭头”。这样得到了真实的速度场,我们就可以在训练的时候计算损失了。 $$ L(\theta) = \mathbb{E}\big[ | v_\theta(A_t^\tau, o_t) - u(A_t^\tau \mid A_t) |^2 \big] $$ $v_\theta$是神经网络(Action Expert),输入 当前 noisy action + 观察$o_t$,输出预测的速度场。损失函数就是 预测的速度场 vs 真实的目标速度场 的均方误差 (MSE)。训练目标:让模型学会在任意中间点给出正确的“流动方向”。 推理 $$ A_t^{\tau+\delta} = A_t^\tau + \delta v_\theta(A_t^\tau, o_t) $$ 推理生成也比较简单,从噪声动作$A_t$开始,每次迭代一步:输入当前的$A_t^\tau $和观察的$o_t$,接着模型给出速度场,就沿着这个方向走一步(步长$\delta$),然后按照这个步骤重复迭代,最终得到真实的动作$A_t$。和扩散模型不同:这里不需要几十/上百步,只要 ~10 步 ODE 积分,就能得到高质量动作,适合机器人实时控制。 参考: https://arxiv.org/abs/2410.24164 -
Flow Matching:让生成模型“流动”起来
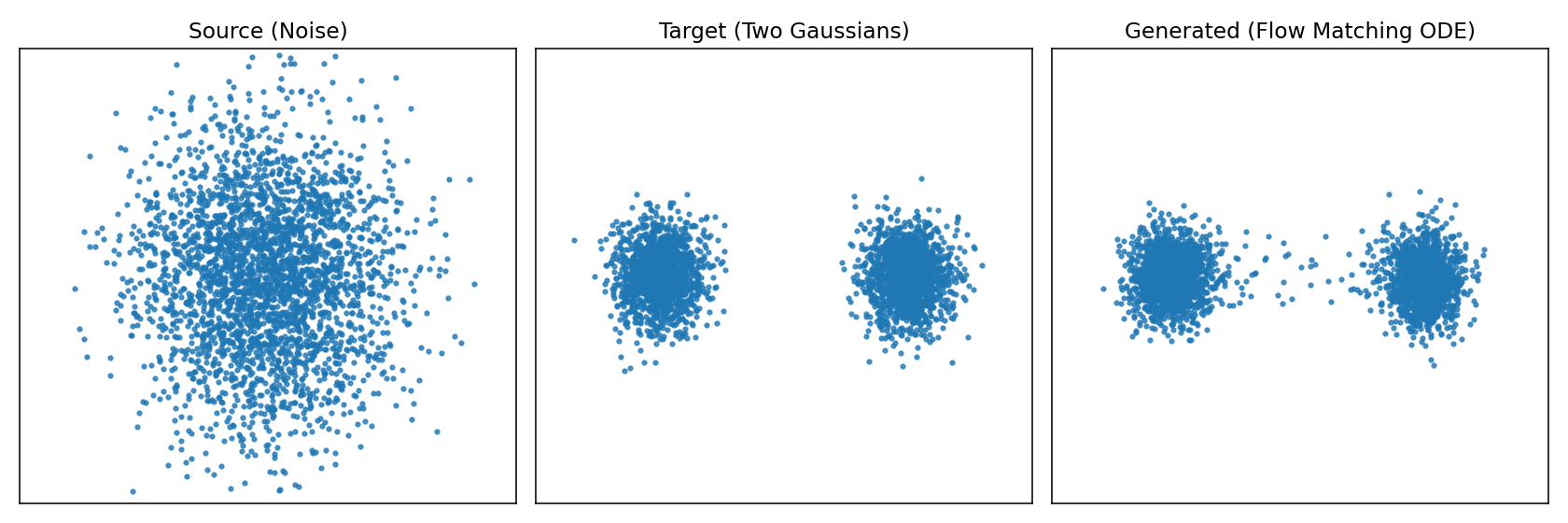
背景 上一篇文章分析了diffusion扩散模型。diffusion扩散模型做法是加噪声、再一步步去噪,训练过程复杂,还需要 carefully 设计噪声调度。 Flow Matching提出了更直接的方式:与其通过一大堆离散的“加噪/去噪”步骤,不如直接学习一个连续的流动 (flow),让点从噪声“顺滑地流动”到目标数据。 原理 把生成过程看作流体运动,想象有一堆水滴(噪声),通过一个力场,它们会被推动、流动,最后聚集成目标形状(真实分布的数据)。Flow Matching从物理学角度学一个"速度场",让数据点从"源分布(噪声)"流动到"目标分布(真实数据)"。 如图所示左边是源随机点云,中间是目标形状,右边是实际使用模型生成的形状。为了更直观的体会再来看下图从源分布逼近目标分布的过程。 左图就是源分布的点在不同时间应该朝那个方向运动直到最终的目标分布,右图是不同时刻让这些点应该往哪个方向进行流动速度场。 接下来看看数学怎么表示,我们希望从源分布$p_{src}$(比如高斯分布)按照流动的方式到目标分布$p_{data}$,那么方式就是在每个时间$t$为每个点$x$都指定一个速度$v_\theta(x,t)$,这样在不同时间就知道点该往哪里动,那么点的轨迹就完全确定了。在数学上点的位置$x(t)$随着时间变化,那就是速度场向量,即常微分方程 $$ \frac{dx}{dt} = v_\theta(x, t) $$ 左边的$\frac{dx}{dt}$描述的是随时间的变化率,右边$v_\theta(x, t)$就是我们要学习的"速度场",它给出"$t$时刻,位置$x$应该往哪里动"。 总结一下Flow Matching 里速度场写成 ODE,是因为它给出“点的位置随时间的变化率”,这正是常微分方程的定义,生成过程就是解 ODE,从噪声轨迹流到数据。 推理 模型要做的事情就是要预测出下一个时间刻应该往哪里走,输出是一个速度场;推理的过程就是解常微分方程ODE。 输入:当前位置$x \in \mathbb{R}^d$,当前时间$t \in [0,1]$。 输出:模型计算输出当前的速度向量,即$\frac{dx}{dt} = v_\theta(x,t)$。 更新:根据速度向量$v_\theta(x,t)$通过积分公式把所有时间段速度累积起来得到最终点$x(1)$。 $$ x(1) = x(0) + \int_{0}^{1} v_\theta(x(t),t)\,dt $$ 直观理解就是神经网络提供"切线方向",积分就是"把所有切线拼起来",形成完整的轨迹,从噪声走到目标分布。 但实际过程中我们用离散的数值方式,比如欧拉法,如下: 时间从$t$=$0$到$t$=$1$,分成若干小步(比如50或100步),在每一步按照上面公式更新。 输入:当前的位置$x_k$和当前时间步$t_k$。 输出: 模型预测计算速度向量场$v_\theta(x_k, t_k)$。 更新:通过欧拉法更新公式更新下一步位置$x_{k+1} = x_k + v_\theta(x_k, t_k)\Delta t$ 每一步模型计算出速度向量$v_\theta(x_k, t_k)$然后根据公式进行更新下一步的位置,新位置=旧位置+速度x时间步长;$v_\theta(x_k, t_k)\Delta t$计算每次迭代的移动距离(速度x时间),这就是基本的欧拉积分法,直观的意义是在短时间$\Delta t$内,点会沿着速度场方向前进一点。不断的进行多步迭代,从$x_0$出发,逐步得到$x_1$,$x_1$,$x_2$,$x_3$,....,$x_k$,当$k$=$K$时,$t_K$=$1$,就得到最终的$x(1)$。 怎么理解$t_k$、$x_k$、$\Delta t$? $t_k$是第$k$步对应的时间点,如果flow matching的时间区间是[0,1],我们把它切成$K$个小步(如50或100步),每个时间点就是$t0$=$0.00$,$t1$=$0.01$;$\Delta t$是时间步长如把时间区间[0,1]均匀分成100步,那么$\Delta t$=$1/100$=$0.01$;$x_k$是表示在$t_k$时的点(或点云),初始时从高斯噪音采样到。 下面再来一个直观图展示了Flow Matching推理的过程。 灰色箭头:代表速度场$v_\theta(x_k, t_k)$,告诉每个位置的点应该往哪里走。上图设定的目标是(2,2)。 绿色点:初始$x(0)$来自噪声分布即源分布。 红色叉:表示目标位置,代表数据分布的一个样本区域。 蓝色折现轨迹:数值积分结果,点一步一步验证速度场北推向目标。 训练 我们希望模型学会把源分布$p_{src}$流动到目标分布$p_{data}$;换句话说就是有$x_0 \sim p_{\text{src}}$,输出目标点$x_1 \sim p_{\text{data}}$我们要训练一个速度场网络$v_\theta(x_k, t_k)$,让它指导点$x_t$沿正确的路径从$x_0$——>$x_1$。 要训练行动轨迹需要知道真实轨迹这样才能和实际预测值做比较求损失,而训练的关键却正好是不知道真实的速度场。那如何构建训练的目标了?可以设计一个简单的"参考轨迹",如直线路径$x_0$——>$x_1$。 $$ x_t = (1 - t)x_0 + tx_1 $$ 给定输入样本$(x_0 \sim p_{\text{src}},x_1 \sim p_{\text{data}})$,其中$x_0$是源随机位置,$x_1$是目标位置。在训练的时候我们自己定义一条直线路径$x_0$——>$x_1$,我们不能一步到位,而是要有一个流动的过程。 这条直线路径上的真实速度公式对$t$求偏导,而恰巧速度是一个常数(始终指向目标点$x_1$)。 $$ u^\star = \frac{dx_t}{dt} = x_1 - x_0 $$ 既然速度方向就是一个常数$x1-x0$,为什么不直接一步把$x1$变成$x0$,而要搞成连续流动了? 如果一步到位公式就变成$x_1 = x_0 + (x_1 - x_0)$,相当于直接跳到目标点,完全不需要ODE、积分、网络。但问题在于训练时我们有配对的$(x_0, x_1)$,所以能写下$(x_1-x_0)$,而推理时了我们只有$x_0 \sim p_{\text{src}}$,并不知道该对应那个$x1$,因此不能一步到位,因为没有$x_1$可直接计算。 最后我们训练目标就是网络预测的速度$v_\theta(x_k, t_k)$,损失就网络预测的速度$v_\theta(x_k, t_k)$与真实的速度$x_1-x_0$的均方误差。训练完成之后,网络就学会了在任何位置$x_t$、时间$t$给出正确的速度场。 $$ \mathbb{E}\Big[ || v_\theta(x_t, t) - (x_1 - x_0) ||^2 \Big] $$ 源码示例 为了加深理解,程序实现一个最小的 Conditional Flow Matching(直线路径的 Rectified Flow)示例,学习时间条件速度场 vθ(x,t),把二维标准高斯源分布推到左右两个高斯簇的目标分布。训练后输出两张图:训练损失曲线 cfm_loss.png,以及三联静态图 cfm_overview.png(源/目标/生成)。 # -*- coding: utf-8 -*- # Flow Matching demo: source N(0,I) -> target: Two Gaussians (left & right) # 输出: # 1) cfm_loss.png(训练损失) # 2) cfm_overview.png(三联图:Source / Target / Generated) # 依赖:pip install torch matplotlib import time, warnings warnings.filterwarnings("ignore", category=UserWarning, module="matplotlib") import numpy as np import torch, torch.nn as nn, torch.optim as optim import matplotlib matplotlib.use("Agg") import matplotlib.pyplot as plt # ------------------------- 配置 ------------------------- device = torch.device("cuda" if torch.cuda.is_available() else "cpu") torch.manual_seed(0) XLIM = (-4.0, 4.0) YLIM = (-3.0, 3.0) # ------------------------- 数据分布 ------------------------- def sample_source(n): return torch.randn(n, 2, device=device) def sample_target(n): sigma = 0.35 means = torch.tensor([[-2.0, 0.0], [2.0, 0.0]], device=device) idx = torch.randint(0, 2, (n,), device=device) mu = means[idx] return mu + sigma * torch.randn(n, 2, device=device) # ------------------------- 模型:速度场 v_theta(x,t) ------------------------- class VelocityNet(nn.Module): def __init__(self, h=64): super().__init__() self.net = nn.Sequential( nn.Linear(3, h), nn.ReLU(), nn.Linear(h, h), nn.ReLU(), nn.Linear(h, 2), ) def forward(self, x, t): return self.net(torch.cat([x, t], -1)) # ------------------------- 训练(CFM,直线路径) ------------------------- def train_cfm(steps=2000, batch=512, lr=1e-3): net = VelocityNet().to(device) opt = optim.Adam(net.parameters(), lr=lr) loss_hist = [] t0 = time.time() for s in range(1, steps + 1): x0 = sample_source(batch) x1 = sample_target(batch) t = torch.rand(batch, 1, device=device) xt = (1 - t) * x0 + t * x1 u = x1 - x0 pred = net(xt, t) loss = ((pred - u)**2).mean() opt.zero_grad(set_to_none=True) loss.backward(); opt.step() loss_hist.append(float(loss)) if s % 200 == 0: print(f"[{s}/{steps}] loss={loss:.4f}") print(f"Train time: {time.time() - t0:.2f}s") return net, loss_hist # ------------------------- 采样(生成轨迹) ------------------------- @torch.no_grad() def generate_traj(net, n=3000, steps=60): x = sample_source(n) dt = 1.0 / steps traj = [x.cpu().numpy()] for k in range(steps): t = torch.full((n,1), (k + 0.5) * dt, device=device) x = x + net(x, t) * dt traj.append(x.cpu().numpy()) return traj # ------------------------- Matplotlib 工具 ------------------------- def save_loss(loss_hist, path): plt.figure(figsize=(6, 3.6)) plt.plot(loss_hist) plt.title("Training Loss (CFM)") plt.xlabel("step"); plt.ylabel("MSE") plt.tight_layout(); plt.savefig(path, dpi=140); plt.close() print(f"Saved {path}") def save_overview(src, tgt, gen, path): fig, axes = plt.subplots(1, 3, figsize=(12, 4)) titles = ["Source (Noise)", "Target (Two Gaussians)", "Generated (Flow Matching ODE)"] for ax, title, pts in zip(axes, titles, [src, tgt, gen]): ax.scatter(pts[:, 0], pts[:, 1], s=5, alpha=0.75) ax.set_title(title) ax.set_xlim(*XLIM); ax.set_ylim(*YLIM) ax.set_xticks([]); ax.set_yticks([]) plt.tight_layout(); plt.savefig(path, dpi=140); plt.close() print(f"Saved {path}") # (已移除 GIF 相关工具与依赖) # ------------------------- 主程序 ------------------------- if __name__ == "__main__": # 训练 net, loss_hist = train_cfm(steps=2000, batch=512, lr=1e-3) save_loss(loss_hist, "cfm_loss.png") # 数据与生成 src = sample_source(3000).cpu().numpy() tgt = sample_target(3000).cpu().numpy() traj = generate_traj(net, n=3000, steps=60) gen = traj[-1] # 三联静态图 save_overview(src, tgt, gen, "cfm_overview.png") # (已移除 GIF 生成步骤) print("All done.") (1)模型结构 模型结构为VelocityNet,使用了一个小型 MLP,输入 3 维(x 的 2 维 + t 的 1 维),输出 2 维速度向量。结构为Linear(3,64) → ReLU → Linear(64,64) → ReLU → Linear(64,2)。forward(x,t) 直接拼接 [x, t] 后送入网络。这里没有使用时间位置编码。 (2)训练过程 训练函数为train_cfm(steps=2000, batch=512, lr=1e-3),具体过程如下: 1) 每步采样源 x0 ~ source 和目标 x1 ~ target,独立均匀采样 t~U(0,1)。 2) 构造直线桥接点 xt = (1 - t)x0 + tx1。 3) 定义理想恒定速度 u = x1 - x0(常速,不依赖 t)。 4) 让网络在 (xt, t) 上预测 pred = vθ(xt,t),用 MSE(pred, u) 作为损失。 5) Adam 更新一次;每 200 步打印当前损失。 6) 返回训练好的 net 与 loss_hist。 直观理解,虽然 u 依赖 (x0, x1),但模型只观察 (xt,t)。训练学到的是条件期望 E[x1 - x0 | xt, t],也就是让网络在直线路径上学会把点往“正确方向”推的平均速度。这是直线路径 CFM 的核心思想。 (3)采样 采样函数为generate_traj,从源分布采样 n 个起点,设步长 dt=1/steps。用无梯度模式按欧拉法更新:对每步 k,用中点时间 t=(k+0.5)dt 预测速度 vθ(x,t),然后 x ← x + vθ(x,t)dt。记录每一步的点云到列表,返回整个轨迹(列表元素是 numpy 数组)。主程序中只使用最后一步作为“生成结果”。 (4)主流程 最后就是主流程先调 train_cfm 进行训练,保存 cfm_loss.png。分别采样 3000 个源样本 src 与目标样本 tgt。生成 n=3000、steps=60 的轨迹 traj,并取 gen = traj[-1] 作为最终生成样本。保存 cfm_overview.png,展示源/目标/生成的对比。 整体主要的实现点为 目标路径:x_t = (1 - t) x0 + t x1,直线连接源与目标。 理想速度:dx/dt = x1 - x0,使点沿直线以恒定速度匀速前进。 学习目标:在 (xt,t) 上回归 u = x1 - x0 的条件期望;推断时只需网络与当前状态,无需知道具体的 x0 或 x1。 数值积分:使用欧拉法简单高效;采用中点时间能略微减小离散误差。 -
Diffusion:如何从噪声中生成清晰图像
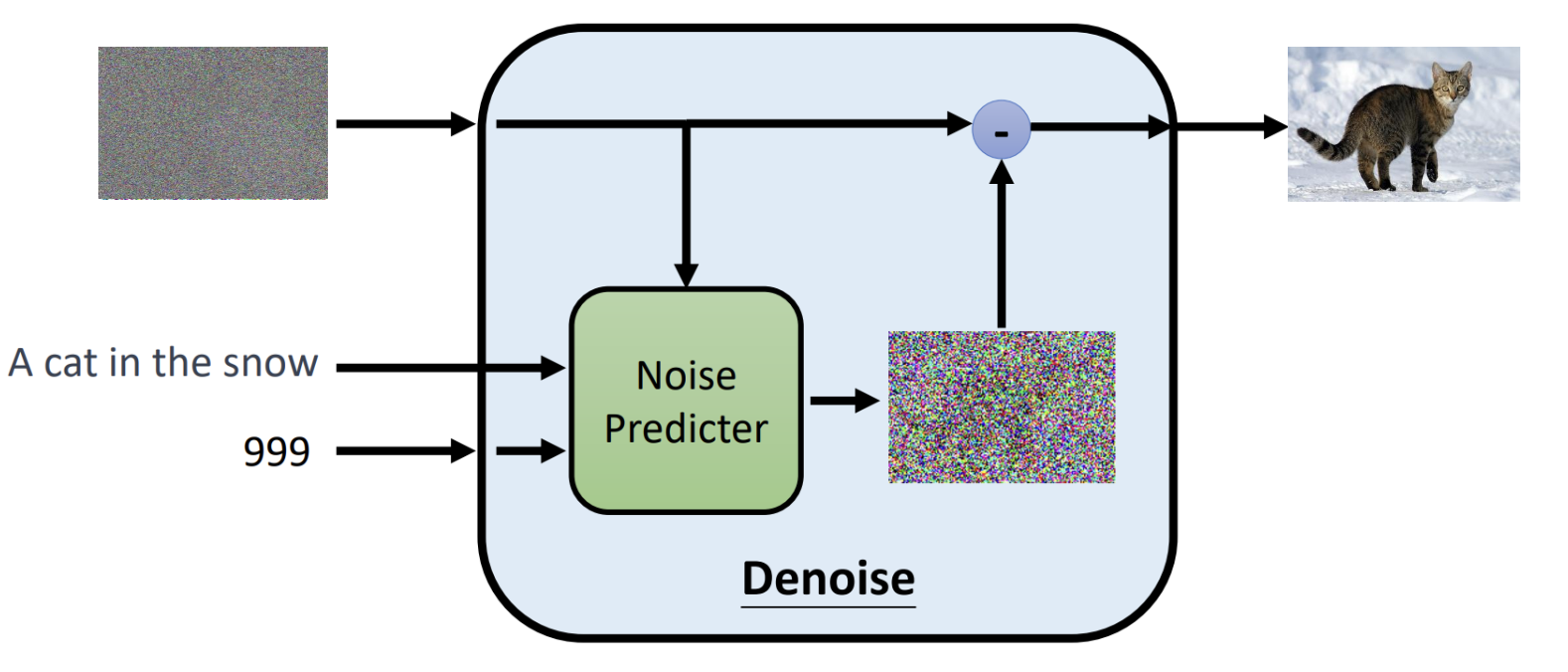
概述 图像生成是当下研究的热点,diffusion是一种人工智能领域图像生成的基础模型,当下Stable diffusion、DALL·E、MidJourney文生图模型的基座都使用了diffusion。 diffusion扩散模型属于生成式模型,生成图像不是正向从0到1构成图像而是反向的预先生成一个随机的噪声图中然后根据文本提示词逐渐的去噪"扣"出图像。主要思想是先训练一个权重模型,把一张清晰照片弄得越来越模糊(加入噪声),然后把模糊的图片融合文本提示词作为输入去训练一个模型学会“擦亮它”,反向恢复成清晰图像。训练完成后,就得到了模型的权重,那么使用这个权重模型只要给一副完全随机的“噪点图”和要生成图片的提示词,它就能一步步去掉噪声,变出一幅崭新、逼真的图片。 借用米开朗基罗雕刻"大卫像"时说的"我在大理石中看见天使,于是我不停地雕刻,直至使他自由”。而diffusion也是这样的原理,通过随机生成的一个噪声图片,结合输入的文字去掉噪音恢复到你想象的照片样子。 工作原理 推理 (1)输入阶段 输入阶段有3个输入信息,分别是随机噪声图像、文本提示、时间步。 随机噪声图像:最开始随机生成一个高斯噪声的图片。 文本提示:告诉模型,想要生成的内容是什么。 时间步:指明当前是去噪第几步,模型是一个多步迭代去噪的过程。按照数字依次递减进行迭代,数值越小去噪强度越弱。 (2)模型处理 核心组件是Noise Predictor(一般是一个U-Net结构神经网络),输入的带噪图像$X_{t}$、时间步$t$、以及提示文本通过Noise Predictor预测出这张图里有多少噪声,生成一张噪声图片$\epsilon^\theta(x_t, t, c)$。 (3)输出阶段 将输入-减去预测出的噪声图片就得到最后的去噪图片了,$x_{t-1} = x_t - \epsilon^\theta(x_t, t, c)$。 (4)迭代 迭代一轮得到一个降噪图片之后,接着将输出的降噪图片作为输入的带噪图片按照之前的步骤进行重复,直至$t$=$T$(比如$1000$)一直迭代到$t$=$0$得到最终的图像。当所有步骤完成后,随机噪声逐渐被“洗掉”,生成的就是一张符合条件描述的清晰图像。 下面是推理过程的算法伪代码 初始化:$x_T \sim \mathcal{N}(0, I)$从标准高斯分布中采样一个随机噪声向量(或噪声图像),作为生成过程的起点。 迭代循环:从$t$=$T$到$t$=$1$逐步迭代,每次去掉一部分噪声。如果$t$>$1$,额外采样一个噪声向量$z\sim \mathcal{N}(0, I)$。如果$t$=$1$,则$z$=$0$,即最后一步不加噪声。 核心公式:先去掉预测的噪声(括号里面的部分)得到更接近干净数据的样子,接着在进行缩放调整(除以$\sqrt{\alpha_t}$),最后加一点随机噪声$\sigma_t z$来保持生成的多样性。 输出:当循环结束时,最终的$x_0$就是最终生成的清晰图像了。 对于核心公式的参数这里稍微补充一下 参数 $\epsilon_\theta(x_t, t)$是预测的噪声; 参数$\alpha_t$取值范围是$0$~$1$,控制在第$t$步中保留多少原始图像信息加入多少噪声,当$\alpha_t$接近$1$时几乎保留全部信息,噪声小;当值趋于0时,原始信号衰减就大,噪声比例高; 参数$\bar{\alpha}_t$累积乘积参数,表示从第$1$步到$t$步累积保留原始信息的比例。 参数$\sigma_t z$随机扰动项,保持采样的多样性。 训练 训练模型我们需要把模型的输出结果和真实值进行比较才能进行梯度下降找到网络权重,那该如何设计准备训练结果和真实值的数据? diffusion模型的核心是要预测出图片的噪声分布然后减去预测的噪声得到真实的输出照片。以上图第一步进行说明,使用原始的图片,通过随机生成一个噪声图($x_{1}$)迭加作用到原始图片上这样就得到了模型的带噪声的输入图像,然后融合文本、时间步模型前向计算得到噪声图($x_2$)。已经知道了真实的噪声图是$x_{1}$,那么计算$x_{1}$和$x_{2}$的相似性就可以计算出损失了。 训练过程中关于图片-文本可以从Lion平台上获取,通过上面步骤取样照片然后不断加强噪声得到越来越模糊的图片送入模型预测进行计算迭代权重,让模型学会真正准确预测每一步中"加进去的噪声",训练完成之后,模型学会了如何"识别噪声",在推理时就从纯随机噪声$x_T$出发,通过文本提示词反向迭代去噪得到最终的想要的照片。 论文中的伪代码如下: repeat:表示循环执行训练过程。 采样数据:$x_0 \sim q(x_0)$从真实数据分布$q(x_0)$中采样一个训练样本比如一张猫。 随机采样时间步:$t \sim \text{Uniform}({1, \dots, T})$随机挑选一个扩散的时间步$t$,确保模型能在不同噪声水平都学会去噪。 采样噪声:$\epsilon \sim \mathcal{N}(0, I)$从标准的高斯分布中采样一份噪声,用于后续得到到原始图片上。 梯度下降更新参数:计算预测噪声和真实噪声$\epsilon$的均方误差。 模型 本章节简要说一下业界文生图模型,其结构可以总结为以上3个部分,文本编码器、生成式模型、解码器。 文本编码器:将用户输入的文本提示通过预训练的文本编码器如CLIP Text Encoder将自然语言转化为向量表示。 生成式模型:将编码的文本向量和噪声图像noisy latent作为输入,然后逐步迭代去噪。这里的模型如有diffusion、autoregressive等。输出是压缩到更低维的"潜在空间"。 解码器:将生成式模型的输入Latten Representation通过解码器还原最终生成清晰图像。生成式模型一般输出的是压缩的低维潜在空间,这样可以降低每一步迭代的计算量,最终加一个解码器来将其还原。 下面是stable diffusion、DALL-E、Imagen的模型结构图,核心组成都是上面3个部分,这里就不过多阐述了。 stable diffusion DALL-E Imagen 本文主要来自李宏毅Diffusion Model原理解析的笔记。