端侧 AI 与机器人技术雷达｜2026-07-31
今日必看 VisionPsy-Nano 把小型 VLM 的竞争压到视觉 token 预算 Tether AI Research 在 2026 年 7 月 29 日发布 VisionPsy-Nano 系列：VisionPsy-Nano-460M 主打质量，VisionPsy-Nano-460M-Flash 主打延迟，二
行业动态
文章列表
网站github page同步
准备 下载同步的仓库 mkdir blog git clone git@github.com:laumy0929/wordpress-export-to-markdown.git git clone git@github.com:laumy0929/notes.git git clone …
LeRobot SmolVLA：从训练到推理链路剖析
框架 本文主要对lerobot SmolVLA策略代码进行分析，下面是策略实现关键部分框图。 SmolVLAPolicay类封装向上提供策略的调用。SmolVLAConfig是对Smol
从数学角度理解flow matching中的线性插值
什么是插值 插值的核心问题是：在已知两个点的情况下，如何找到它们之间的中间点。 举个人走路的例子，起点在家门口(A点)，终点在公司(B点)，总的路程为1000米，假设人是匀速移动，如果
轻量SmolVLA：半层VLM、视觉压缩与异步推理赋能具身智能
概述 SmolVLA 是一套轻量级视觉-语言-行动（VLA）策略：前端用小型 VLM（视觉 SigLIP + 语言 SmolLM2）做感知与理解；后端用一个“动作专家”专门预测一段连续的低层控制。它与Pi0相比，参数
浅析Pi0 ：VLM 与 Flow Matching 的结合之道
概述 传统机器人策略模型往往局限在单一任务或平台，难以跨场景泛化。与此同时，大规模 视觉-语言模型（VLM） 已展现出卓越的语义理解与任务指令解析能力。如果能将 VLM 的语义理解能力 与 Flow Matching 的连
Flow Matching：让生成模型“流动”起来
背景 上一篇文章分析了diffusion扩散模型。diffusion扩散模型做法是加噪声、再一步步去噪，训练过程复杂，还需要 carefully 设计噪声调度。 Flow Matching提出了更直接的方式：与其
Diffusion：如何从噪声中生成清晰图像
概述 图像生成是当下研究的热点，diffusion是一种人工智能领域图像生成的基础模型，当下Stable diffusion、DALL·E、MidJourney文生图模型的基座都使用了
视觉 Token 如何注入语言模型？VLM拆解
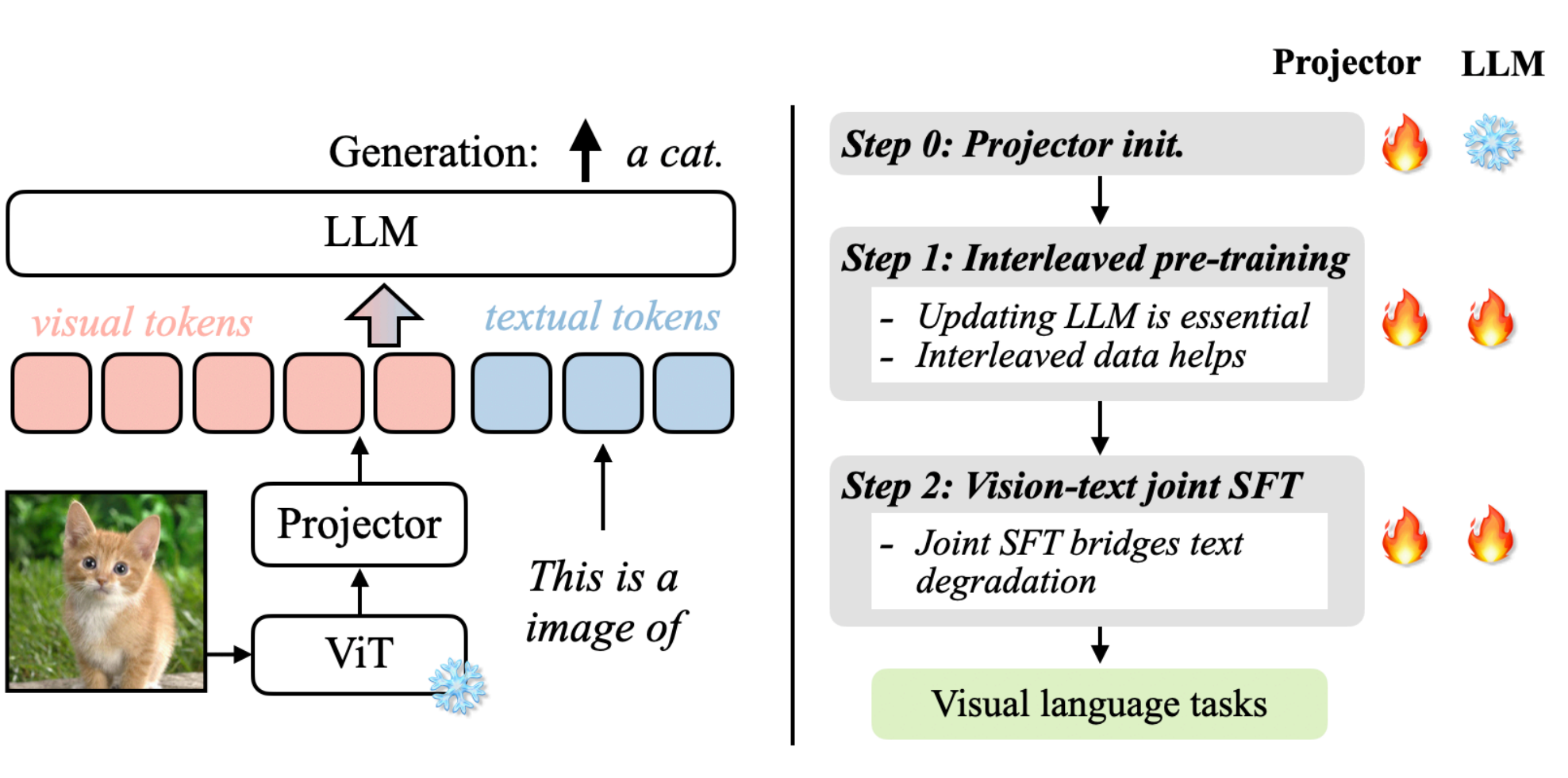
VLM与LLM 如果说我们有一张图片、一个图表想让大模型来帮忙理解那应该要怎么实现了？ 标准的LLM语言大模型只能处理文本序列，是不能够读取图像的，如果没有办法将视觉的数据转换为LLM
解读ViT：Transformer 在视觉领域如何落地
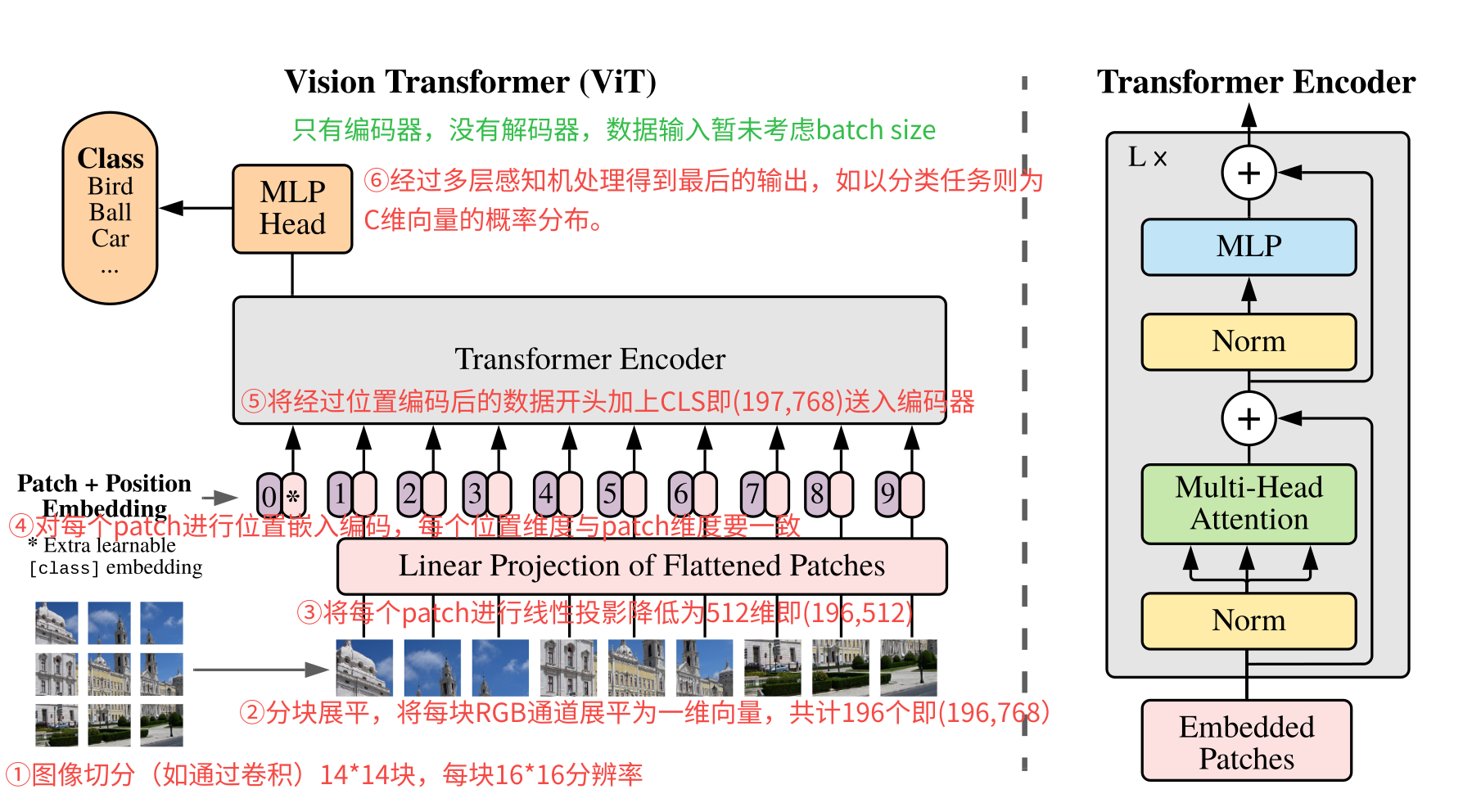
背景 计算机视觉领域，一直都是卷积天下。传统的卷积神经网络(CNN)依赖于卷积核提取局部特征，效果很好，但是也有一些不足，如需要人工设计卷积结构包括卷积核大小和层数，另外就是难以捕捉
lerobot之smolvla体验
环境安装 pip install -e ".[smolvla]" 在原来lerobot的环境基础上。 启动训练 本文主要是记录复现lerobot smolvla策略的效果，为了快速看到效果，这里不进行采集数据了，直接用此前ACT采集的数