最新文章
-

云服务器搭建YOLOv5训练环境
介绍 本文使用AutoDL云服务搭建YOLOv5的运行环境。 获取云服务器 在这个链接上https://www.autodl.com/home订阅服务,这里选择的是按量计费。 镜像选择基础镜像Mniconda最新ubuntu环境。 交钱订阅完成后就可以获取到登录的信息了。 这里使用的是ssh工具根据获取到的登录名和密码进行登录,需要注意的是端口可能不是默认的22,按照实际的端口进行。 配置conda环境 由于autoDL的服务器可能并不能访问外网,这里先将conda的源更换为清华的源。 conda config --remove-key channels conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/ conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/main/ conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/cloud/pytorch/ conda config --set show_channel_urls yes pip config set global.index-url https://pypi.tuna.tsinghua.edu.cn/simple 接下来创建和激活虚拟环境 conda create -n yolov5 python==3.8.5 # 创建虚拟环境名称为yolov5, python版本为3.8.5 conda activate yolov5 # 激活yolov5环境 conda init # 如果提示没有初始化conda环境的话,执行conda init后退出控制台重新登录,再次激活。 conda env list # 通过上面的命令可以查看当前创建的conda虚拟环境 拉取YOLOv5代码环境 通过官网链接获取YOLOv5的代码。 cd autodl-tmp/ #这里先切换到audodl-tmp目录,这个空间比较大,读写也比较快。 git clone https://github.com/ultralytics/yolov5 # 在github上拉取代码 如果要在本地使用vscode查看代码的话,可以参考:https://www.autodl.com/docs/vscode/ 这里需要注意的是,audoDL可能没有访问GitHub,处理的办法就是参考这个方法在服务器上面做一个代理,https://github.com/VocabVictor/clash-for-AutoDL 或者https://gitee.com/laumy0929/clash-for-AutoDL 获取到CLASH_URL如下示例: 截屏2025-07-17 12.34.36 截屏2025-07-17 12.39.15 按照yolov5的代码环境需要的包 pip install -r requirements.txt 安装完成后,进行推理测试,看看环境是否安装正常,执行detect.py 指定模型文件和输入图片进行测试。 python detect.py --weights yolov5s.pt --source data/images/bus.jpg 执行上面脚本是,会自动拉取预训练的模型yolov5s.pt,最终将推理结果存储到runs/detect/exp2目录下。 训练自定义数据集 这里从GitHub上抓了一个口罩的书籍集,https://github.com/iAmEthanMai/mask-detection-dataset.git,使用git clone拉取到本地。 git clone https://github.com/iAmEthanMai/mask-detection-dataset.git 查看mask的数据集配置,有3个分类。这里使用yolov5s进行微调,复制一份yolov5的模型配置文件,并修改分类为3,需要根据实际的数据集存放的位置调整一下路径。 cp models/yolov5s.yaml models/mask_yolov5s.yaml 配置完成后就可以进行训练了。 python train.py --data mask-detection-dataset/data/data.yaml --cfg models/mask_yolov5s.yaml --weights pretrained/yolov5s.pt --epoch 100 --batch-size 4 模型文件将输出到:runs/train/exp5/weights/ python detect.py --weights runs/train/exp5/weights/best.pt --source mask-detection-dataset/data/images/maksssksksss1.png 上面执行命令使用训练的模型文件测试看看效果。 -

YOLOv2和YOLOv3
YOLOv2 回顾一下YOLOv1有哪些缺陷? 边界框训练时回归不稳定,导致定位误差大。 每个网格只能预测两个边界框且只能识别一类目标。 小目标检测效果差。 针对以上的问题,YOLOv2进行了改进,下面从检测机制优化、网络结构优化、训练策略优化3个维度进行。 检测机制优化 锚框(Anchor Box)机制 YOLOv1每个网格只会预测一个目标,因为每个网格预测的B个边界框的类别概率都是共享的,要是有多2个目标的中心都落在了一个网格中,那么有一个目标就没法预测了。怎么解决了? 让每个边界框都对应一个类别概率,这样就能做到每个网格可以预测多个目标了。 每个边界框训练是没有基准的,这样训练的时候就很不稳定。如果预先定义边界框,使训练的时候按照这些预定义的边界框作为基准进行训练调整。这里做个类比来理解,假设我们的目标坐标是(8,8),那么如果没有设置基准,从坐标(0,0)找到(8,8)就相对比较远,那假设我们从(6,6)这个基准开始找,那找到(8,8)的概率就大了。 上面预先定义的边界框就称为先验框(anchor Box),那么新的问题来了,这个anchor Box我们每个网格设置多少个?设置什么样的形状了?实际的数据集中Ground Truth(真实标签)边界框有些是长方形、有些是正方形。 YOLOv2使用了K均值聚类算法用于生成先验框(Anchor Boxes),其核心目标是从训练数据中自动学习边界框的尺寸和比例,替代人工预设的锚框,从而提升检测召回率与定位精度。YOLOv2通过聚类COCO数据集,得到5个先验框尺寸(如(0.25,0.33), (0.5,0.75)...),覆盖常见物体形状。 pw,ph是先验框anchor的宽高(根据K类均值聚类得来),tx,ty,tw,th模型预测的偏移量(训练得到)。所以通过pw,ph,tx,ty,tw,th就可以计算出实际要预测的框bx,by,bw,bh。模型最终预测出tx,ty,tw,th这四个值就可以计算出bx,by,bw,bh。 这里需要注意 YOLOv2中对tx,ty进行了sigmod归一化,防止训练初期,中心点数值极大训练不稳定。 YOLOv2预测边界框的宽和高初始值是基于先验框而来,是模型对每个锚框输出宽高缩放因子(t_w, t_h),通过聚类生成的先验框指数变换得到最终宽高。而YOLOv1是根据图像实际宽高缩放而来。 全卷积网络与先验框 YOLOv1最后阶段使用的是全连接层,使用全连接层不仅仅参数量大,同时会将先前的特征图包含的空间信息破坏,在YOLOv2中改成了全卷积结构。 可以看到输出也发生了变化YOLOv1的输出是7 x 7 x (1+4+1+4+20),而YOLOv2输出是13 x 13 x k x (1 + 4 + 20),这里的k是每个网格的先验框数量,一般为5。(1+4+20)分别是锚框的置信度、边界框坐标、类别概率,每个anchor先验框都对应一个(1+4+20),也就是说每个先验框可以检测一个目标,这样就解决了YOLOv1中每个网格只能检测一个目标的问题,YOLOv2中每个网格有5个先验框,就可以检测最多5个类别。 网络结构优化 加入批量归一化: YOLOv1中每层卷积都是由线性卷积+非线性激活函数组成,由于批量归一化得到越来越普遍的应用,并且效果较好,因此在YOLOv2每层卷积层都加入了批量归一化。所以卷积层就变成了线性卷积+归一化+非线性激活函数组成。 融合高分辨率特征图:YOLOv1输出的特征图是13 x 13 x 1024,分辨率越低丢失的特征就越多。为了解决这个问题,YOLOv2在第17层单独抽出一层26 x 26 x 512的特征图,然后通过特殊的降采样得到13 x 13 x 256的特征图,最后将这个13 x 13 x 256的特征图与前面13 x 13 x 1024的相加,这样达到提高特征信息保留。 多尺度训练 YOLOv2在训练上也做了进一步的优化,因为同一张图像,缩放到不同尺寸,不同尺寸包含的图像信息也不同。因此为了提高精度,引入了多尺度训练训练机制。 具体就是在训练网络时,对图像按照320、352、384、416、448、480、512、544、576、608等不同输入尺寸进行训练。 总结一下,YOLOv2针对YOLOv1的改进点有以下。 增加先验框机制:每个网格使用K类均值聚类预设K个先验框作为基准训练。每个先验框负责预测一个目标。 加入批量归一化:每个卷积层对训练数据做批量归一化处理。 高分辨率特征图:网格划分13 x 13,主干网络中抽离一路高分辨率特征图进行特殊处理然后再加回去。 对尺度训练:训练阶段使用不同尺度的图像数据进行训练。 YOLOv3 对应目标检测网络可以由主干网络、颈部网络、检测头。 主干网络:提取多尺度特征。通过卷积层、池化层等操作,将输入图像逐层抽象化,生成不同层级的特征图。有浅层特征和深层特征。浅层特征是保留细节(如边缘、纹理),适合小目标检测;深层特征是蕴含语义信息(如物体整体结构),适合大目标识别。 颈部网络:融合与优化特征。连接主干网络与检测头,整合不同层级的特征图,增强模型对不同尺度目标的感知能力。 检测头:执行具体检测任务。基于融合后的特征,输出目标的位置、类别及置信度。 YOLOv2对于小目标的检测还是不够精确,这一缺陷的主要原因是YOLOv2只使用了32倍的降采样率。 浅层卷积层:没有经过更多的卷积层处理,提出的语义信息较少,具有较浅的语义信息;但对应没有过多的降采样因此具备较多的位置信息。 深层卷积层:经过更多的卷积层处理,提取更多的语义信息;但是位置信息经过了太多的降采样,丢失了位置信息。 语义信息可以理解为是什么类别的物品,位置信息是这个物品在图中的什么坐标位置。浅层卷积层更适合检测小目标(语义信息不需要这么多),深层卷积层适合检测大目标(需要更多的语义信息)。根据这个认知,YOLOv3主干网络就使用了3个不同尺寸的特征图,分布对应的降采样是32、16、8倍。对于小尺度目标使用的是8倍将采样并在浅层网络进行先提出输出针对性处理。而大尺度目标使用32倍降采样在最深层的网络中进行输出。 输入是416 x 416的图像,输出的是3个特征图,分布是C1=B X 256 X 52 X 52;C2=B x 512 x 26 x 26;C3=B x 1024 x 13 x 13,这里的B是先验框,一般为3。针对输入图像做了52x52、26x26、13x13三种不同疏密度的网格。 3个特征图根据多级检测结构推理后,得到最终预测的3个结果。y1= B x (4 + 1 + Nc) x 13 x 13;y2= B x (4 + 1 + Nc) x26 x 26;y3= B x (4 + 1 + Nc) x 52 x 52; 其中B为先验框数量,一般是3。Nc是类别个数,根据实际数据集,YOLOv3使用的是COCO数据集,有80个类别。 参考: 书籍《YOLO目标检测》 -

YOLOv1目标检测原理
介绍 YOLO在目标视觉检测应用广泛,You Only Look Once的简称。作者期望YOLO能像人一样只需要看一眼就能够立即识别其中的物体、位置及交互关系。能够达到快速、实时检测的效果。 YOLO检测系统可以简要分为3个步骤: Resize image:调整输入图像的大小为448 x 448。 Run Convolutional network:CNN卷积网络处理。 Non-max suppression:使用非极大值抑制。 YOLO与其他目标检测系统有什么不同或优势? YOLO 非常简单,如上图。单个卷积网络可以同时预测多个边界框及其类别概率。YOLO 使用完整图像进行训练,并直接优化检测性能。与传统的目标检测方法相比,这种统一的模型具有诸多优势。 首先,YOLO速度极快。由于YOLO将检测视为一个回归问题,因此无需复杂的流程。只需在测试时对一张新图像运行神经网络即可预测检测结果。 其次,YOLO在进行预测时会全局推理图像。与滑动窗口和基于区域提议的技术不同,YOLO在训练和测试期间会查看整幅图像,因此它隐式地编码了关于类别及其外观的上下文信息。Fast R-CNN 是一种领先的检测方法,由于无法看到更大的背景,它会将图像中的背景块误认为是物体。与 Fast R-CNN相比,YOLO 的背景错误率不到一半。 最后,YOLO学习的是可泛化的对象表征。在使用自然图像进行训练并在艺术作品上进行测试时,YOLO 的表现远超DPM和R-CNN 等领先的检测方法。由于 YOLO 具有高度的泛化能力,因此在应用于新领域或意外输入时,它不太可能崩溃。 更为详细的结构如下: 该网络包含24个卷积层和2个全连接层。不同于GoogLeNet使用的Inception模块,我们采用1×1降维层接3×3卷积层的简单设计。输入是448 x 448 x 3张量,最终输出是7×7×30的预测张量。 检测原理 YOLO是做统一检测,其网络使用整幅图像的特征来预测每个边界框。它还能同时预测图像所有类别的所有边界框。这意味着YOLO网络对整幅图像及其中的所有物体进行全局推理。 划分网格: 将输入图像划分为S X S个网格(grid)。 预测边界框:每个网格预测B个边界框(包含4个预测值x、y、w、h)并计算这些边界框的置信度分数以及C个条件类别概率。 置信度分数计算方式为:当网格中不存在任何物体,则为0,如果存在则等于预测框与真实框的交并比IOU。 C个条件类别概率:是C个预测类别,每个类别的概率值。因此总结一下,预测值为S X S X (B X 5 + C)个tensor。这里要注意的是,边界框的中心点并不是网格中心点,但中心点落在的这个网格负责这B个边界框的预测。 上面的图出之YOLOv1论文中的第5版本,如果不是很直观可以看看第1个版本,只不过第一个版本每个网格只预测一个边界框并且没有包含置信度。 为什么YOLOv1改进加了一个置信度? 预测框与真实框的交并比(定位质量),这样可以预测质量。YOLO将图像划分为网格,每个网格仅预测一组类别概率(与预测框数量无关),若直接用类别概率判断物体存在性,会忽略定位质量。例如一个网格预测出“狗”的概率为90%,但预测框可能严重偏离真实物体(IoU低),此时置信度会因低IoU而降低,避免高类别概率但定位差的误检。 为什么YOLOv1最开始每个网格是一个边界框后面变成了多个? 单框局限:每个网格仅预测一个边界框时,模型难以适应不同长宽比的物体(如瘦高的行人和扁平的汽车)。 多框设计:通过预测两个不同长宽比的边界框(如一个方形、一个长方形),模型可灵活匹配不同形状的目标,提高定位精度。 训练机制:训练时,选择与真实框IoU更高的预测框负责该物体,另一个框则被抑制(不参与损失计算),从而驱动网络学习多样化的边界框表达。 单框瓶颈:网格内若存在多个重叠目标(如密集人群),单框设计只能检测其中一个物体,导致漏检49。 冗余预测:两个边界框提供双重检测机会,即使一个框被错误抑制,另一框仍可能捕获未被覆盖的目标811。 但是这里需要注意的是,在YOLOv1中,同一个网格内的两个边界框(边界框1和边界框2)预测的类别结果是同一个类,因为类别的预测是共享的,也就是说预测的类别概率是共享的,每个网格只能预测一个类别目标。这也是YOLOv1的缺陷,如果有2个不同类别的物体中心都落在了同一个网格中,这样就没有同时预测两个物体。 总结:YOLO系统将检测建模为回归问题,它将图像划分为 S × S 的网格,并为每个网格单元预测 B 个边界框、这些框的置信度以及 C 个类别概率。这些预测被编码为S × S × (B ∗ 5 + C) 张量。为了在 PASCAL VOC 上评估 YOLO,作者使用 S = 7,B = 2。PASCAL VOC 有 20 个标记类别,因此 C = 20,最终预测是一个结果是7 × 7 × 30的张量。 损失函数 YOLOv1的损失函数使用的是边界框坐标(x,y,w,h)、置信度、类别概率计算而来,公式如下图。 边界框坐标损失:第一第二行公式,计算的是边界框坐标的损失。 置信度损失:分为有目标和无目标,无目标学习标签就是0,有目标学习标签是1. 类别损失:每个类别的损失,针对的是每个网格单元的损失,不是预测框的。 关于边界框的位置参数是怎么样的?下面总结一下: tx, ty: 是边界框中心坐标相对于当前网格(第5行第二列)左上角的偏移量(归一化到 [0,1] 区间)。 w, h: 是边界框的实际宽度和高度归一化到 [0,1],相对于整张图像的尺寸宽和高进行进行缩小比例。 详细的计算公式: 中心点坐标:x = (C_x + tx) / S, y = (C_y + ty) / S,(C_x, C_y为网格左上角坐标,S为网格划分数量) 宽高:w = 框宽 / 图宽, h = 框高 / 图高 YOLOv1的边界框参数优点是直接预测实际位置,无需先验框(Anchor Box),模型结构简单。缺点就宽高直接回归导致训练不稳定,定位精度较低; 模型后处理 YOLOv1模型训练完成后,给定一个448 x 448 x 3的tensor,模型输出是一个7 x 7 x 30的 tensor,也就是每个网格位置包含2个边界框的置信度输出C1和C2,两个边界框的位置参数(tx1,ty1,w1,h1)和(tx2,ty2,w2,h2)以及20个类别的概率p1~p20。 显然上面的输出结果不是我们想要的,我们要进行处理,筛选出最优的值,具体的处理步骤如下: 计算所有边界框得分:每个网格预测的边界框进行计算得分,计算公式分数=置信度值 x 类别概率中最大的值。 阈值剔除: 根据上一个步骤计算的得分,设定一个阈值比如0.3, 剔除小于阈值分数的边界框。 计算边界框位置:剔除一部分阈值后,计算编辑框的参数位置包括x,y,w,h。 非极大值抑制:经过前面的步骤后,同一个目标可能还是有多个预测边界框,最后试用非极大值抑制将重复检查的框去掉。最后就得到下面的示例结果。 总结一下YOLOv1的优缺点: 优点: 速度快,实时性强:首次实现端到端训练,推理速度达 45 FPS,简化了检测流程。 结构简单: 统一为单一回归问题,避免了区域提议(Region Proposal)的复杂步骤。 计算效率高:全卷积网络设计,适合资源受限的嵌入式设备。 缺点: 检测精度低:每个网格仅预测2个边界框且只能识别单一物体,同时对密集小目标检测效果差网络划分7x7精度不够。 定位不准确:边界框回归不稳定,导致定位误差大,与边界框的宽高定义为实际宽高缩放有关。 灵活性差:输入分辨率固定(448×448),不支持多尺度训练,网格划分(如 7×7)限制检测数量上限(最多 49 个物体)。 泛化能力弱:对非常规长宽比或重叠物体处理效果差。 参考: 1. 论文:https://arxiv.org/pdf/1506.02640v5 2. 书籍《YOLO目标检测》 -

opencv视频流
环境准备 本文通过采集USB摄像头来示例说明 export LD_LIBRARY_PATH=/mnt/extsd/usr/lib:$LD_LIBRARY_PATH #指定库的路径 cat /sys/devices/platform/soc/usbc0/usb_host #激活USB host 摄像头采集 摄像头相关的主要使用的是VideoCapture类。 打开摄像头 cv::VideoCapture cap; // 创建视频捕获对象 cap.open(0); // 打开默认摄像头(通常为/dev/video0) if (!cap.isOpened()) { std::cerr << "无法打开视频设备" << std::endl; return -1; } 设置参数 cap.set(cv::CAP_PROP_FRAME_WIDTH, 640); // 设置宽度 cap.set(cv::CAP_PROP_FRAME_HEIGHT, 480); // 设置高度 cap.set(cv::CAP_PROP_FPS, 30); // 设置帧率 采集数据 cv::Mat frame; while (true) { cap >> frame; // 捕获一帧 if (frame.empty()) { std::cerr << "捕获帧失败" << std::endl; continue; } // 在此处理帧数据... usleep(1000000 / frame_rate); // 30ms延迟,控制帧率 } 推流显示 主要是打开/dev/fb0,然后写入数据。 获取显示参数 通过ioctl的方式,获取显示分辨率,像素位深(每个像素的占用内存大小),以便将采集到的摄像头数据调整为合适的尺寸进行显示。 struct framebuffer_info get_framebuffer_info(const char* framebuffer_device_path) { struct framebuffer_info info; struct fb_var_screeninfo screen_info; int fd = -1; fd = open(framebuffer_device_path, O_RDWR); if (fd >= 0) { if (!ioctl(fd, FBIOGET_VSCREENINFO, &screen_info)) { info.xres_virtual = screen_info.xres_virtual; //虚拟水平的分辨率,包含不可见区域,即虚拟宽度 info.bits_per_pixel = screen_info.bits_per_pixel; //每个像素的位深,即像素大小,如16/24/32等 info.xres = screen_info.xres; //实际水平分辨率,即实际宽度 info.yres = screen_info.yres; //垂直分辨率,即实际高度 } } return info; }; 尺寸调整 cv::resize(frame, frame, cv::Size(fb_info.xres, fb_info.yres)); 从/dev/fb0获取的实际分辨率进行调整尺寸。 格式转换 写入前,先将采集的视频帧转换为屏幕显示支持的格式,如RGB565,RGBA等。 switch (framebuffer_depth) { case 16: //转换为RGB565格式输出 cv::cvtColor(frame, framebuffer_compat, cv::COLOR_BGR2BGR565); break; case 32: //转换为RGBA格式输出,添加一个alpha通道 std::vector<cv::Mat> split_bgr; cv::split(frame, split_bgr);//将BGR分离为3个通道,存储到split_bgr中。 split_bgr.push_back(cv::Mat(frame_size, CV_8UC1, cv::Scalar(255))); //创建一个全白的alpha通道矩阵并进行添加到一个新的通道 cv::merge(split_bgr, framebuffer_compat); //使用merge将3个颜色通道和alpha通道进行合并为RGBA四通道。 break; } 写入显示 ofs.seekp(0); //先进行定位 ofs.write(reinterpret_cast<char*>(framebuffer_compat.ptr(0)), framebuffer_compat.total() * framebuffer_compat.elemSize()); 也可以一行一行的写 for (int y = 0; y < frame_size.height; y++) { ofs.seekp(y * framebuffer_width * 2); ofs.write(reinterpret_cast<char*>(framebuffer_compat.ptr(y)), frame_size.width * 2); } 示例程序 #include <fcntl.h> #include <fstream> #include <iostream> #include <linux/fb.h> #include <signal.h> #include <stdint.h> #include <sys/ioctl.h> #include <unistd.h> #include <opencv2/opencv.hpp> static cv::VideoCapture cap; struct framebuffer_info { uint32_t bits_per_pixel; uint32_t xres_virtual; uint32_t xres; uint32_t yres; }; struct framebuffer_info get_framebuffer_info(const char* framebuffer_device_path) { struct framebuffer_info info; struct fb_var_screeninfo screen_info; int fd = -1; fd = open(framebuffer_device_path, O_RDWR); if (fd >= 0) { if (!ioctl(fd, FBIOGET_VSCREENINFO, &screen_info)) { info.xres_virtual = screen_info.xres_virtual; info.bits_per_pixel = screen_info.bits_per_pixel; info.xres = screen_info.xres; info.yres = screen_info.yres; } } return info; }; /* Signal handler */ static void terminate(int sig_no) { printf("Got signal %d, exiting ...\n", sig_no); cap.release(); exit(1); } int main(int, char**) { const int frame_width = 720; const int frame_height = 1280; const int frame_rate = 30; framebuffer_info fb_info = get_framebuffer_info("/dev/fb0"); std::cout << "xres virtua" << fb_info.xres_virtual << std::endl; std::cout << "bits per pixel" << fb_info.bits_per_pixel << std::endl; cap.open(0); if (!cap.isOpened()) { std::cerr << "Could not open video device." << std::endl; return 1; } std::cout << "Successfully opened video device." << std::endl; std::cout << "Display resolution:" << fb_info.xres << "x" << fb_info.yres << std::endl; cap.set(cv::CAP_PROP_FRAME_WIDTH, frame_width); cap.set(cv::CAP_PROP_FRAME_HEIGHT, frame_height); cap.set(cv::CAP_PROP_FPS, frame_rate); std::ofstream ofs("/dev/fb0"); cv::Mat frame; cv::Mat trams_temp_fream; cv::Mat yuv_frame; while (true) { cap >> frame; if (frame.depth() != CV_8U) { std::cerr << "Not 8 bits per pixel and channel." << std::endl; } else if (frame.channels() != 3) { std::cerr << "Not 3 channels." << std::endl; } else { //cv::transpose(frame, frame); //cv::flip(frame, frame, 0); cv::resize(frame, frame, cv::Size(fb_info.xres, fb_info.yres)); int framebuffer_width = fb_info.xres_virtual; int framebuffer_depth = fb_info.bits_per_pixel; cv::Size2f frame_size = frame.size(); cv::Mat framebuffer_compat; switch (framebuffer_depth) { case 16: cv::cvtColor(frame, framebuffer_compat, cv::COLOR_BGR2BGR565); break; case 32: std::vector<cv::Mat> split_bgr; cv::split(frame, split_bgr); split_bgr.push_back(cv::Mat(frame_size, CV_8UC1, cv::Scalar(255))); cv::merge(split_bgr, framebuffer_compat); break; } ofs.seekp(0); ofs.write(reinterpret_cast<char*>(framebuffer_compat.ptr(0)), framebuffer_compat.total() * framebuffer_compat.elemSize()); usleep(1000000 / frame_rate); } } } -

opencv图像处理
图像滤波 图像的滤波核心是使用一个小的矩阵(滤波器或卷积核)在图像上进行滑动卷积,将计算得到的结果作为目标像素的值。 均值滤波 cv::blur(InputArray src, OutputArray dst, Size ksize, Point anchor = Point(-1,-1), int borderType = BORDER_DEFAULT); src:输入的原始图像,支持Mat格式 dst:经过滤波处理的图像 ksize:滤波器大小,通常为2D大小,表示滤波的宽度和高度。 anchor:锚点指定窗口内的参考点,默认是Point(-1,-1)表示窗口中心点 boarderType:边界类型,用来处理边界参数的外推方式。 cv::Mat src = cv::imread("image.jpg", cv::IMREAD_GRAYSCALE); cv::Mat dst; cv::blur(src, dst, cv::Size(3, 3)); // 3x3的均值滤波 高斯滤波 void cv::GaussianBlur( const cv::Mat& src, cv::Mat& dst, cv::Size ksize, double sigmaX, double sigmaY = 0, int borderType = cv::BORDER_DEFAULT ); sigmaX:X方向的标准差,决定模糊的程度,值越大,模糊效果越强。 sigmaY:Y方向的标准差,默认是0,表示与X方向相同。 cv::GaussianBlur(src, dst, cv::Size(5, 5), 0); // 5x5的高斯滤波 中值滤波 void medianBlur(InputArray src, OutputArray dst, int ksize); ksize: 滤波器窗口大小 示例 cv::medianBlur(src, dst, 5); // 5x5的中值滤波 示例 下面示例,将图片使用高斯噪音处理,然后再使用滤波器进行模糊,噪音就可以看起来过滤掉。 #include <fcntl.h> #include <fstream> #include <iostream> #include <linux/fb.h> #include <signal.h> #include <stdint.h> #include <sys/ioctl.h> #include <unistd.h> #include <opencv2/opencv.hpp> using namespace cv; using namespace std; void add_gaussian_noise(Mat& image, double mean, double stddev) { Mat noise(image.size(), image.type()); randn(noise, mean, stddev); image = image + noise; } void display_image(const Mat& image, int framebuffer_width = 720) { static std::ofstream ofs("/dev/fb0"); cv::Mat framebuffer; cv::cvtColor(image, framebuffer, cv::COLOR_BGR2BGRA); cv::Size2f frame_size = framebuffer.size(); for (int y = 0; y < frame_size.height; y++) { ofs.seekp(y * framebuffer_width * 4); ofs.write(reinterpret_cast<char*>(framebuffer.ptr(y)), frame_size.width * 4); } } int main(int, char**) { Mat image = imread("test1.jpg", IMREAD_COLOR); if (image.empty()) { cerr << "Error: Could not open or find the image!" << endl; return -1; } double mean = 2.0; double stddev = 30.0; add_gaussian_noise(image, mean, stddev); display_image(image); cv::imwrite("noise.jpg", image); usleep(1000 * 1000 * 2); Mat dst; cv::GaussianBlur(image, dst, cv::Size(3, 3), 1); //cv::medianBlur(image, dst, 5); //cv::blur(src, dst, cv::Size(3, 3)); display_image(dst); cv::imwrite("dst.jpg", dst); } 如下图,中间是加了噪声的,最后一张是通过高斯滤波处理之后的。 图像形态学 膨胀与腐蚀 膨胀操作会增加图像中的白色区域或前景区域,使得图像中的对象或结构变得更大。具体来说,它会将图像中的每个像素点扩展到其邻域像素中(根据结构元素的大小和形状)。这意味着如果结构元素的一部分重叠在一个前景区域内,该区域就会被扩展。使白色区域扩展,物体变大。 cv2.dilate(src, dst=None, kernel, anchor=(-1, -1), iterations=1, borderType=cv2.BORDER_CONSTANT, borderValue=0) iteration:膨胀迭代次数,越大效果越明显 borderType:边界填充类型 borderValue:边界填充值,默认0是黑色 cv::Mat kernel = cv::getStructuringElement(cv::MORPH_RECT, cv::Size(3, 3)); //创建一个3*3的矩形结构元素 cv::dilate(src, dst, kernel); 腐蚀操作的效果与膨胀相反,它会减少图像中的白色区域或前景区域,使得图像中的对象变得更小。腐蚀操作会检查每个像素的邻域,如果邻域内的所有像素都是前景像素(白色),该像素才保持前景,否则变为背景(黑色)。使白色区域收缩,物体变小。 cv::Mat kernel = cv::getStructuringElement(cv::MORPH_RECT, cv::Size(3, 3)); cv::erode(src, dst, kernel); 以下是示例 #include <fcntl.h> #include <fstream> #include <iostream> #include <linux/fb.h> #include <signal.h> #include <stdint.h> #include <sys/ioctl.h> #include <unistd.h> #include <opencv2/opencv.hpp> void display_image(const cv::Mat& image, int framebuffer_width = 720) { static std::ofstream ofs("/dev/fb0"); if (!ofs) { std::cerr << "Error: Could not open framebuffer device!" << std::endl; return; } cv::Mat framebuffer; if (image.channels() == 1) { cv::cvtColor(image, framebuffer, cv::COLOR_GRAY2BGRA); } else if (image.channels() == 3) { cv::cvtColor(image, framebuffer, cv::COLOR_BGR2BGRA); } else if (image.channels() == 4) { image.copyTo(framebuffer); } else { std::cerr << "Error: Unsupported image format!" << std::endl; return; } cv::Size2f frame_size = framebuffer.size(); if (frame_size.width > framebuffer_width) { // 计算新的宽高,保持图像的纵横比 float aspect_ratio = frame_size.height / frame_size.width; int newWidth = framebuffer_width; int newHeight = static_cast<int>(newWidth * aspect_ratio); // 调整图像大小 cv::Mat resizedImage; cv::resize(framebuffer, resizedImage, cv::Size(newWidth, newHeight)); framebuffer = resizedImage; frame_size = resizedImage.size(); } for (int y = 0; y < frame_size.height; y++) { ofs.seekp(y * framebuffer_width * 4); ofs.write(reinterpret_cast<char*>(framebuffer.ptr(y)), frame_size.width * 4); } } int main(int, char**) { cv::Mat image = imread("test1.jpg", cv::IMREAD_COLOR); if (image.empty()) { std::cerr << "Error: Could not open or find the image!" << std::endl; return -1; } double mean = 2.0; double stddev = 30.0; display_image(image); usleep(1000 * 1000 * 1); cv::Mat dst; cv::Mat kernel = cv::getStructuringElement(cv::MORPH_RECT, cv::Size(5, 5)); cv::dilate(image, dst, kernel); display_image(dst); usleep(1000 * 1000 * 1); cv::erode(image, dst, kernel); display_image(dst); } 阈值化 阈值(Thresholding)是一种常见的图像分割方法,用于将灰度图像转换为二值图像。通过设置一个阈值,将像素值高于该阈值的区域设为白色(255),低于阈值的区域设为黑色(0),从而简化图像内容,便于后续处理。 二值化阈值:二值化是将图像中的像素值根据设定的阈值分为两类,通常用于简单的图像分割。 cv::threshold(src, dst, thresh, maxval, type); 示例:cv::threshold(src, dst, 127, 255, cv::THRESH_BINARY); thresh: 阈值,决定像素分类的分界线。 maxval:根据type选择,满足条件设置为最大值。 type: 阈值类型 自适应阈值:根据图像的局部区域动态计算阈值,适用于光照不均匀的图像。 cv::adaptiveThreshold( src, dst, maxValue, adaptiveMethod, thresholdType, blockSize, C); maxVaule:二值化的最大值,一般为255 adaptiveMethod: ADAPTIVE_THRESH_MEAN_C是使用邻域的均值作为阈值,ADAPTIVE_THRESH_GAUSSIAN_C :使用邻域的加权均值(高斯加权)作为阈值。 thresholdType:阈值类型,通常使用 THRESH_BINARY 或 THRESH_BINARY_INV。 blockSize:邻域的大小,必须是奇数(例如 3 , 5 , 7 , ...),该窗口在图像上滑动。 C:调整值,用于从计算的阈值中减去。调整结果的灵敏度。 cv::adaptiveThreshold(src, dst, 255, cv::ADAPTIVE_THRESH_MEAN_C, cv::THRESH_BINARY, 11, 2); 开闭运算、顶帽、黑帽 开运算:开运算是先进行腐蚀操作再进行膨胀操作。它通常用于去除小的噪点或小的物体,同时保留较大区域的结构。 闭运算:闭运算是先进行膨胀操作再进行腐蚀操作。它用于去除小的黑色区域(如小孔洞或空隙),并连接物体之间的细小裂缝。 顶帽:顶帽是开运算的结果与原图像之间的差异,主要用于提取比背景更亮的区域或小的亮点。 黑帽:黑帽是闭运算的结果与原图像之间的差异,主要用于提取比背景更暗的区域或小的暗点。 void cv::morphologyEx( InputArray src, OutputArray dst, int op, InputArray kernel, Point anchor = Point(-1, -1), int iterations = 1, int borderType = BORDER_CONSTANT, const Scalar&borderValue=morphologyDefaultBorderValue() ); kernel:结构元素,通常使用 cv::getStructuringElement() 生成。 op:形态学操作类型。 下面是op的类型 cv:MORPH_OPEN:开运算。 cv::MORPH_CLOSE:闭运算。 cv::MORPH_GRADIENT: 形态学梯度(膨胀 - 腐蚀),提取物体边缘。 cv::MORPH_TOPHAT :顶帽运算(原图 - 开运算结果),提取比背景亮的区域。 cv::MORPH_BLACKHAT 黑帽运算(闭运算结果 - 原图),提取比背景暗的区域。 示例 示例程序如下: int main(int, char**) { cv::Mat image = imread("test1.jpg", cv::IMREAD_GRAYSCALE); if (image.empty()) { std::cerr << "Error: Could not open or find the image!" << std::endl; return -1; } cv::Mat binary_img; cv::threshold(image, binary_img, 128, 255, cv::THRESH_BINARY); cv::Mat kernel = cv::getStructuringElement(cv::MORPH_RECT, cv::Size(5, 5)); cv::Mat dst; cv::Mat opened_img, closed_img, tophat_img, blackhat_img; cv::morphologyEx(binary_img, opened_img, cv::MORPH_OPEN, kernel); cv::morphologyEx(binary_img, closed_img, cv::MORPH_CLOSE, kernel); cv::morphologyEx(binary_img, tophat_img, cv::MORPH_TOPHAT, kernel); cv::morphologyEx(binary_img, blackhat_img, cv::MORPH_BLACKHAT, kernel); display_image(image); usleep(1000 * 1000 * 2); display_image(binary_img); usleep(1000 * 1000 * 2); display_image(closed_img); usleep(1000 * 1000 * 2); display_image(tophat_img); usleep(1000 * 1000 * 2); display_image(blackhat_img); } 图像边缘检测 canny Canny边缘检测是一个多阶段的图像处理算法,用于提取图像中的边缘。它的目标是识别图像中强度变化较大的区域,即边缘 int main(void) { cv::Mat image = cv::imread("test1.jpg", cv::IMREAD_GRAYSCALE); if (image.empty()) { std::cerr << "Error: Could not open image!" << std::endl; return -1; } // 进行 Canny 边缘检测 cv::Mat edges; cv::Canny(image, edges, 100, 200); // 低阈值 100,高阈值 200 display_image(edges); return 0; } 下面是处理的前后效果。 霍夫变换 霍夫变换(Hough Transform)是一种用于检测图像中的几何形状(如直线、圆等)的方法。它主要用于图像中的特征检测,特别是在噪声较大的图像中,可以有效地进行形状的识别。霍夫变换的基本思想是将图像中的边缘点通过一种数学映射,转化到参数空间,然后在参数空间中寻找对应的曲线(或直线、圆等)。 霍夫线变换: 检测线。 cv2.HoughLinesP(image, rho, theta, threshold, minLineLength, maxLineGap) image: 输入图像,通常是经过边缘检测(如 Canny 边缘检测)后的二值图像。 rho: 直线距离精度,单位是像素,通常设置为 1。 theta: 角度精度,单位是弧度,通常设置为 np.pi / 180(即 1°)。 threshold: 最小投票数,当某一候选直线在参数空间中的投票数大于此阈值时,认为检测到直线。 minLineLength: 最小直线长度。只有长度大于该值的直线才会被返回。 maxLineGap: 最大直线间隙。如果两段直线之间的间隙小于该值,则认为它们是同一条直线的两部分 int main(void) { cv::Mat img = cv::imread("test1.jpg"); if (img.empty()) { std::cerr << "Error: Could not open image!" << std::endl; return -1; } // 图像预处理:边缘检测 cv::Mat edges; cv::Canny(img, edges, 50, 150); // 使用 Canny 边缘检测 display_image(edges); usleep(1000 * 1000); // 使用 HoughLinesP 进行霍夫变换(概率霍夫变换) std::vector<cv::Vec4i> lines; cv::HoughLinesP(edges, lines, 1, CV_PI / 180, 50, 50, 10); // 参数为 (边缘图像, 输出的直线, ρ精度, θ精度, 阈值, 最小线段长度, 最大线段间隙) // 绘制检测到的直线 cv::Mat result = img.clone(); //cv::cvtColor(result, result, cv::COLOR_GRAY2BGR); // 将灰度图转为彩色图以显示彩色直线 for (size_t i = 0; i < lines.size(); i++) { cv::Vec4i l = lines[i]; cv::line(result, cv::Point(l[0], l[1]), cv::Point(l[2], l[3]), cv::Scalar(255, 0, 0), 2); // 绘制直线 } display_image(result); return 0; } 上面的示例中,先使用canny进行边缘处理,然后送入到霍夫变换中进行检测,最后绘制成直线。下面是检测后的效果。 霍夫圆变换: 检测圆。 cv2.HoughCircles(image, method, dp, minDist, param1, param2, minRadius, maxRadius) image: 输入图像,通常是灰度图像。 method: 霍夫变换的检测方法。对于 HoughCircles,一般使用 cv2.HOUGH_GRADIENT。 dp: 分辨率反比,表示霍夫空间的分辨率与图像分辨率的比例。通常设置为 1。 minDist: 设定圆心之间的最小距离,防止检测到相互靠得太近的圆。 param1: 边缘检测的高阈值(Canny 边缘检测的高阈值)。 param2: 圆的中心检测阈值,较小的值会检测到更多的圆,较大的值会检测较少的圆。 minRadius: 最小圆半径(单位:像素)。 maxRadius: 最大圆半径(单位:像素)。 int main(void) { cv::Mat img = cv::imread("test1.jpg"); if (img.empty()) { std::cerr << "Error: Could not open image!" << std::endl; return -1; } // 进行边缘检测 cv::Mat edges; cv::Canny(img, edges, 50, 150); display_image(edges); usleep(1000 * 1000); // 存储检测到的圆 std::vector<cv::Vec3f> circles; // 使用霍夫圆变换检测圆 cv::HoughCircles(edges, circles, cv::HOUGH_GRADIENT, 1, 23, 80, 52, 27, 100); // 在原图上绘制检测到的圆 cv::Mat result = img.clone(); for (size_t i = 0; i < circles.size(); i++) { cv::Point center(cvRound(circles[i][0]), cvRound(circles[i][1])); int radius = cvRound(circles[i][2]); // 绘制圆心 cv::circle(result, center, 3, cv::Scalar(0, 255, 0), -1); // 绘制圆 cv::circle(result, center, radius, cv::Scalar(255, 0, 0), 3); } display_image(result); return 0; } 同样是先使用canny检测进行处理,然后再使用霍夫圆进行检测圆,最后试用cv::circle进行绘制。 -

opencv基础操作
图像的读取和显示 读写图像 cv::Mat image = cv::imread("image.jpg", cv::IMREAD_COLOR); 使用imread函数读取图像,第一个参数是图像文件的路径,第二个参数是解释图像的颜色和格式(如彩色图像、灰度图像等)。第二个参数可省略,默认是cv::IMREAD_COLOR,以彩色图像读取。 cv::imwrite("output.jpg", image); 使用imwrite存储图像。 显示 使用imshow基于图像用户界面的显示方式,这种方式用于桌面的计算机,直接在屏幕上展示图像。 cv::imshow("Window title", image); cv::waitKey(0); // 等待按键按下 通过/dev/fb0节点写入,这种方式一般应用在嵌入式平台上,写入屏幕的驱动中。 std::ofstream ofs("/dev/fb0"); cv::Mat framebuffer; 定义一个存储图像像素数据的容器 cv::cvtColor(frame, framebuffer, cv::COLOR_BGR2BGR565); 将图像格式进行转换为与驱动支持的格式BGR565 ofs.write(reinterpret_cast<char*>(framebuffer.ptr(0)), framebuffer.total() * framebuffer.elemSize()); //现将framebuffer强制转换为char*格式,确保内存数据按字节进行处理。 //framebuffer.total()返回的是像素总元素数量,如果framebuffer是多通道,那就返回总数 //framebuffer.elemSize()返回的是每个像素字节大小。 //需要注意的是使用一次性写入,要注意fb的位置,每次写需要重新定位 还有另外一种写法,每一行每一行的刷新 cv::Size2f frame_size = frame.size(); cv::cvtColor(frame, framebuffer_compat, cv::COLOR_BGR2BGR565); for (int y = 0; y < frame_size.height; y++) { ofs.seekp(y * framebuffer_width * 2); //定位一行的位置,framebuffer_width是宽,即每行多少个像素 //*2是每个像素多少个字节,BGR565是2个字节。 ofs.write(reinterpret_cast<char*>(framebuffer_compat.ptr(y)), frame_size.width * 2); //写入一行数据,一行的数据量为frame_size.width * 2 } 下面是封装的示例函数 void display_image(const cv::Mat& image, int framebuffer_width = 720) { static std::ofstream ofs("/dev/fb0"); if (!ofs) { std::cerr << "Error: Could not open framebuffer device!" << std::endl; return; } cv::Mat framebuffer; if (image.channels() == 1) { cv::cvtColor(image, framebuffer, cv::COLOR_GRAY2BGRA); } else if (image.channels() == 3) { cv::cvtColor(image, framebuffer, cv::COLOR_BGR2BGRA); } else if (image.channels() == 4) { image.copyTo(framebuffer); } else { std::cerr << "Error: Unsupported image format!" << std::endl; return; } cv::Size2f frame_size = framebuffer.size(); if (frame_size.width > framebuffer_width) { // 计算新的宽高,保持图像的纵横比 float aspect_ratio = frame_size.height / frame_size.width; int newWidth = framebuffer_width; int newHeight = static_cast<int>(newWidth * aspect_ratio); // 调整图像大小 cv::Mat resizedImage; cv::resize(framebuffer, resizedImage, cv::Size(newWidth, newHeight)); framebuffer = resizedImage; frame_size = resizedImage.size(); } for (int y = 0; y < frame_size.height; y++) { ofs.seekp(y * framebuffer_width * 4); ofs.write(reinterpret_cast<char*>(framebuffer.ptr(y)), frame_size.width * 4); } } 示例 int main() { cv::Mat test_image = cv::imread("test.jpg"); if (test_image.empty()) { std::cerr << "Could not open the image" << std::endl; return -1; } std::ofstream ofs("/dev/fb0"); if (!ofs.is_open()) { std::cerr << "Failed to open framebuffer device." << std::endl; return -1; } // 将 BGR 图像转换为 BGRA 格式(RGB8888) cv::Mat framebuffer; cv::cvtColor(test_image, framebuffer, cv::COLOR_BGR2BGRA); ofs.write(reinterpret_cast<char*>(framebuffer.ptr(0)), framebuffer.total() * framebuffer.elemSize()); return 0; } 几何变换 这里的变换指的是缩放、旋转、平移、翻转。 裁剪与缩放 缩放 cv::Mat resizedImage; cv::resize(image, resizedImage, cv::Size(newWidth, newHeight)); 裁剪 Rect roi(100, 100, 200, 200); // (x, y, width, height) //先于x,y坐标开始,再按照width,height定义一个矩形框。 Mat croppedImage = image(roi); //将矩形框作用在image上,得到一个新的图像croppedImage 旋转 // cv::Point2f用于表示二维浮点坐标的类,下面是计算旋转中心点。 cv::Point2f center(image.cols / 2.0, image.rows / 2.0); // 用于计算二维旋转的仿射变换矩阵,45是旋转角度,1.0是缩放比例。 cv::Mat rotationMatrix = cv::getRotationMatrix2D(center, 45.0, 1.0); // 声明存储旋转后图像的变量 cv::Mat rotatedImage; // 执行仿射变换进行图像旋转 cv::warpAffine(image, rotatedImage, rotationMatrix, image.size()); 翻转 cv::Mat flippedImage; cv::flip(image, flippedImage, 1); // 1表示水平翻转,0表示垂直翻转 颜色变换 图像的颜色空间包括RGB、灰度和HSV等。 RGB:RGB是最常见的颜色空间,表示红、绿、蓝三个通道。 灰度:灰度图像只有一个通道,表示亮度。 HSV:HSV颜色空间表示色调(Hue)、饱和度(Saturation)和亮度(Value)。 颜色空间转换 RGB转灰度 cv::Mat grayImage; cv::cvtColor(image, grayImage, cv::COLOR_BGR2GRAY); RGB转HSV cv::Mat hsvImage; cv::cvtColor(image, hsvImage, cv::COLOR_BGR2HSV); RGB转RGB565 cv::Mat rgb565Image; cv::cvtColor(rgb565Image, framebuffer, cv::COLOR_BGR2BGR565); 通道分离 这里的通道指的是图像通道比如RGB的R/G/B 3个通道。通道分离的场景是分析每个颜色通道的像素值,比如在检测红色物体时,可以单独分析红色通道。另外还可以用做图像增强,对不同通道应用不同的增强算法,然后再合并。 通道分离 std::vector<cv::Mat> channels; //分离出的通道存储到channels中 cv::split(image, channels); 通道合并 cv::Mat mergedImage; cv::merge(channels, mergedImage); 示例代码 int main() { cv::Mat test_image = cv::imread("test.jpg"); if (test_image.empty()) { std::cerr << "Could not open the image" << std::endl; return -1; } double angle = 90; // 计算旋转中心点 cv::Point2f center(test_image.cols / 2.0, test_image.rows / 2.0); // 计算旋转矩阵 cv::Mat rotationMatrix = cv::getRotationMatrix2D(center, angle, 1.0); // 声明存储旋转后图像的变量 cv::Mat rotatedImage; // 执行仿射变换进行图像旋转 cv::warpAffine(test_image, rotatedImage, rotationMatrix, test_image.size()); std::ofstream ofs("/dev/fb0"); if (!ofs.is_open()) { std::cerr << "Failed to open framebuffer device." << std::endl; return -1; } // 将 BGR 图像转换为 BGRA 格式(RGB8888) cv::Mat framebuffer; cv::cvtColor(rotatedImage, framebuffer, cv::COLOR_BGR2BGRA); ofs.write(reinterpret_cast<char*>(framebuffer.ptr(0)), framebuffer.total() * framebuffer.elemSize()); return 0; } 总结 本章节总结opencv操作常用的数据结构。 Mat Mat对象的用途主要为存储图像、创建和操作多维矩阵。Mat数据类型分为两部分:信息头+指向像素数据的矩阵指针,信息头存储的是图像的尺寸、存储方法、存储地址。指向像素的矩阵指针为字面意思,即指向存储所有像素值的矩阵指针。 Mat A, C; //只创建信息头 A = imread(argv[1], IMREAD_COLOR); //为矩阵开辟内存空间。 Mat B(A); // Use the copy constructor C = A; // Assignment operator 如果在读取图像的时候只想获取图像中的部分图像(感兴趣的区域ROI),可以使用Rect和Range来标中数据。 Mat D (A, Rect(10, 10, 100, 100) ); // using a rectangle Mat E = A(Range::all(), Range(1,3)); // using row and column boundaries 其中Rect(10,10,100,100)前两位是坐标,后两位指定宽高,示例如下。 Range::all()选中所有的行,Range(1,3)选中1~3列。 Mat对象作为通用矩阵类和图像容器,容器中存储的是原始的像素值。在opencv中描述这些像素值有专门的数据格式。 Mat Img(640, 640, CV_8UC3); 上述中640*640大小的图像,存储的数据类型是CV_U8C3,这里的CV_U8C3格式为基本数据类型+通道数。"CV_"表示前缀,"8"表示每个像素值的位深比特数,有8/16/32/64bits,"U"表示数据类型为无符号,"C3"表示通道数RGB。关于通道一般有几种,示例如下: 1通道:灰度图像 3通道:RGB通道,图像由红、绿、蓝三色组成。 4通道:在RGB通道基础上,加一个透明通道。 Scalar Scalar用于表示颜色或像素的值,他是一个模板类,存储了4个值,每个值代表图像的颜色通道,如BGR或HSV。 template<typename _Tp> class Scalar_ { public: _Tp val[4]; // 颜色值,最多支持四个通道 .... }; cv::Scalar(0, 0, 255); // 红色 BGR 颜色,表示 (蓝色 = 0, 绿色 = 0, 红色 = 255) cv::Scalar(255, 0, 0); // 蓝色 BGR 颜色,表示 (蓝色 = 255, 绿色 = 0, 红色 = 0) cv::Scalar(0, 255, 0); // 绿色 BGR 颜色,表示 (蓝色 = 0, 绿色 = 255, 红色 = 0) cv::Scalar(0, 255, 0, 128); // 半透明绿色 cv::Scalar(255, 0, 0, 255); // 完全不透明的蓝色 Size Size类用来表示图像的大小、矩阵的尺寸。 class Size { public: Size(); Size(int _width, int _height); Size(double _width, double _height); int width; // 图像宽度 int height; // 图像高度 }; 下面是常用的用法。 设置图像的尺寸 cv::Mat image = cv::imread("image.jpg"); cv::Size new_size(800, 600); // 新的尺寸 cv::resize(image, image, new_size); // 将图像调整为新尺寸 获取图像的尺寸 cv::Mat image = cv::imread("image.jpg"); cv::Size image_size = image.size(); // 获取图像尺寸 创建一个尺寸大小的矩阵 cv::Mat mat(cv::Size(400, 300), CV_8UC1); // 创建一个大小为 400x300 的单通道图像 cvtColor cvtColor用于颜色空间的转化,图像的颜色空间一般有RGB,BGR(RGB存储顺序的不同),HSV,Lab等,其可以将图像从一种颜色空间变换为另一种颜色空间。 cv::Mat cv::cvtColor(const cv::Mat& src, cv::Mat& dst, int code, int dstCn = 0); src: 输入图像 dst:输出图像 code:指定转化格式,如 cv::COLOR_BGR2GRAY,cv::COLOR_BGR2HSV。 dstCn:输出通道数,如果是0,表示通道数与目标颜色空间通道匹配。 RGB转BGR cv::Mat src = cv::imread("image.jpg"); // 读取 RGB 图像(如果图像是 RGB 格式的话) cv::Mat bgr; cv::cvtColor(src, bgr, cv::COLOR_RGB2BGR); // 转换为 BGR 图像 HSB转BRG cv::Mat hsv = cv::imread("image_hsv.jpg"); // 读取 HSV 图像 cv::Mat bgr; cv::cvtColor(hsv, bgr, cv::COLOR_HSV2BGR); // 转换为 BGR 图像 BRG转灰度 cv::Mat src = cv::imread("image.jpg"); // 读取 BGR 图像 cv::Mat gray; cv::cvtColor(src, gray, cv::COLOR_BGR2GRAY); // 转换为灰度图 -
优化算法
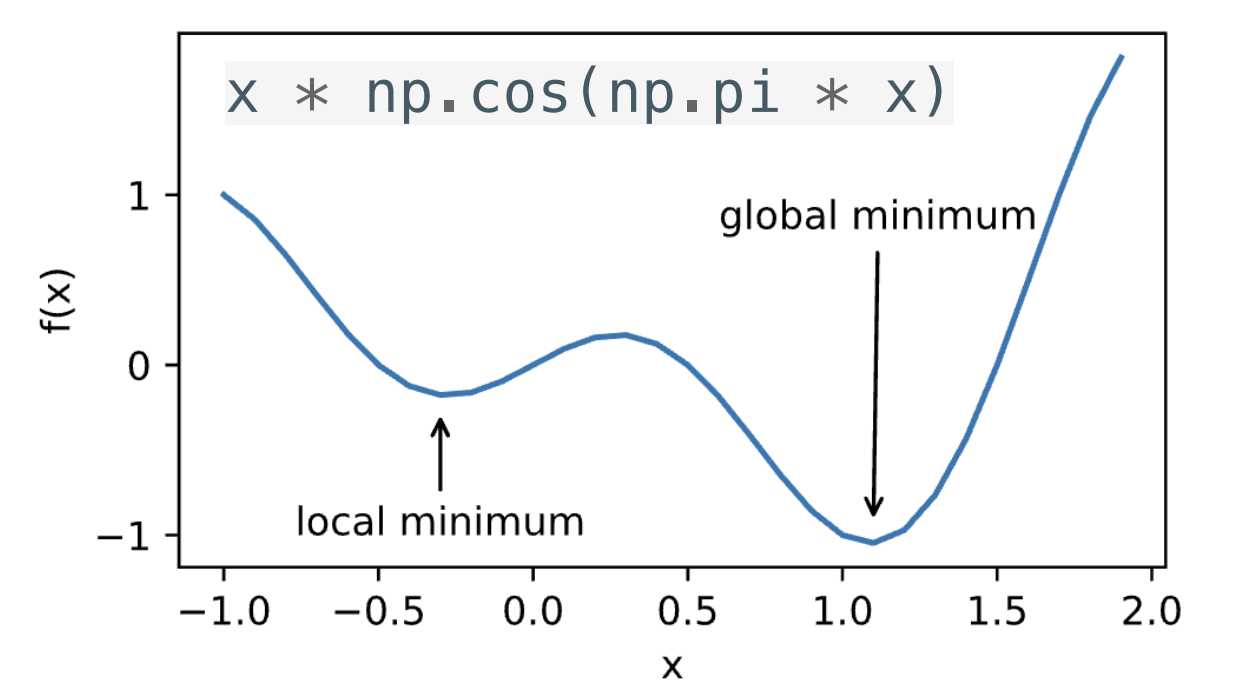
局部最小与全局最小 对应任何目标函数f(x),当然这里的目标函数可以是损失函数。如果在x处对应的f(x)小于x附近任意点的f(x),那么f(x)是局部最小的。如果f(x)在x处的值是整个域中目标函数的最小值,那么f(x)是全局最小值。 除了局部最优解外,鞍点也是梯度为0的区域。什么是鞍点了?如下图。 在深度学习模型训练中,通常往往会有许多局部最优解或鞍点,要解决这种局部最优解需要一定程度的噪音才能使参数跳出局部最小值,实际上使用小批量随机梯度下降也可以将参数从局部极小值中跳出。 梯度下降(gd) 对于多变量的输入$\mathbf{x} = [x_1, x_2, \ldots, x_d]^\top$的情况。它的梯度也是多元的,是一个由$d$个偏导数组成的向量: $$\nabla f(\mathbf{x}) = \bigg[\frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \ldots, \frac{\partial f(\mathbf{x})}{\partial x_d}\bigg]^\top$$ 梯度中的每个偏导数元素$\partial f(\mathbf{x})/\partial x_i$代表了当输入$x_i$时$f$在$\mathbf{x}$处的变化率。最陡下降的方向由负梯度$-\nabla f(\mathbf{x})$得出。选择合适的学习率$\eta > 0$来生成典型的梯度下降算法: $$\mathbf{x} \leftarrow \mathbf{x} - \eta \nabla f(\mathbf{x})$$ 假设一个目标函数$f(\mathbf{x})=x_1^2+2x_2^2$,并有二维向量$\mathbf{x} = [x_1, x_2]^\top$作为输入,标量作为输出。则梯度$\nabla f(\mathbf{x}) = [2x_1, 4x_2]^\top$给出。下面是梯度从[-5,-2]开始进行下降。 注意,在实际训练时,如果f(x)是损失函数,那么x就是参数,通常对应的是w。 随机梯度下降(sgd) 在深度学习中,在训练数据时,有很多样本,按照前面的梯度下降方法,那么对于多个样本的损失我们可以使用平均值来表示。给定$n$个样本的训练数据集,我们假设$f_i(\mathbf{w})$是关于索引$i$的训练样本的损失函数,其中$\mathbf{w}$是参数向量,我们得到损失函数为: $$f(\mathbf{w}) = \frac{1}{n} \sum_{i = 1}^n f_i(\mathbf{w})$$ $\mathbf{w}$的目标函数的梯度计算为 $$\nabla f(\mathbf{w}) = \frac{1}{n} \sum_{i = 1}^n \nabla f_i(\mathbf{w})$$ 如果使用梯度下降法,每计算一次梯度,需要对所有的样本做计算求平均,如果每个自变量迭代的计算代价为$\mathcal{O}(n)$,它随$n$线性增长。这样的方法虽然计算梯度准确性高,但是当训练数据集较大时,每次迭代的梯度下降计算代价将较高。 随机梯度下降(SGD)就是要降低计算量,在计算梯度时,不要对所有样本进行计算,而是在随机梯度下降的每次迭代中,对数据样本随机均匀采样一个索引$i$,也就是只取一个样本计算计算梯度, 其中$i\in{1,\ldots, n}$,并计算梯度$\nabla f_i(\mathbf{w})$以更新$\mathbf{w}$: $$\mathbf{w} \leftarrow \mathbf{w} - \eta \nabla f_i(\mathbf{w}),$$ 其中$\eta$是学习率。可以看到,每次迭代的计算代价从梯度下降的$\mathcal{O}(n)$降至常数$\mathcal{O}(1)$。此外,我们要强调,随机梯度$\nabla f_i(\mathbf{w})$是对完整梯度$\nabla f(\mathbf{w})$的无偏估计,因为 $$\mathbb{E}i \nabla f_i(\mathbf{w}) = \frac{1}{n} \sum{i = 1}^n \nabla f_i(\mathbf{w}) = \nabla f(\mathbf{w}).$$ 这意味着,平均而言,随机梯度是对梯度的良好估计。 总结一下,梯度下降使用全量数据计算梯度更新参数,适合小数据集,而随机梯度下降每次使用一个样本更新,适合大数据集。 小批量随机梯度下降(minibatch-sgd) 使用随机梯度下降只取一个样本,虽然降低了计算难度,但是如果样本差异较大时梯度波动大,收敛不稳定,而且不能做并行计算。对梯度下降和随机梯度下降做一个折中,对于批量输入样本,我们分为多个小批量,计算梯度是我们使用小批量来计算梯度,这样相对梯度下降不是算全部,同时对于如果是多GPU并行计算的,多个小批量可以并行, $ (w, b) \leftarrow (w, b) - \frac{\eta}{|B|} \sum_{i \in B} \nabla_{(w, b)} \ell^{(i)}(w, b) $ 公式中的$B$是抽样的小批量,是固定数量的训练样本。梯度公式也可以表示为如下,其中$Xi$是第$i$个输入样本,$W$是参数: $$ \mathbf{g}{t, t-1} = \frac{\partial \mathbf{W}}{|\mathcal{B}_t|} \sum{i \in \mathcal{B}t} f(\mathbf{X}{i}, \mathbf{W}_{t-1}) $$ 总结一下,梯度下降使用全量数据更新参数,随机梯度下降每次使用一个样本更新,而小批量随机梯度下降则每次使用一小部分样本更新,介于二者之间。 动量法(momentum) 动量法是深度学习中一种常用的参数优化方法,旨在加速梯度下降优化过程,特别是在处理高维数据时能够帮助模型更快地收敛。其核心思想借鉴了物理中的动量概念,目的是避免在梯度下降过程中由于局部震荡而导致的效率低下。 在标准的梯度下降中,更新参数的方式是直接沿着梯度的方向调整参数: $$ w_t = w_{t-1} - \eta \nabla_w L(w_{t-1}) $$ 其中: - $w_t$ 是当前的参数, - $\eta$ 是学习率, - $\nabla_w L(w_{t-1})$ 是当前参数的梯度。 动量法的思想是,不仅考虑当前的梯度,还要考虑前几次更新的方向和大小,从而引入“惯性”来加速优化过程,避免参数更新过程中出现震荡。具体的更新规则如下: 首先,计算当前参数的梯度: $$ \nabla_w L(w) $$ 引入一个速度变量(momentum),根据上一次的速度和当前的梯度来计算新的速度: $$ v_t = \beta v_{t-1} + (1 - \beta) \nabla_w L(w) $$ 其中: - $\beta$ 是动量衰减因子,通常取值在 $[0, 1)$ 之间,表示前一次更新的影响程度, - $v_t$ 是当前的“速度”,表示参数更新的方向和大小。 用速度来更新参数: $$ w_t = w_{t-1} - \eta v_t $$ 其中: - $\eta$ 是学习率,控制更新的步长。 动量法有什么效果了? 加速收敛:动量法能够加速收敛过程,特别是在处理高维数据时,能够减少梯度下降中震荡的现象。 克服局部最小值:动量法有助于跳出局部最小值,帮助优化算法在复杂的损失函数中找到更优的解。 提高稳定性:动量法通过结合前几次的梯度信息,使得参数更新更平滑,避免了仅依赖当前梯度时可能出现的震荡。 动量法有什么不足? 参数选择:动量法的效果在不同任务中依赖于动量衰减因子 $\beta$ 和学习率 $\eta$ 的选择,可能需要多次调参才能找到最优的参数。 计算开销:相比于标准的梯度下降,动量法需要额外保存上一次的梯度信息,因此增加了一定的内存开销。 常见的动量法变种? Nesterov Accelerated Gradient (NAG):NAG 是动量法的一种改进方法,它在计算梯度时会考虑当前的速度,以更好地调整更新方向。 自适应动量法(Adam):Adam 优化器结合了动量法和自适应学习率的方法,广泛用于深度学习中,能够自动调整每个参数的学习率。 总结下,动量法是深度学习中常见的优化算法,通过引入前几次梯度的加权平均,帮助加速收敛,减少震荡,并有效地应对复杂的损失函数。在实际应用中,动量法常常和其他优化方法结合使用,如自适应学习率方法(Adam)等。 Adam adam是在动量法的基础上再加上自适应学习率,所谓自适应学习率就是根据历史梯队信息动态的调整。 想象一下你正在穿越一个复杂的地形,找到最低点,在道路平坦的地方你可以迈出大步,崎岖的地方减速这就是自适应调整学习率,同时你又保持一个动量,在你下一次动作时会有上一次的冲量,当转弯时会有上一次的动量也不至于一下偏差很远而错过。 Adam优化器通过计算梯度的一阶矩(即梯度的平均值)和二阶矩(即梯度的平方的平均值)来动态调整每个参数的学习率。具体的步骤如下: 首先计算一阶矩和二阶矩,对于每个参数$w$,Adam维护两个变量: 一阶矩 $m_t$(动量):梯度的指数加权平均。 二阶矩$v_t$(自适应学习率):梯度的平方的指数加权平均。 这两个变量分别更新如下: $m_t = \beta_1 m_{t-1} + (1 - \beta_1) \nabla_w L(w)$ $v_t = \beta_2 v_{t-1} + (1 - \beta_2) (\nabla_w L(w))^2$ $\nabla_w L(w)$ 是当前参数的梯度, $\beta_1$和 $\beta_2$是控制一阶矩和二阶矩衰减率的超参数,通常取值为 0.9 和 0.999。 由于在初始阶段一阶矩和二阶矩的估计偏向于零,Adam对这两个矩进行偏差修正:$\hat{m_t} = \frac{m_t}{1 - \beta_1^t}$,$\hat{v_t} = \frac{v_t}{1 - \beta_2^t}$ 最后,使用修正后的矩估计来更新参数:$w_t = w_{t-1} - \eta \frac{\hat{m_t}}{\sqrt{\hat{v_t}} + \epsilon}$。 $\eta$是学习率, $\epsilon$ 是一个小常数(如 $10^{-8}$),用来避免除以零的情况。 Adam有什么优点? 自适应学习率:Adam会自动调整每个参数的学习率,这样可以在训练过程中避免手动调整学习率的麻烦。 结合了动量法和自适应学习率:通过一阶矩和二阶矩的估计,Adam能够更有效地处理不同参数在训练过程中的变化,避免了梯度下降过程中出现的震荡。 适用于大规模数据和高维参数:Adam能够在处理大规模数据时稳定并高效地收敛,特别是在处理稀疏梯度(如自然语言处理任务)时表现尤为突出。 Adam有什么缺点? 超参数调整:尽管Adam是自适应的,但在某些情况下,仍然需要调整超参数(如学习率 $\eta$,$\beta_1$ 和 $\beta_2$)才能获得最好的训练效果。 可能导致过度拟合:在某些任务中,使用Adam优化器可能会导致模型的过度拟合,需要适当的正则化策略来避免。 Adam优化器通过结合动量法和自适应学习率调整的机制,能够加速模型训练过程,提高收敛速度,尤其适用于处理大规模数据和复杂的深度学习模型。 -
全连接层与卷积层参数计算
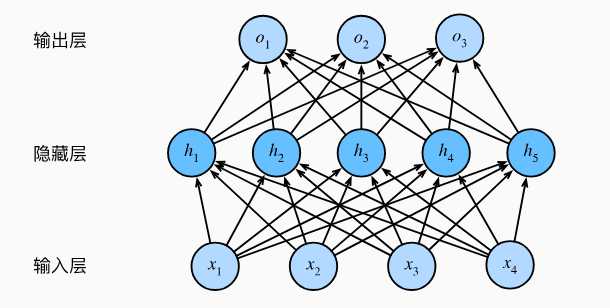
层的概念 在前面http://www.laumy.tech/2013.html有说明"层与块"概念,为了加深影响,本章再简要概括一下深度学习中常见的层。 在深度学习中,层(Layer)是神经网络的基本构建模块,负责对输入数据进行特定变换(如线性加权、非线性激活、特征提取等)。每一层接收输入数据,通过内部参数和计算规则生成输出,传递给下一层。常见的层有全连接层、激活函数层、卷积层、池化层、归一化层(Normalization Layer)、正则化(dropout)。当然层还可以自己定义。 全连接层 全连接层(Fully Connected Layer)是指当前层每个神经元均与前一层的所有神经元相,通过权重矩阵和偏置向量实现全局特征整合。全连接层计算公式为y=wx+b。其作用是将局部特征(如卷积层提取的边缘、纹理)映射为全局语义信息(如物体类别),常用于分类或回归任务的输出层。 下面是一个全连接层的结构。从上面的结构可以总结一下全连接层的参数计算公式,Params=(输入节点+1)×输出节点数,公式中的+1代表的是偏置项(bias)。 因此上图中的总参数量为:(4+1)*5 + (5+1)*3 = 25 + 18 = 43。 卷积层 卷积核是在输入数据上滑动,计算局部区域的加权和(如3×3窗口),其作用可以捕边缘、纹理、形态等基础特征。 卷积核的参数计算公式为,参数量=(卷积核高×卷积核宽×输入通道数+1)×输出通道数。上图示例中,输入2通道,输出1通道,所以参数量为2*2*2*1 = 8,这里没有考虑偏置bias。从这里可以看出,相对卷积层比全连接层参数很少很多。 -

计算机视觉
图像增广 什么是图像增广?图像增广(Image Augmentation)是通过对原始图像进行一系列随机变换(如旋转、裁剪、颜色调整等)生成多样化样本的数据增强技术,旨在扩充训练数据集、提升模型泛化能力。其核心逻辑是模拟真实场景中可能存在的多样性,使模型学习到更鲁棒的特征。 深度学习中泛化能力是模型对未见过的新数据的适应能力,其核心体现在从训练数据中学习通用规律而非简单记忆特例。应用图像增广可以随机改变训练样本可以减少模型对某些属性的依赖,从而提高模型的泛化能力。 d2l.set_figsize() img = d2l.Image.open('../img/cat1.jpg') d2l.plt.imshow(img); 常用的图像增广方法有翻转和裁剪、改变颜色等,大多数图像增广都是随机性,下面定义一个函数应用图像增广后显示的效果。 def apply(img, aug, num_rows=2, num_cols=4, scale=1.5): Y = [aug(img) for _ in range(num_rows * num_cols)] #for循环随机增强输出num_rows * num_cols个图像 #创建了一个列表Y,包含了num_rows * num_cols个增强后的图像 #aug(img)是对img应用增强操作。 d2l.show_images(Y, num_rows, num_cols, scale=scale) img:输入原始的图像 aug:输入的增强函数 num_rws: 显示增广后图像的行数。 num_cols: 显示增广后图像的列数。 scale:调整显示图像的缩放比例。 翻转和裁剪 翻转有左右翻转、上下翻转,翻转该不会改变对象的类别,下面看看效果。 apply(img, torchvision.transforms.RandomHorizontalFlip()) apply(img, torchvision.transforms.RandomVerticalFlip()) 除了翻转还可以随机裁剪。 shape_aug = torchvision.transforms.RandomResizedCrop( (200, 200), scale=(0.1, 1), ratio=(0.5, 2)) apply(img, shape_aug) 改变颜色 改变颜色可包括几个方面包括亮度、对比度、饱和度和色调。 color_aug = torchvision.transforms.ColorJitter( brightness=0.5, contrast=0.5, saturation=0.5, hue=0.5) apply(img, color_aug) 混合增强 在实际项目中,可以将多种图像增广方面混合起来,可以调用Compose来实现。 augs = torchvision.transforms.Compose([ torchvision.transforms.RandomHorizontalFlip(), color_aug, shape_aug]) apply(img, augs) 微调(fine-tuning) 微调是在一个预训练模型的基础上,针对特定任务或数据集进行进一步训练,以便使模型能够更好的使用新的数据和任务。微调的步骤如下: 在源数据上预训练源模型。 创建一个新的目标模型,将源模型上的所有设计及参数(除输出层外)复制到目标模型。 新的目标模型添加输出层,输出数是目标数据集中类别数,只随机初始化该输出的参数。 新的目标集上训练目标模型。输出层是从头训练,而其他层是根据源模型参数进行微调。 为什么要微调?因为一个新的模型训练很贵,不但需要重新标注数据集、训练,那既然已经有训练好的模型,我们为何不根据训练好的模型稍加调整,站在巨人的肩膀上了? 为什么可以微调了? 一般神经网络可以分成两块 特征提取: 将原始的像素变成容易线性分割的特征。 softmax回归:线性分类器做分类。 因此特征提取部分一般是通用做法,所以容易复用,我们只需要替换到softmax输出层重新训练即可。 微调中权重参数是怎么初始化的?对于特征提取部分直接复制原来预训练的模型,输出层因为是修改替换的,所以需要重新随机初始化进行训练。微调训练是一个目标数据集上的正常训练任务,但是使用更强的正则化,具体体现在使用更小的学习率和使用更少的数据迭代。预训练模型源数据集若远远复杂于新目标数据集,通常微调效果更好。 下面是使用ResNet-18作为源模型来进行微调概要示例。 pretrained_net = torchvision.models.resnet18(pretrained=True) #定义和初始化预训练模型,指定pretrained=True,表示自动下载预训练的模型参数。 pretrained_net.fc #.fc表示最后输出层即全连接层,先打印看看效果 # 打印结果:Linear(in_features=512, out_features=1000, bias=True) # 可以看到最后输出层是输入512,输出1000的全连接层 finetune_net.fc = nn.Linear(finetune_net.fc.in_features, 2) #我们将最后的全连接层修改为输入不变,但是输出为2的全连接层,表示只分类2个目标。 nn.init.xavier_uniform_(finetune_net.fc.weight); #对新定义的全连接层fc进行权重初始化,采用的是xavier均分布方法 train_fine_tuning(finetune_net, 5e-5) #使用新的模型进行训练。 微调是通过使用大数据上得到预训练好的模型来初始化模型权重来完成提升精度,使用微调通常速度更快、精度更高。 目标检测 目标检测或目标识别是用于识别图像中多个感兴趣的目标,不仅知道他们的类别,还需要知道他们在图像中的具体位置。 如上图,图中有个狗和猫,通过一个边缘框框起来,边缘框左上角坐标+右下角坐标即可定位。 锚框(anchor box) 目标检测既然要在图像中检测出感兴趣目标的位置(坐标),那么就需要遍历框住不同的区域来进行识别。目标检测算法会在输入图像中抽样大量区域,然后判断这些区域中是否包含我们感兴趣的目标,并调整区域边缘,从而更准确的预测目标的真实边界框。不同的模型抽样的方法不同,这里主要介绍的是以每个像素为中心,生成多个缩放比和宽高比不同的边界框,这些边界就称为锚框。 如何生成锚框了? 假设输入图像的高度是h,宽度是w。那么就以每个像素按照缩放比(scale)和宽高(aspect ratio)比,为中心生成不同形状的锚框,那么锚框的宽度和高度分别为[锚框的宽度和高度分别是$hs\sqrt{r}$和$hs/\sqrt{r}$。]。在实践中,如果按照缩放比和宽高比组合时,每个输入图像共有$whnm$个锚框,这样数量太庞大,计算复杂度会很高,因此只考虑包含s和r的组合。$(s_1, r_1), (s_1, r_2), \ldots, (s_1, r_m), (s_2, r_1), (s_3, r_1), \ldots, (s_n, r_1).$,这样对于整个输入图像,将生成$wh(n+m-1)$个锚框。 img = d2l.plt.imread('../img/catdog.jpg') h, w = img.shape[:2] print(h, w) X = torch.rand(size=(1, 3, h, w)) Y = multibox_prior(X, sizes=[0.75, 0.5, 0.25], ratios=[1, 2, 0.5]) # multibox_prior返回的形状是(批量大小,锚框的数量,4) Y.shape 输处: 561 728 torch.Size([1, 2042040, 4]) 可以看到运行后,锚框的数量是2042040。 d2l.set_figsize() bbox_scale = torch.tensor((w, h, w, h)) fig = d2l.plt.imshow(img) show_bboxes(fig.axes, boxes[250, 250, :, :] * bbox_scale, ['s=0.75, r=1', 's=0.5, r=1', 's=0.25, r=1', 's=0.75, r=2', 's=0.75, r=0.5']) 上面是画出坐标[250,250]像素点,取一些s/r值的锚框效果。 如何衡量锚框和真实目标边界框的相似性了,使用交并比IoU,即两个边界框相交面积与相并面积的比。给定集合$\mathcal{A}$和$\mathcal{B}$,他们的杰卡德系数是他们交集的大小除以他们并集的大小: $$J(\mathcal{A},\mathcal{B}) = \frac{\left|\mathcal{A} \cap \mathcal{B}\right|}{\left| \mathcal{A} \cup \mathcal{B}\right|}.$$ 交并比的取值范围是0~1:0表示两个边界无重合像素,1表示两个边界完成重合。 在实际训练中如何标注锚框了? 在实际训练中,我们将每个锚框视为一个训练样本,为了训练目标检测模型,我们为每个锚框的类别和偏移进行标签,类别是与锚框相关的目标类别,偏移是真实边界框相对锚框的偏移量。在预测的时候,首先每张图片生成多个锚框,预测所有锚框的类别和偏移量,根据预测的偏移量调整他们的位置以获得预测的边界框,最后输出符合条件的预测边界框。 在预测时,可能输出许多相似的具有明显重叠的预测边界框,他们都围绕同一个目标。为了简化输出,使用非极大值抑制合并属于同一目标的相似的预测边界框。非极大值抑制的主要原理时,进行比较每个预测边界框的置信度,具体使用IoU来比较选取最大值。 通过非极大抑制预测处理后的结果。 区域卷积神经网络 R-CNN R-CNN从图像中选取若干(如2000)提议区域(如锚框是一种选取方法),预测标注他们的类别和边界框(如偏移量),然后使用卷积神经网络对每个提议区域进行前向传播已抽取特征,根据特征来预测类别和边界框。 使用R-CNN一般使用的是预训练来的卷积网络来抽取图像特征,但是每个图像会选出上千个提议区域,每个提议区域都需要经过卷积计算,这样也要上千次的卷积神经网络前向传播来执行目标检测,因此这样速度会很慢。 Fast R-CNN R-CNN的性能瓶颈主要在于对每个提议区域,卷积神经网络的前向传播都是独立的,没有共享计算。而这些提议区域往往会有重叠,这样会导致特征抽取重复计算。而使用Faster-CNN则进行了改进。 与R-CNN相比,Fast R-CNN用来提取特征的卷积神经网络输入的是整个图像,而不是各个提议区域,这样就不用像R-CNN对每个提议区域都进行卷积神经网络计算。 而选择性搜索生成的n个提议区域还是不变,不同的是Fast R-CNN引入了兴趣区域汇聚层,将卷积神经网络的输出和提议区域作为输入,输出连接后的各个提议区域抽取特征。而R-CNN对提议区域的处理是直接输入到分类器中,输出目标类别。 总结一下Fast R-CNN有主要有两点: 经过卷积神经网络数量不同:R-CNN所有提议区域都需要经过,而Fast R-CNN只需要输入完整的一张图片。 提议区域用处不用:R-CNN将提议区域最终到分类器中输出目标类别,而Fast R-CNN将提议区域和经过卷积神经网络输出的特征当做输入给到兴趣区域池化层。 Faster R-CNN Fast R-CNN的缺点就是在选择性搜索中还是会生成大量的提议区域,为了优化这个提出了Faster R-CNN,提出将选择性搜索替换为区域提议网络,从而减少提议区域生成的数量。 如何减少提议区域生成的数量了? 主要使用了非极大值抑制,将提议区域中相似的或者说重叠比较多的剔除掉,这样输入到兴趣区域池化层就变少了。 Mask R-CNN 如果训练集标注了每个目标图像的像素级位置,那么可以使用Mask R-CNN。 从上图可以看出 Mask R-CNN相对Faster R-CNN变换点在后面部分,Mask R-CNN将兴趣区域汇聚层替换为兴趣区域对齐层。这里的对齐层就是通过在训练集上实现标注目标的具体位置通过双线性超值来的,这样就可以更精准保留特征图的信息,实现像素级的预测。可以理解为Faster R-CNN兴趣区域层还需要调参经过一堆网络计算预测,而这里通过实现标注的区域进一步确定了位置。 SSD 待补充 YOLO Faster R-CNN的检测分为两个阶段,首先区域提议网络(RPN)生成候选区域,接着在使用卷积神经网络对这些候选区域进行分类和边界框回归。 而yolo是单阶段检测,他将图像分成一个S*S的网格,每个网络预测多个边界框和相应类别的概率。YOLO一次性处理整个图像,直接进行目标分类和定位回归,速度相对较快。Faster R-CNN精度会更高一些,在复杂场景和多目标检测比较优越。而YOLO实时性、低延迟,但是精度偏低,但是随着YOLO的进化精度逐渐在提升。 语义分割 语义分割是对图像中的每个像素进行分类到特定类别中。与目标检测不同的是,目标检测是识别图像中的物体并定位其边界框,而语义分割是则对图像的每个像素进行标注,赋予每个像素一个表情。语义分割是像素级别的分类。语义分割的应用如图像处理背景虚化、智能驾驶路面分割。 语义分割和实例分割的区别是语音分割只对像素类别进行分类,而示例分割是在像素类别中对实例在区分,如下图所示。 最重要的语义分割数据集是Pascal VOC2012。 转置卷积 卷积不会增大原来的输入高宽,要么维持不变、要么减小。而转置卷积则可以用来增大输入高宽。 转置卷积可以认为是卷积的逆过程。 全卷积网络FCN 语义分割是对图像中的每个像素分类,通常输入的图像大小和输出图像的大小要一样,也就是说输出类别的预测与输入图像在像素级上是具有一一对应关系。 FCN是用来做语义分割最早的深度卷积神经网络之一,他使用转置卷积层来替换CNN最后的全连接层。 样式迁移 图像处理经常会遇到滤镜,而使用卷积神经网络,自动将一张图像的风格应用在另外一张图像上,即称为样式迁移。 如上图,将style image中的样式迁移到content image上,就得到一张合成图片。 最终的损失内容损失+样式损失,即总变成损失。也就是说训练的时候输出图像的内容要跟源图像的内容接近,而样式跟样式图片接近。 本文来自: <动手学深度学习 V2> 的学习笔记 -
现代卷积神经网络
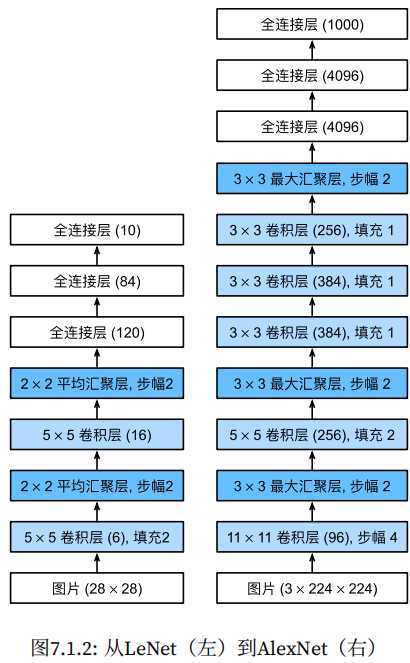
深度卷积神经网络AlexNet AlexNet相对LeNet的特点就是层数变得更深了,参数变得更多了。AlexNet由八层组成:五个卷积层、两个全连接隐藏层和一个全连接输出层。AlexNet使用ReLU而不是sigmoid作为其激活函数。 import torch from torch import nn from d2l import torch as d2l net = nn.Sequential( nn.Conv2d(1, 966, kernel_size=11, stride=4, padding=1), nn.ReLU(), nn.MaxPool2d(kernel_size=3, stride=2), nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(), nn.MaxPool2d(kernel_size=3, stride=2), nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(), nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(), nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(), nn.MaxPool2d(kernel_size=3, stride=2), nn.Flatten(), nn.Linear(6400, 4096), nn.ReLU(), nn ) X = torch.randn(1, 1, 224, 224) for layer in net: X=layer(X) print(layer.__class__.__name__,'output shape:\t',X.shape) 示例结果: Conv2d output shape: torch.Size([1, 96, 54, 54]) ReLU output shape: torch.Size([1, 96, 54, 54]) MaxPool2d output shape: torch.Size([1, 96, 26, 26]) Conv2d output shape: torch.Size([1, 256, 26, 26]) ReLU output shape: torch.Size([1, 256, 26, 26]) MaxPool2d output shape: torch.Size([1, 256, 12, 12]) Conv2d output shape: torch.Size([1, 384, 12, 12]) ReLU output shape: torch.Size([1, 384, 12, 12]) Conv2d output shape: torch.Size([1, 384, 12, 12]) ReLU output shape: torch.Size([1, 384, 12, 12]) Conv2d output shape: torch.Size([1, 256, 12, 12]) ReLU output shape: torch.Size([1, 256, 12, 12]) MaxPool2d output shape: torch.Size([1, 256, 5, 5]) Flatten output shape: torch.Size([1, 6400]) Linear output shape: torch.Size([1, 4096]) ReLU output shape: torch.Size([1, 4096]) Dropout output shape: torch.Size([1, 4096]) Linear output shape: torch.Size([1, 4096]) ReLU output shape: torch.Size([1, 4096]) Dropout output shape: torch.Size([1, 4096]) Linear output shape: torch.Size([1, 10]) AlexNet是更大更深的LeNet,比LeNet多了10倍的参数,260倍的计算复杂度。同时添加了丢弃法和ReLU。 使用块的网络VGG 通过AlexNet实践,添加更多的层使得模型的效果更好,但是要添加多少层了?是否有一些通用模版可以提供指导,VGG块就是解决这样的问题。将一些列的卷积层封装为一个块方便调用。 import torch from torch import nn from d2l import torch as d2l def vgg_block(num_convs, in_channels, out_channels): layers = [] for _ in range(num_convs): layers.append(nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1)) layers.append(nn.ReLU()) in_channels = out_channels layers.append(nn.MaxPool2d(kernel_size=2,stride=2)) return nn.Sequential(*layers) def vgg(conv_arch): conv_blks = [] in_channels = 1 # 卷积层部分 for (num_convs, out_channels) in conv_arch: conv_blks.append(vgg_block(num_convs, in_channels, out_channels)) in_channels = out_channels return nn.Sequential( *conv_blks, nn.Flatten(), # 全连接层部分 nn.Linear(out_channels * 7 * 7, 4096), nn.ReLU(), nn.Dropout(0.5), nn.Linear(4096, 4096), nn.ReLU(), nn.Dropout(0.5), nn.Linear(4096, 10)) conv_arch = ((1, 64), (1, 128), (2, 256), (2, 512), (2, 512)) net = vgg(conv_arch) X = torch.randn(size=(1, 1, 224, 224)) for blk in net: X = blk(X) print(blk.__class__.__name__,'output shape:\t',X.shape) 运行结果: Sequential output shape: torch.Size([1, 64, 112, 112]) Sequential output shape: torch.Size([1, 128, 56, 56]) Sequential output shape: torch.Size([1, 256, 28, 28]) Sequential output shape: torch.Size([1, 512, 14, 14]) Sequential output shape: torch.Size([1, 512, 7, 7]) Flatten output shape: torch.Size([1, 25088]) Linear output shape: torch.Size([1, 4096]) ReLU output shape: torch.Size([1, 4096]) Dropout output shape: torch.Size([1, 4096]) Linear output shape: torch.Size([1, 4096]) ReLU output shape: torch.Size([1, 4096]) Dropout output shape: torch.Size([1, 4096]) Linear output shape: torch.Size([1, 10]) VGG是使用可重复使用的卷积块来构建深度卷积神经网络,不同卷积块的个数和超参数可以得到不同复杂度的变种。 网络中的网络NiN 使用卷积层可以减少训练的参数。但从前面AlexNet或者VGG的示例中,卷积层后面全连接层参数是比较大的 LeNet: 1655*120 = 48K AlexNet: 25655*4096 = 26M VGG: 51277*4096 = 102M 哪有没有什么办法可以替换到全连接以减少参数?方法就是将全连接层替换为1*1的卷积层也可以起到全连接层的作用。 import torch from torch import nn from d2l import torch as d2l def nin_block(in_channels, out_channels, kernel_size, strides, padding): return nn.Sequential( nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding), nn.ReLU(), nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU(), nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU()) net = nn.Sequential( nin_block(1, 96, kernel_size=11, strides=4, padding=0), nn.MaxPool2d(3, stride=2), nin_block(96, 256, kernel_size=5, strides=1, padding=2), nn.MaxPool2d(3, stride=2), nin_block(256, 384, kernel_size=3, strides=1, padding=1), nn.MaxPool2d(3, stride=2), nn.Dropout(0.5), # 标签类别数是10 nin_block(384, 10, kernel_size=3, strides=1, padding=1), nn.AdaptiveAvgPool2d((1, 1)), # 将四维的输出转成二维的输出,其形状为(批量大小,10) nn.Flatten()) X = torch.rand(size=(1, 1, 224, 224)) for layer in net: X = layer(X) print(layer.__class__.__name__,'output shape:\t', X.shape) 运行结果: Sequential output shape: torch.Size([1, 96, 54, 54]) MaxPool2d output shape: torch.Size([1, 96, 26, 26]) Sequential output shape: torch.Size([1, 256, 26, 26]) MaxPool2d output shape: torch.Size([1, 256, 12, 12]) Sequential output shape: torch.Size([1, 384, 12, 12]) MaxPool2d output shape: torch.Size([1, 384, 5, 5]) Dropout output shape: torch.Size([1, 384, 5, 5]) Sequential output shape: torch.Size([1, 10, 5, 5]) AdaptiveAvgPool2d output shape: torch.Size([1, 10, 1, 1]) Flatten output shape: torch.Size([1, 10]) NiN块使用卷积层加两个1*1卷积层,整个架构没有全连接层,降低了参数的数量。 并行连结的网络GoogleNet 在goodLeNet,基本的卷积块称为Inception块,有四条并行路径组成。googleNet类似于滤波器的组合,可以用各种滤波器尺寸探索图像,不同大小的滤波器可以有效识别不同范围的图像细节。 import torch from torch import nn from torch.nn import functional as F from d2l import torch as d2l class Inception(nn.Module): # c1--c4是每条路径的输出通道数 def __init__(self, in_channels, c1, c2, c3, c4, **kwargs): super(Inception, self).__init__(**kwargs) # 线路1,单1x1卷积层 self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1) # 线路2,1x1卷积层后接3x3卷积层 self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1) self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1) # 线路3,1x1卷积层后接5x5卷积层 self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1) self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2) # 线路4,3x3最大汇聚层后接1x1卷积层 self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1) self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1) def forward(self, x): p1 = F.relu(self.p1_1(x)) p2 = F.relu(self.p2_2(F.relu(self.p2_1(x)))) p3 = F.relu(self.p3_2(F.relu(self.p3_1(x)))) p4 = F.relu(self.p4_2(self.p4_1(x))) # 在通道维度上连结输出 return torch.cat((p1, p2, p3, p4), dim=1) b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3), nn.ReLU(), nn.MaxPool2d(kernel_size=3, stride=2, padding=1)) b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1), nn.ReLU(), nn.Conv2d(64, 192, kernel_size=3, padding=1), nn.ReLU(), nn.MaxPool2d(kernel_size=3, stride=2, padding=1)) b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32), Inception(256, 128, (128, 192), (32, 96), 64), nn.MaxPool2d(kernel_size=3, stride=2, padding=1)) b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64), Inception(512, 160, (112, 224), (24, 64), 64), Inception(512, 128, (128, 256), (24, 64), 64), Inception(512, 112, (144, 288), (32, 64), 64), Inception(528, 256, (160, 320), (32, 128), 128), nn.MaxPool2d(kernel_size=3, stride=2, padding=1)) b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128), Inception(832, 384, (192, 384), (48, 128), 128), nn.AdaptiveAvgPool2d((1,1)), nn.Flatten()) net = nn.Sequential(b1, b2, b3, b4, b5, nn.Linear(1024, 10)) X = torch.rand(size=(1, 1, 96, 96)) for layer in net: X = layer(X) print(layer.__class__.__name__,'output shape:\t', X.shape) 运行结果: Sequential output shape: torch.Size([1, 64, 24, 24]) Sequential output shape: torch.Size([1, 192, 12, 12]) Sequential output shape: torch.Size([1, 480, 6, 6]) Sequential output shape: torch.Size([1, 832, 3, 3]) Sequential output shape: torch.Size([1, 1024]) Linear output shape: torch.Size([1, 10]) inception块用了4条有不同超参数的卷积层和池化层的路来抽取不同的信息,它主要的优点事模型参数小,计算复杂度第,googleNet用了9个Inception块,是第一个达到上百层的网络。 批量归一化 批量归一化(Batch Normalization,简称BN)是一种在训练神经网络时用于加速收敛、提高模型稳定性和提高性能的技术。它通过规范化每一层的输入,确保每一层的输入具有相同的分布,从而减少了不同层之间数据分布的变化,避免了梯度消失或爆炸问题。 具体来说,批量归一化的过程如下: 计算均值和方差:对于每一层的输入,计算该层在一个小批量(batch)上的均值和方差。通常是在训练过程中,对每个特征(特征是指每一维数据)独立地计算均值和方差。 归一化:利用上述计算出的均值和方差,对输入数据进行归一化。每个输入的值减去该批量的均值并除以该批量的标准差,从而将输入的分布调整为均值为0,方差为1的标准正态分布。 缩放与偏移:归一化后的数据会通过一个可学习的参数进行缩放(scale)和偏移(shift),即引入两个新的参数:γ(gamma)和β(beta)。这些参数允许模型恢复某些可能丢失的信息。 简单理解批量归一化就是对输入的数据按照按照小批量的均值、方差、$\boldsymbol{\gamma}$和$\boldsymbol{\beta}$的公式进行处理,得到输出后的数据。这样也相当于对输入的数据加入了噪音,因此不要和丢弃法混合使用。 $$\mathrm{BN}(\mathbf{x}) = \boldsymbol{\gamma} \odot \frac{\mathbf{x} - \hat{\boldsymbol{\mu}}\mathcal{B}}{\hat{\boldsymbol{\sigma}}\mathcal{B}} + \boldsymbol{\beta}.$$ $\hat{\boldsymbol{\mu}}_\mathcal{B}$:是小批量 $\mathcal{B}$的样本均值 $\hat{\boldsymbol{\sigma}}_\mathcal{B}$:是小批量$\mathcal{B}$的样本标准差。 由于单位方差(与其他一些魔法数)是一个主观的选择,因此我们通常包含拉伸参数(scale)$\boldsymbol{\gamma}$和偏移参数(shift)$\boldsymbol{\beta}$,它们的形状与$\mathbf{x}$相同。需要注意的是,$\boldsymbol{\gamma}$和$\boldsymbol{\beta}$是需要与其他模型参数一起学习的参数。 由于在训练过程中,中间层的变化幅度不能过于剧烈,而批量规范化将每一层主动居中,并将它们重新调整为给定的平均值和大小。 如下所示: net = nn.Sequential( nn.Conv2d(1, 6, kernel_size=5), BatchNorm(6, num_dims=4), nn.Sigmoid(), nn.AvgPool2d(kernel_size=2, stride=2), nn.Conv2d(6, 16, kernel_size=5), BatchNorm(16, num_dims=4), nn.Sigmoid(), nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(), nn.Linear(16*4*4, 120), BatchNorm(120, num_dims=2), nn.Sigmoid(), nn.Linear(120, 84), BatchNorm(84, num_dims=2), nn.Sigmoid(), nn.Linear(84, 10)) 上面的示例中,在卷积层的后面使用了BatchNorm(6, num_dims=4)批量归一化。批量归一化就是固定小批量中的均值和方差,然后学习出适合的偏移和缩放,这样可以加速手链速度,但一般不改变模型的精度 残差网络ResNet 使用残差可以使得模型可以容易得叠加很多层,先来看看,什么是残差网络?残差网络就是由一系列的残差块组成,下图就是一个残差块。用公式表示就是:$X_{l+1} = X_l + F(X_l, W_l)$,,其中$F(X_l, W_l)$是残差。 残差块分有直接映射+残差两部分组成,表示输入经过残差块或直接映射到底输出。 在传统的神经网络中,输入$ X $会经过多层变换(如卷积、激活等),最终得出输出$ Y $。这些变换会逐渐改变输入的信息,试图将其转化为输出的目标形式。而在残差网络中,模型不仅学习输入$ X $到输出 $ Y $的映射,而是学习输入和输出之间的差异,即残差。数学上,可以表示为: $$ Y' = X + F(X) $$ 其中,$ Y' $是网络的最终输出,$ F(X) $ 是通过多个层(如卷积层、激活层等)处理后的结果(这个部分是“残差”),而 $ X $是输入。这里,$ F(X) $ 就是输入 $ X $与输出$ Y $之间的差异。也就是说X加上一个什么样的函数,能逼近Y。 为什么学习残差更容易? 学习从输入到输出的直接映射可能很复杂,特别是在深层网络中,因为输入经过多次变换后,最终的输出可能与输入有很大的差异。传统网络需要学习整个映射过程,这样可能导致训练时出现梯度消失或信息丢失的问题。但是,学习输入和输出之间的残差通常更简单。因为,通常情况下,输入和输出之间的差异(残差)可能是一个相对较小且较简单的函数。这使得网络能更容易捕捉到输入与输出之间的“偏差”,而不是直接学习整个变换过程。 举个例子 假设我们有一个非常深的网络,输入 $ X $ 和目标输出 $ Y $ 之间的关系很复杂。传统的网络可能需要直接学习一个非常复杂的映射函数。与此不同,残差网络并不直接学习这个复杂的映射,而是学习输入 $ X $ 和输出 $ Y $ 之间的差异。 例如,如果输出 $ Y $ 只是输入 $ X $ 加上一个小的偏差(例如,$ Y = X + \epsilon $),那么残差 $ F(X) = \epsilon $ 就是一个简单的学习目标。这个“差异”往往比直接学习整个映射来得容易。 可以把残差看作是一个补充信息。例如,假设你有一个图片分类任务,输入是图片,输出是类别标签。传统网络要直接将图片映射到标签,这个过程非常复杂。而在残差网络中,网络实际上在学习的是“这张图片与类别标签之间的差异”。如果输入与输出之间的关系可以通过一个小的差异来描述,那么网络只需要学习这个差异,训练起来会更容易。 残差网络的关键在于它将学习的重点从直接映射 $ X \to Y $ 转变为学习输入和输出之间的差异(残差) $ F(X) $。这样,网络不仅能更加高效地训练,还能避免深层网络中常见的梯度消失和信息衰减问题。 上图有两个残差块,左图中X可以直接到输出,右图中X经过1*1 Conv层到输出。对于左图当虚线框中的块如果是0,那么X还是原来的X。通过残差在在计算梯度时,可以使得接近输入层的参数可以得到更好的训练,因为经过多层神经网络后,最后一层可以通过“捷径”直到前面的层,这样梯度计算就更方便。 使用残差可以高效的训练靠近输入的神经网络的参数,避免层数的加深,越靠近输入的神经网络层参数变化较小而导致难以训练,因为梯度的计算是从后往前,而最后的参数如果相对较小时,通过链式法则计算(相乘)的前面梯度会更小,也就是前面层数w变化就小。 import torch from torch import nn from torch.nn import functional as F from d2l import torch as d2l class Residual(nn.Module): #@save def __init__(self, input_channels, num_channels, use_1x1conv=False, strides=1): super().__init__() self.conv1 = nn.Conv2d(input_channels, num_channels, kernel_size=3, padding=1, stride=strides) self.conv2 = nn.Conv2d(num_channels, num_channels, kernel_size=3, padding=1) if use_1x1conv: self.conv3 = nn.Conv2d(input_channels, num_channels, kernel_size=1, stride=strides) else: self.conv3 = None self.bn1 = nn.BatchNorm2d(num_channels) self.bn2 = nn.BatchNorm2d(num_channels) def forward(self, X): Y = F.relu(self.bn1(self.conv1(X))) Y = self.bn2(self.conv2(Y)) if self.conv3: X = self.conv3(X) Y += X #---------------->核心算法 return F.relu(Y) #构建一个残差块 def resnet_block(input_channels, num_channels, num_residuals, first_block=False): blk = [] for i in range(num_residuals): if i == 0 and not first_block: blk.append(Residual(input_channels, num_channels, use_1x1conv=True, strides=2)) else: blk.append(Residual(num_channels, num_channels)) return blk b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3), nn.BatchNorm2d(64), nn.ReLU(), nn.MaxPool2d(kernel_size=3, stride=2, padding=1)) #b2~b5是残差块生成 b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True)) b3 = nn.Sequential(*resnet_block(64, 128, 2)) b4 = nn.Sequential(*resnet_block(128, 256, 2)) b5 = nn.Sequential(*resnet_block(256, 512, 2)) net = nn.Sequential(b1, b2, b3, b4, b5, nn.AdaptiveAvgPool2d((1,1)), nn.Flatten(), nn.Linear(512, 10)) X = torch.rand(size=(1, 1, 224, 224)) for layer in net: X = layer(X) print(layer.__class__.__name__,'output shape:\t', X.shape) 运行结果: Sequential output shape: torch.Size([1, 64, 56, 56]) Sequential output shape: torch.Size([1, 64, 56, 56]) Sequential output shape: torch.Size([1, 128, 28, 28]) Sequential output shape: torch.Size([1, 256, 14, 14]) Sequential output shape: torch.Size([1, 512, 7, 7]) AdaptiveAvgPool2d output shape: torch.Size([1, 512, 1, 1]) Flatten output shape: torch.Size([1, 512]) Linear output shape: torch.Size([1, 10]) Sequential( (0): Sequential( (0): Conv2d(1, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3)) (1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) (2): ReLU() (3): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False) ) (1): Sequential( (0): Residual( (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) ) (1): Residual( (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) ) ) (2): Sequential( (0): Residual( (conv1): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1)) (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (conv3): Conv2d(64, 128, kernel_size=(1, 1), stride=(2, 2)) (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) ) (1): Residual( (conv1): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) ) ) (3): Sequential( (0): Residual( (conv1): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1)) (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (conv3): Conv2d(128, 256, kernel_size=(1, 1), stride=(2, 2)) (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) ) (1): Residual( (conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) ) ) (4): Sequential( (0): Residual( (conv1): Conv2d(256, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1)) (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (conv3): Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2)) (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) ) (1): Residual( (conv1): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) ) ) (5): AdaptiveAvgPool2d(output_size=(1, 1)) (6): Flatten(start_dim=1, end_dim=-1) (7): Linear(in_features=512, out_features=10, bias=True) ) 本文来自: <动手学深度学习 V2> 的学习笔记