sotfmax回归实现

什么是sotfmax回归

Softmax回归（Softmax Regression），也叫多项逻辑回归，是一种用于多分类问题的分类算法。它是对逻辑回归（Logistic Regression）的一种扩展，适用于处理输出类别数大于2的情况。Softmax回归通过使用Softmax函数来将每个类别的输出转化为一个概率分布，使得输出值能够表示每个类别的概率，并且所有类别的概率之和为1。

举个例子：假设有一个包含3个类别的多分类问题：苹果、香蕉、橙子。对于每个输入样本（例如一张图片），Softmax回归模型会输出三个值（每个类别的概率），也就是概率分布。例如：

• 苹果的概率：0.6
• 香蕉的概率：0.3
• 橙子的概率：0.1

这些概率加起来等于1，模型会将输入样本分类为苹果（因为概率最大）。

softmax函数

对于每个类别k ，我们会计算一个得分z_k，然后将这个得分转化为概率。得分通常是由输入数据\mathbf{x}与对应类别的权重向量\mathbf{w}_k 的线性组合给出的：z_k = \mathbf{w}_k^T \mathbf{x} + b_k, 其中，\mathbf{w}_k 是第k 个类别的权重，b_k 是偏置项，\mathbf{x} 是输入特征向量。Softmax函数用于将这些得分z_k转换成概率。

Softmax函数的形式如下：P(y = k | \mathbf{x}) = \frac{e^{z_k}}{\sum_{j=1}^K e^{z_j}} 。

• $ P(y = k | \mathbf{x}) ) 是输入 ( \mathbf{x} $ 属于类别k的概率。
• $ z_k $ 是类别 $ k $ 的得分。
• $ \sum_{j=1}^K e^{z_j} $ 是所有类别得分的指数函数的和，确保概率和为1。

交叉熵损失函数

为了训练Softmax回归模型，我们使用交叉熵损失函数来评估模型预测与真实标签之间的差异。交叉熵损失函数的公式如下：L(\theta) = - \sum_{i=1}^N \sum_{k=1}^K y_{ik} \log P(y_k = 1 | \mathbf{x}_i)

其中：
- N 是训练集中的样本数。
- y_{ik} 是样本 i是否属于类别 k 的标签（通常是1或0）。
- P(y_k = 1 | \mathbf{x}_i) 是输入 \mathbf{x}_i 属于类别 k 的概率。

softmax实现示例

数据读取

pip install d2l==0.16

import torch
from IPython import display
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

这里直接使用了d2l.load_data_fashion_mnist() 函数加载 Fashion-MNIST 数据集。load_data_fashion_mnist 是 d2l 库中的一个工具函数，用于加载 Fashion-MNIST 数据集并返回训练集和测试集的数据迭代器。train_iter 是训练集的迭代器。test_iter 是测试集的迭代器。数据迭代器是用于在模型训练和评估过程中批量加载数据的对象。batch_size 参数指定了每个批次包含多少个样本。

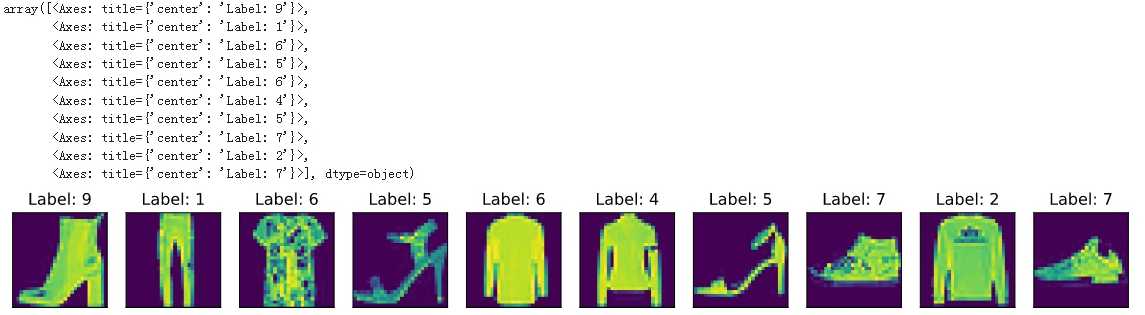
可以用下面的示例代码打印输入的数据

n = 10
for X, y in train_iter:
    break
X_selected = X[0:n].reshape((n, 28, 28))
titles = [f'Label: {int(label)}' for label in y[0:n]]
d2l.show_images(X_selected, 1, n, titles=titles)

定义模型

sotfmax函数

计算softmax的步骤如下：

• 对每个项求幂（使用exp）
• 对每一行求和（小批量中每个样本是一行），得到每个样本的规范化常数
• 将每一行除以其规范化常数，确保结果的和为1

def softmax(X):
    X_exp = torch.exp(X)
    print(X_exp)
    partition = X_exp.sum(1, keepdim=True)
    print(partition)
    return X_exp / partition

示例如下：

X = torch.normal(0, 1, (2, 5)) #使用正态分布生成2行5列的矩阵
print(X)
X_prob = softmax(X)
X_prob, X_prob.sum(1)

#生成的数据
tensor([[ 0.3141,  0.5186, -0.6949,  0.5918, -2.2370],
        [-0.3814,  0.8092, -0.1959,  0.7489,  1.8790]])

#torch.exp(X)：对矩阵中每个数据求e^x指数运算后的结果
tensor([[1.3690, 1.6797, 0.4991, 1.8072, 0.1068],
        [0.6829, 2.2460, 0.8221, 2.1146, 6.5472]])

#X_exp.sum(1, keepdim=True)： 对每一行求和
tensor([[ 5.4618],
        [12.4129]])

#将每一行除以其规范化常数，确保结果的和为1
(tensor([[0.2506, 0.3075, 0.0914, 0.3309, 0.0196],
         [0.0550, 0.1809, 0.0662, 0.1704, 0.5275]]),


tensor([1., 1.]))

模型和参数

num_inputs = 784
num_outputs = 10
W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True) b = torch.zeros(num_outputs, requires_grad=True)


def net(X):
    return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)

模型还是使用的是线性模式，只是在线性模型的基础上再加了一个softmax函数。模型的数学表示为：\hat{y} = \text{softmax}(X W + b)

• $ X \in \mathbb{R}^{n \times 784} $ 是输入样本矩阵，$ n $ 是样本数量。
• $ W \in \mathbb{R}^{784 \times 10} $ 是权重矩阵。
• $ b \in \mathbb{R}^{10} $ 是偏置向量。
• $ \hat{y} \in \mathbb{R}^{n \times 10} $ 是输出矩阵，其中每一行是一个样本的预测类别概率。

softmax 函数的公式为：\text{softmax}(z_i) = \frac{e^{z_i}}{\sum_{j} e^{z_j}}

其中 z_i 是某一类别的得分，j 遍历所有类别（在这个例子中是 10 个类别）。通过 softmax 函数，每个输出都会被转换为一个概率，所有类别的概率加起来为 1。

定义损失函数

def cross_entropy(y_hat, y):
    return - torch.log(y_hat[range(len(y_hat)), y])

• y_hat：这是模型的预测输出，通常是一个经过 softmax 函数处理的概率分布。y_hat 的形状通常是 (batch_size, num_classes)，其中 batch_size 是样本数量，num_classes 是类别数量。每一行表示一个样本对各个类别的预测概率。
• y：这是实际标签的索引，形状为 (batch_size,)，表示每个样本的真实类别的索引。
• y_hat[range(len(y_hat)), y]：这是通过 y 中的类别索引提取 y_hat 中对应类别的预测概率。range(len(y_hat)) 生成一个从 0 到 batch_size-1 的索引序列，表示每个样本。通过 y 索引，获取每个样本对应类别的概率值。
• torch.log(...)：对提取的预测概率取对数。交叉熵损失函数中有一个 log 操作，它衡量了预测概率和真实标签之间的差异。
• 负号：交叉熵是通过负对数似然（negative log-likelihood）计算的，因此需要对结果取负。

损失函数的公式为：L = - \frac{1}{n} \sum_{i=1}^{n} \log(\hat{y}_{i, y_i}), 通过对每个样本的预测概率取对数，并对所有样本的对数损失求和再取负值。

分类精度

分类精度= 样本预测正确数量除以样本总数（len(y)）。 也可以理解是预测对的概率，比如输入样本图片识别正确数为1，总样本数2时，精度为 1/2 = 0.5。

先看看例子，y_hat模型的预测输出，通常是一个二维矩阵，形状为 (样本数, 类别数)。例如，2个样本（输入的图片）3个类别(猫、狗、猪)的输出可能是 [[0.1, 0.2, 0.7], [0.3, 0.4, 0.3]]，即每个样本对应输出的一个概率分布，样本1对应的概率分布[0.1, 0.2, 0.7]，样本2对应的概率分布是[0.3, 0.4, 0.3]，而真实的标签y是一个一维向量，每个元素表示对应样本的正确类别索引，如[2, 1]，其中2代表的是狗，1代表猫。

那y_hat和y怎么做比较和转换了？
解决的办法就是，我们取每个样本概率分布中最大概率的索引，也就是通过 argmax(axis=1) 沿着行方向（即每个样本）找到概率最大的类别索引。例如，[[0.1, 0.2, 0.7], [0.3, 0.4, 0.3]] 会得到 [2, 1]， 即第一行最大是0.7，索引位置是2，第二行最大是0.4，级索引是1。有了这样的结果，就可以y_hat和y做比较了，比如y=[2,1], 那么y_hat输出结果是[2,1]，那么表示全部预测对。

def accuracy(y_hat, y):
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    #y_hat将输出索引如[2,1],下面结算的是y_hat和y进行比较，返回正确的个数。
    cmp = y_hat.type(y.dtype) == y
    return float(cmp.type(y.dtype).sum())

因此上面这个函数，最终返回的是正确的个数，比如y_hat = [[0.1, 0.2, 0.7], [0.3, 0.4, 0.3]],y是[2,2]经过accuracy函数处理后，返回的是结果是1， 因为y_hat = y_hat.argmax(axis=1)计算后，返回的是[2,1]，与实际的标签[2,2]有一个不对，即第二个样本预测错了。那么最终的分类精度就等于1/2 = 0.5。

训练

def train_epoch_ch3(net, train_iter, loss, updater):
    # 将模型设置为训练模式
    if isinstance(net, torch.nn.Module):
        net.train()
    # 训练损失总和、训练准确度总和、样本数
    metric = Accumulator(3)
    for X, y in train_iter:
        # 计算梯度并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad()
            l.mean().backward()
            updater.step()
        else:
            # 使用定制的优化器和损失函数
            l.sum().backward()
            updater(X.shape[0])
        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # 返回训练损失和训练精度
    return metric[0] / metric[2], metric[1] / metric[2]

def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):
    animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
                        legend=['train loss', 'train acc', 'test acc'])
    for epoch in range(num_epochs):
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
        //返回训练损失和训练精度
        test_acc = evaluate_accuracy(net, test_iter)
        //返回的是测试精度
        animator.add(epoch + 1, train_metrics + (test_acc,))
        //将其绘制到图像上。
    train_loss, train_acc = train_metrics
    assert train_loss < 0.5, train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc

lr = 0.1
def updater(batch_size):
    return d2l.sgd([W, b], lr, batch_size)

num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)

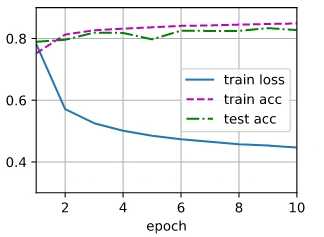
下面是训练的过程显示：

• train loss: 训练损失，也就是损失函数的结果。是模型在训练集上的平均损失值，通常使用损失函数来衡量。例如，常用的交叉熵损失（cross-entropy loss）或均方误差（mean squared error）。损失越小，说明模型在训练数据上的表现越好。它反映了模型预测值与真实标签之间的差距。
• train acc: Training Accuracy, 训练精度。是模型在训练集上的正确预测的比例。它通过比较模型的预测结果和真实标签来计算。训练精度=正确预测的样本数量/总样本数量。训练准确度越高，说明模型在训练数据上的拟合程度越好。训练准确度反映了模型对训练集的学习能力。
• test acc: Test Accuracy,测试精度。是指模型在未见过的测试集上的准确度。它与训练准确度不同，测试集用来评估模型的泛化能力。测试准确度反映了模型对新数据的预测能力。如果测试准确度高，说明模型不仅在训练集上表现好，而且具有较强的泛化能力，能够适应未见过的数据。

预测

def predict_ch3(net, test_iter, n=6):
    for X, y in test_iter:
        break
    trues = d2l.get_fashion_mnist_labels(y)
    preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
    titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
    d2l.show_images(
        X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])

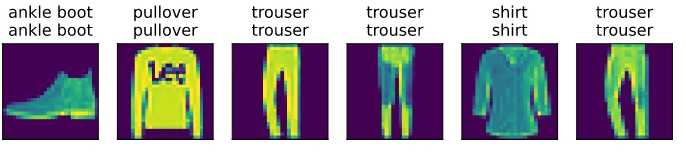
predict_ch3(net, test_iter)

使用训练好的模型，来预测实际的效果：

总结

一、公式和代码

公式：y = softmax(WX+b)
代码实现：y = softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)

二、输入和输出示例

输入：
X= torch.Size([256, 1, 28, 28])-->X=torch.Size([256, 784])
由于WX要满足矩阵乘，所以要把X做处理X.reshape((-1, W.shape[0]))

W=torch.Size([784, 10])
b=torch.Size([10])

输出:

y_hat=torch.Size([256, 10])   -->([256,784])*([784,10]) = ([256, 10])矩阵相乘

下面是打印第一行的结果，也就是对应输入第一个样本的预测结果。 最后为0.99613，如果最后一项是代表是shirt，但是表示第一个样本就是shirt。
tensor([4.8291e-06, 1.2489e-07, 3.7127e-06, 2.1127e-07, 1.3334e-06, 2.6440e-03,
        1.9091e-05, 8.7211e-04, 3.2460e-04, 9.9613e-01])