激活函数

概念

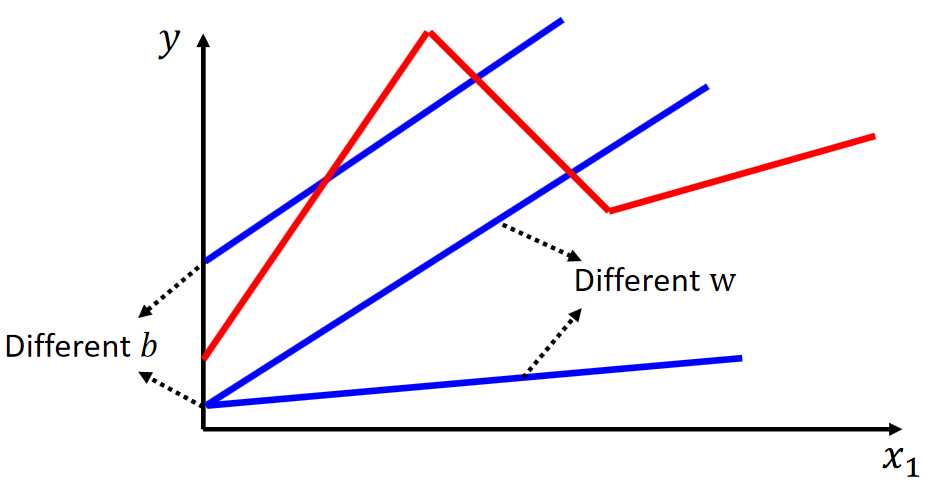
前面我们主要使用的是线性模型，但是线性模型有很多局限性，因为我们要建模的问题并不能单纯使用线性模型就能够拟合的，如下示例。

我们要拟合红色部分的函数，使用线性模型即使在怎么调整W和b都没法进行拟合出来，要拟合这样的函数，我们需要非线性的函数。

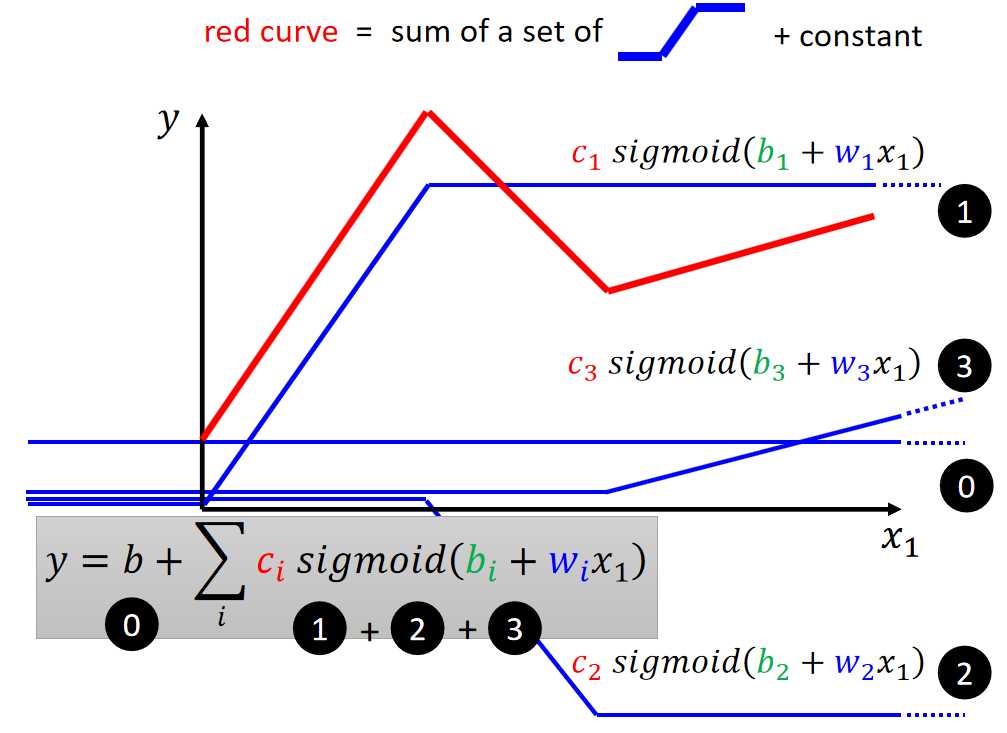
如上图，要拟合这样的模型，我们可以使用①②③函数相加再加上一个b偏置。那这里的①②③函数怎么来了，可以看出是wx+b再经过一个sigmoid转换得来，那这里的sigmoid我们就称为激活函数。

激活函数的主要作用是引入非线性，使得神经网络能够处理更复杂的问题并避免退化成线性模型。没有激活函数，神经网络就无法发挥其强大的学习和表达能力。选择合适的激活函数对模型的训练和性能表现至关重要。

常见的激活函数

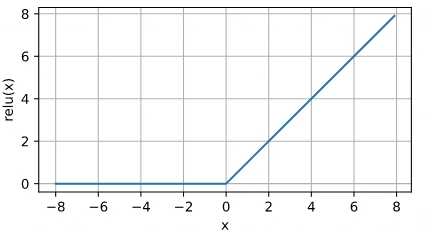
ReLU 激活函数

公式：\text{ReLU}(x) = \max(0, x)

x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.relu(x)
d2l.plot(x.detach(), y.detach(), 'x', 'relu(x)', figsize=(5, 2.5))

ReLU激活函数用得比较多，因为其计算相对简单，不需要复杂的指数计算，因为指数计算都很贵。

ReLU函数进行求导，可以发现当输入为负时，导数为0，当输入为正是，导数为1。可以使用y.backward来计算导数，可以理解导数就是梯度。x取不同位置进行求导得到的值，就是相应位置的梯度。

y.backward(torch.ones_like(x), retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of relu', figsize=(5, 2.5))

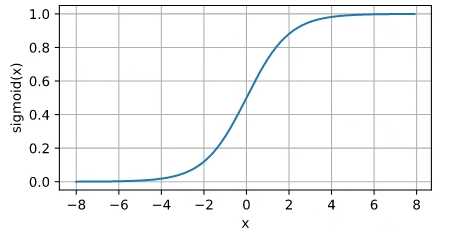
Sigmoid 激活函数

公式： \sigma(x) = \frac{1}{1 + e^{-x}}

y = torch.sigmoid(x)
d2l.plot(x.detach(), y.detach(), 'x', 'sigmoid(x)', figsize=(5, 2.5))

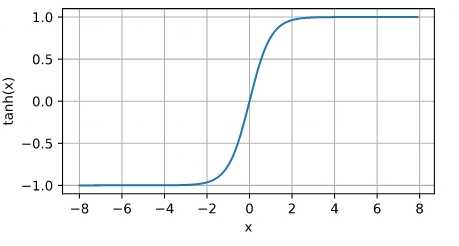
Tanh 激活函数

公式： \tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}

y = torch.tanh(x)
d2l.plot(x.detach(), y.detach(), 'x', 'tanh(x)', figsize=(5, 2.5))

Softmax 激活函数

公式： \text{Softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{K} e^{z_j}}

在前面章节中，我们使用softmax用于线性回归的多分类，但其实softmax也可以看做一种激活函数。
softmax将神经网络的输出转换为概率分布，确保每个类别的输出值在0到1之间，且所有类别的概率和为1。如z=[2.0,1.0,0.1] 经过softmax计算转化后得[0.7,0.2,0.1]，如果神经网络的输出为三个类别的得分，表示第一个类别的预测概率最大，约为70

总结来说，Softmax 是一种激活函数，它专门用于多分类问题的输出层，帮助模型生成一个概率分布，便于做分类决策。