全连接层与卷积层参数计算

层的概念

在前面https://www.laumy.tech/2013.html有说明"层与块"概念，为了加深影响，本章再简要概括一下深度学习中常见的层。

在深度学习中，层（Layer)是神经网络的基本构建模块，负责对输入数据进行特定变换（如线性加权、非线性激活、特征提取等）。每一层接收输入数据，通过内部参数和计算规则生成输出，传递给下一层。常见的层有全连接层、激活函数层、卷积层、池化层、归一化层（Normalization Layer）、正则化（dropout）。当然层还可以自己定义。

全连接层

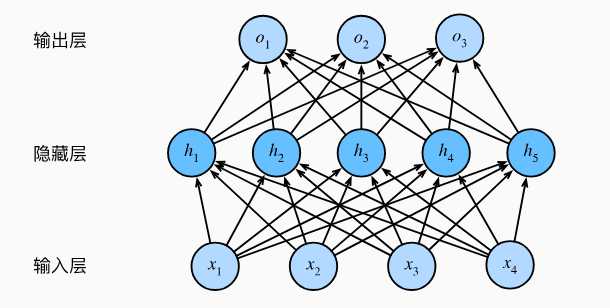
全连接层（Fully Connected Layer）是指当前层每个神经元均与前一层的所有神经元相，通过权重矩阵和偏置向量实现全局特征整合。全连接层计算公式为y=wx+b。其作用是将局部特征（如卷积层提取的边缘、纹理）映射为全局语义信息（如物体类别），常用于分类或回归任务的输出层。

下面是一个全连接层的结构。从上面的结构可以总结一下全连接层的参数计算公式，Params=(输入节点+1）×输出节点数,公式中的+1代表的是偏置项（bias）。

因此上图中的总参数量为：（4+1）*5 + (5+1)*3 = 25 + 18 = 43。

卷积层

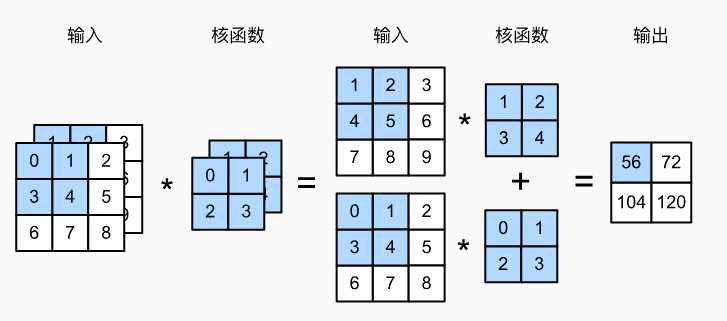
卷积核是在输入数据上滑动，计算局部区域的加权和（如3×3窗口），其作用可以捕边缘、纹理、形态等基础特征。

卷积核的参数计算公式为，参数量=(卷积核高×卷积核宽×输入通道数+1)×输出通道数。上图示例中，输入2通道，输出1通道，所以参数量为2*2*2*1 = 8,这里没有考虑偏置bias。从这里可以看出，相对卷积层比全连接层参数很少很多。