优化算法

局部最小与全局最小

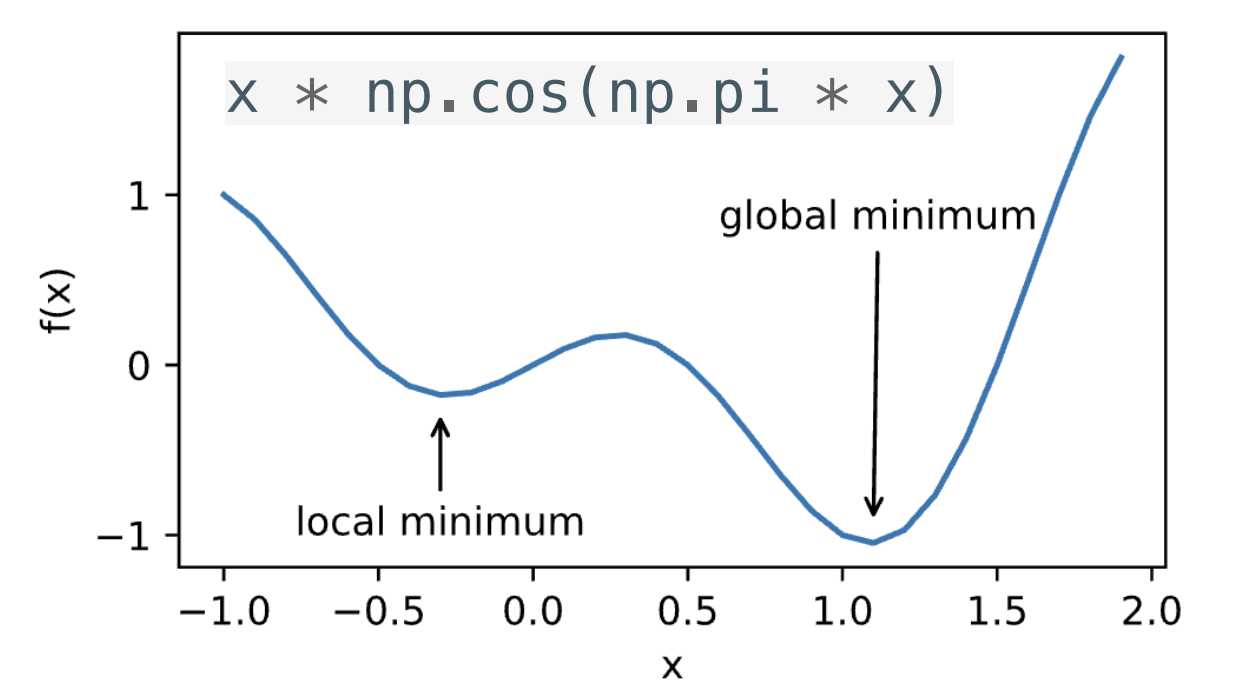
对应任何目标函数f(x)，当然这里的目标函数可以是损失函数。如果在x处对应的f(x)小于x附近任意点的f(x)，那么f(x)是局部最小的。如果f(x)在x处的值是整个域中目标函数的最小值，那么f(x)是全局最小值。

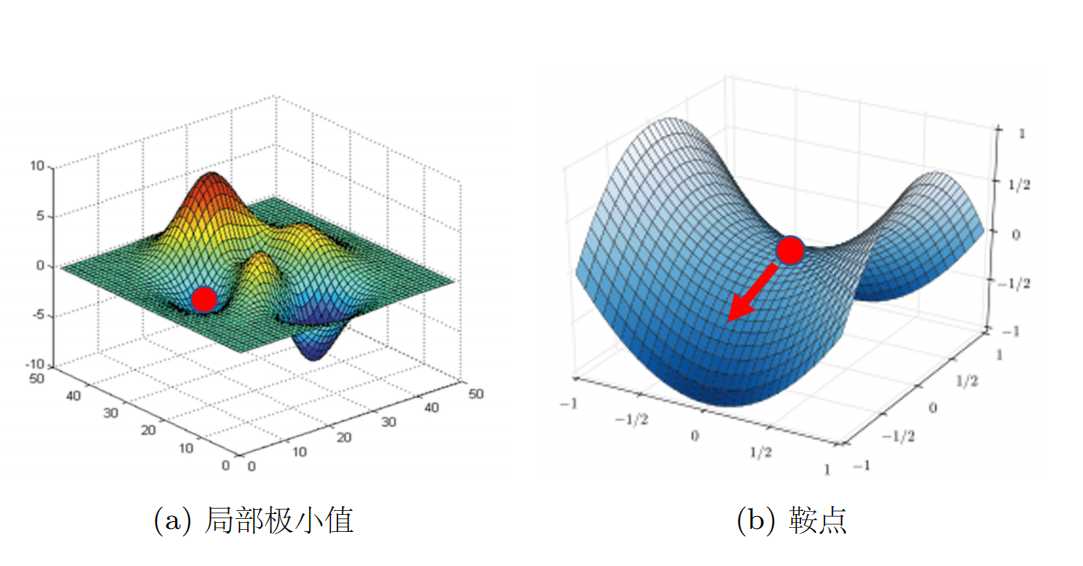
除了局部最优解外，鞍点也是梯度为0的区域。什么是鞍点了？如下图。

在深度学习模型训练中，通常往往会有许多局部最优解或鞍点，要解决这种局部最优解需要一定程度的噪音才能使参数跳出局部最小值，实际上使用小批量随机梯度下降也可以将参数从局部极小值中跳出。

梯度下降(gd)

对于多变量的输入\mathbf{x} = [x_1, x_2, \ldots, x_d]^\top的情况。它的梯度也是多元的，是一个由d个偏导数组成的向量：

\nabla f(\mathbf{x}) = \bigg[\frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \ldots, \frac{\partial f(\mathbf{x})}{\partial x_d}\bigg]^\top

梯度中的每个偏导数元素\partial f(\mathbf{x})/\partial x_i代表了当输入x_i时f在\mathbf{x}处的变化率。最陡下降的方向由负梯度-\nabla f(\mathbf{x})得出。选择合适的学习率\eta > 0来生成典型的梯度下降算法：

\mathbf{x} \leftarrow \mathbf{x} - \eta \nabla f(\mathbf{x})

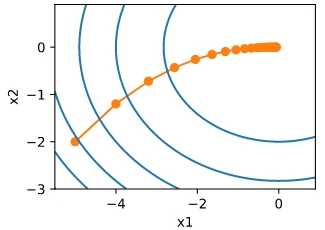
假设一个目标函数f(\mathbf{x})=x_1^2+2x_2^2，并有二维向量\mathbf{x} = [x_1, x_2]^\top作为输入，标量作为输出。则梯度\nabla f(\mathbf{x}) = [2x_1, 4x_2]^\top给出。下面是梯度从[-5,-2]开始进行下降。

注意，在实际训练时，如果f(x)是损失函数，那么x就是参数，通常对应的是w。

随机梯度下降(sgd)

在深度学习中，在训练数据时，有很多样本，按照前面的梯度下降方法，那么对于多个样本的损失我们可以使用平均值来表示。给定n个样本的训练数据集，我们假设f_i(\mathbf{w})是关于索引i的训练样本的损失函数，其中\mathbf{w}是参数向量，我们得到损失函数为：

f(\mathbf{w}) = \frac{1}{n} \sum_{i = 1}^n f_i(\mathbf{w})

\mathbf{w}的目标函数的梯度计算为

\nabla f(\mathbf{w}) = \frac{1}{n} \sum_{i = 1}^n \nabla f_i(\mathbf{w})

如果使用梯度下降法，每计算一次梯度，需要对所有的样本做计算求平均，如果每个自变量迭代的计算代价为\mathcal{O}(n)，它随n线性增长。这样的方法虽然计算梯度准确性高，但是当训练数据集较大时，每次迭代的梯度下降计算代价将较高。

随机梯度下降（SGD）就是要降低计算量，在计算梯度时，不要对所有样本进行计算，而是在随机梯度下降的每次迭代中，对数据样本随机均匀采样一个索引i，也就是只取一个样本计算计算梯度， 其中i\in{1,\ldots, n}，并计算梯度\nabla f_i(\mathbf{w})以更新\mathbf{w}：

\mathbf{w} \leftarrow \mathbf{w} - \eta \nabla f_i(\mathbf{w}),

其中\eta是学习率。可以看到，每次迭代的计算代价从梯度下降的\mathcal{O}(n)降至常数\mathcal{O}(1)。此外，我们要强调，随机梯度\nabla f_i(\mathbf{w})是对完整梯度\nabla f(\mathbf{w})的无偏估计，因为

\mathbb{E}_i \nabla f_i(\mathbf{w}) = \frac{1}{n} \sum_{i = 1}^n \nabla f_i(\mathbf{w}) = \nabla f(\mathbf{w}).

这意味着，平均而言，随机梯度是对梯度的良好估计。

总结一下，梯度下降使用全量数据计算梯度更新参数，适合小数据集，而随机梯度下降每次使用一个样本更新，适合大数据集。

小批量随机梯度下降(minibatch-sgd)

使用随机梯度下降只取一个样本，虽然降低了计算难度，但是如果样本差异较大时梯度波动大，收敛不稳定，而且不能做并行计算。对梯度下降和随机梯度下降做一个折中，对于批量输入样本，我们分为多个小批量，计算梯度是我们使用小批量来计算梯度，这样相对梯度下降不是算全部，同时对于如果是多GPU并行计算的，多个小批量可以并行，

(w, b) \leftarrow (w, b) - \frac{\eta}{|B|} \sum_{i \in B} \nabla_{(w, b)} \ell^{(i)}(w, b)

公式中的B是抽样的小批量，是固定数量的训练样本。梯度公式也可以表示为如下，其中Xi是第i个输入样本，W是参数：

\mathbf{g}_{t, t-1} = \frac{\partial \mathbf{W}}{|\mathcal{B}_t|} \sum_{i \in \mathcal{B}_t} f(\mathbf{X}_{i}, \mathbf{W}_{t-1})

总结一下，梯度下降使用全量数据更新参数，随机梯度下降每次使用一个样本更新，而小批量随机梯度下降则每次使用一小部分样本更新，介于二者之间。

动量法(momentum)

动量法是深度学习中一种常用的参数优化方法，旨在加速梯度下降优化过程，特别是在处理高维数据时能够帮助模型更快地收敛。其核心思想借鉴了物理中的动量概念，目的是避免在梯度下降过程中由于局部震荡而导致的效率低下。

在标准的梯度下降中，更新参数的方式是直接沿着梯度的方向调整参数：

w_t = w_{t-1} - \eta \nabla_w L(w_{t-1})

其中：
- w_t 是当前的参数，
- \eta 是学习率，
- \nabla_w L(w_{t-1}) 是当前参数的梯度。

动量法的思想是，不仅考虑当前的梯度，还要考虑前几次更新的方向和大小，从而引入“惯性”来加速优化过程，避免参数更新过程中出现震荡。具体的更新规则如下：

首先，计算当前参数的梯度：

\nabla_w L(w)

引入一个速度变量（momentum），根据上一次的速度和当前的梯度来计算新的速度：

v_t = \beta v_{t-1} + (1 - \beta) \nabla_w L(w)

其中：
- \beta 是动量衰减因子，通常取值在 [0, 1) 之间，表示前一次更新的影响程度，
- v_t 是当前的“速度”，表示参数更新的方向和大小。

用速度来更新参数：

w_t = w_{t-1} - \eta v_t

其中：
- \eta 是学习率，控制更新的步长。

动量法有什么效果了？

• 加速收敛：动量法能够加速收敛过程，特别是在处理高维数据时，能够减少梯度下降中震荡的现象。
• 克服局部最小值：动量法有助于跳出局部最小值，帮助优化算法在复杂的损失函数中找到更优的解。
• 提高稳定性：动量法通过结合前几次的梯度信息，使得参数更新更平滑，避免了仅依赖当前梯度时可能出现的震荡。

动量法有什么不足？

• 参数选择：动量法的效果在不同任务中依赖于动量衰减因子 \beta 和学习率 \eta 的选择，可能需要多次调参才能找到最优的参数。
• 计算开销：相比于标准的梯度下降，动量法需要额外保存上一次的梯度信息，因此增加了一定的内存开销。

常见的动量法变种？

• Nesterov Accelerated Gradient (NAG)：NAG 是动量法的一种改进方法，它在计算梯度时会考虑当前的速度，以更好地调整更新方向。
• 自适应动量法（Adam）：Adam 优化器结合了动量法和自适应学习率的方法，广泛用于深度学习中，能够自动调整每个参数的学习率。

总结下，动量法是深度学习中常见的优化算法，通过引入前几次梯度的加权平均，帮助加速收敛，减少震荡，并有效地应对复杂的损失函数。在实际应用中，动量法常常和其他优化方法结合使用，如自适应学习率方法（Adam）等。

Adam

adam是在动量法的基础上再加上自适应学习率，所谓自适应学习率就是根据历史梯队信息动态的调整。 想象一下你正在穿越一个复杂的地形，找到最低点，在道路平坦的地方你可以迈出大步，崎岖的地方减速这就是自适应调整学习率，同时你又保持一个动量，在你下一次动作时会有上一次的冲量，当转弯时会有上一次的动量也不至于一下偏差很远而错过。

Adam优化器通过计算梯度的一阶矩（即梯度的平均值）和二阶矩（即梯度的平方的平均值）来动态调整每个参数的学习率。具体的步骤如下：

首先计算一阶矩和二阶矩，对于每个参数w，Adam维护两个变量：

• 一阶矩 m_t（动量）：梯度的指数加权平均。
• 二阶矩v_t（自适应学习率）：梯度的平方的指数加权平均。

这两个变量分别更新如下：

m_t = \beta_1 m_{t-1} + (1 - \beta_1) \nabla_w L(w)

v_t = \beta_2 v_{t-1} + (1 - \beta_2) (\nabla_w L(w))^2

• $\nabla_w L(w)$ 是当前参数的梯度，
• $\beta_1$和 $\beta_2$是控制一阶矩和二阶矩衰减率的超参数，通常取值为 0.9 和 0.999。

由于在初始阶段一阶矩和二阶矩的估计偏向于零，Adam对这两个矩进行偏差修正：\hat{m_t} = \frac{m_t}{1 - \beta_1^t},\hat{v_t} = \frac{v_t}{1 - \beta_2^t}

最后，使用修正后的矩估计来更新参数：w_t = w_{t-1} - \eta \frac{\hat{m_t}}{\sqrt{\hat{v_t}} + \epsilon}。

• $\eta$是学习率，
• $\epsilon$ 是一个小常数（如 $10^{-8}$），用来避免除以零的情况。

Adam有什么优点？

• 自适应学习率：Adam会自动调整每个参数的学习率，这样可以在训练过程中避免手动调整学习率的麻烦。
• 结合了动量法和自适应学习率：通过一阶矩和二阶矩的估计，Adam能够更有效地处理不同参数在训练过程中的变化，避免了梯度下降过程中出现的震荡。
• 适用于大规模数据和高维参数：Adam能够在处理大规模数据时稳定并高效地收敛，特别是在处理稀疏梯度（如自然语言处理任务）时表现尤为突出。

Adam有什么缺点？

• 超参数调整：尽管Adam是自适应的，但在某些情况下，仍然需要调整超参数（如学习率 \eta，\beta_1 和 \beta_2）才能获得最好的训练效果。
• 可能导致过度拟合：在某些任务中，使用Adam优化器可能会导致模型的过度拟合，需要适当的正则化策略来避免。

Adam优化器通过结合动量法和自适应学习率调整的机制，能够加速模型训练过程，提高收敛速度，尤其适用于处理大规模数据和复杂的深度学习模型。